Продолжение. См. № 1, 3, 5, 7, 9, 15, 17/05
1 Деревянный куб с ребром длиной a = 10 см закреплён так, что одна из его вершин находится на горизонтальной плоскости, а центр куба лежит на одной вертикали с этой вершиной. Сверху на куб вертикально падает широкий параллельный пучок света. Определите площадь тени S, которую куб отбрасывает на горизонтальную плоскость. Дифракцией света пренебречь.
Решение
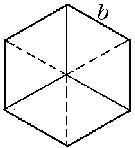
Вид на куб сверху показан на рисунке. Тень от куба представляет собой правильный шестиугольник со стороной b, равной расстоянию от боковой вершины куба до вертикали. Площадь тени равна
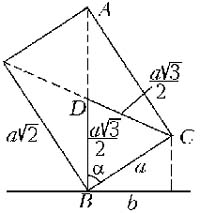
Для вычисления b рассмотрим сечение
куба вертикальной плоскостью, проходящей по
диагоналям двух его противоположных граней (AB –
вертикаль, BC – ребро куба, D – центр куба). Из
рисунка видно, что b = asin 
. По теореме косинусов, записанной для 
, имеем:
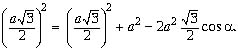
Отсюда 
Следовательно:
и 
Окончательно получаем: 
2 На
цилиндрическое зеркало, поперечное сечение
которого представляет собой полуокружность,
направили параллельно оси 
и симметрично относительно неё
параллельный пучок света, ширина которого равна
радиусу зеркала. Найдите наибольший угол 
между лучами
света, отражённого от зеркала.
Решение
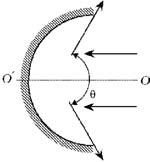
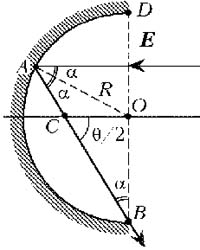
Рассмотрим ход крайнего луча,
образующего пучок, который изображён на рисунке.
Этот луч перпендикулярен диаметру BD, проходящему
через крайние точки зеркала. Угол падения этого
луча на зеркало (
, где O – центр зеркала, A – точка падения
луча), по условию задачи, равен = arcsin0,5 = 30°. По закону отражения, 
Тогда
отражённый луч пересекает прямую BD под углом 90°
– 2 = 30°, а
значит, точка их пересечения удалена от точки О
на расстояние R, т.е. совпадает с точкой B.
Следовательно, при падении на зеркало крайних
лучей из пучка отражённые лучи проходят через
край зеркала. Эти лучи расходятся под наибольшим
углом. Искомый угол расхождения лучей равен
удвоенному углу OCB, т.е. 
3 На
поверхность зеркального шара падают два
параллельных луча света, лежащие в плоскости,
проходящей через его центр. Расстояние между
лучами a=1см. Известно, что при отражении от
поверхности шара один из лучей отклоняется от
первоначального направления на угол =90°, а другой – на угол 
=60°. Найдите
радиус шара R.
Решение
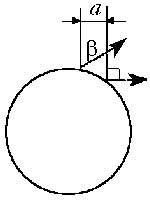
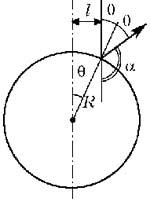
Ход луча, падающего на шар на некотором
расстоянии l от оси, параллельной лучу и
проходящей через центр шара, изображён на
рисунке, где –
угол падения,
– угол отклонения луча от первоначального
направления. Видно, что 
Отсюда получаем формулу, связывающую
расстояние l от луча до оси и угол отклонения луча:
Из этой формулы следует, что заданное в условии расстояние между двумя параллельными лучами, падающими на шар, выражается как
Отсюда получаем
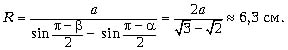
4
Плоскопараллельная пластинка толщиной d = 1 мм
изготовлена из прозрачной пластмассы
(показатель преломления n = 1,5). Изгибая пластинку,
ей придают форму, изображённую на рисунке, где
показано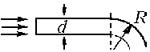 
поперечное сечение пластинки.
Перпендикулярно торцу пластинки на него падает в
плоскости рисунка параллельный пучок света.
Определите минимально допустимый радиус
кривизны Rmin изгиба пластинки, при котором свет не
будет выходить из пластинки через её боковую
поверхность. Радиус кривизны следует определять
по внешней (по отношению к направлению изгиба)
поверхности пластинки.
Решение
Рассмотрим ход светового луча,
распространяющегося вплотную к внутренней
поверхности плоской части пластинки. Легко
видеть, что из всех лучей, попавших внутрь
пластинки через её торец, этот луч имеет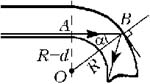 
наименьший угол падения на искривлённую поверхность
пластинки. Рассматриваемый луч не выйдет наружу,
если он испытает на искривлённой поверхности
полное отражение, условие которого имеет вид:
Ясно, что при выполнении этого условия
все остальные лучи, образующие пучок, также не
выйдут из пластинки через её искривлённую
поверхность. Из рисунка видно, что 
Объединяя записанные
соотношения, получаем ответ:
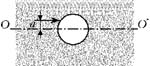
5 В толще
стекла (показатель преломления n = 1,5) имеется
сферическая полость, заполненная воздухом. Луч
света, распространяющийся в стекле, падает на
полость на малом расстоянии a от оси , проходящей через центр
полости параллельно лучу. На каком расстоянии b
от этой оси находится точка выхода луча из
полости? Углы падения и преломления считать
малыми.
Решение
Ход луча изображён на рисунке, где
через и обозначены
соответственно углы падения и преломления на
границе стекло–воздух. По закону преломления, 
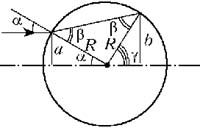
Из рисунка видно, что 
По условию задачи, углы и малы, следовательно, мал также и угол 
. Поэтому
справедливы приближённые равенства: 
Отсюда 
Тогда 