Продолжение. См. № 1, 3, 5, 7, 9/05
1 На плоской
горизонтальной непроводящей шероховатой
поверхности закреплён маленький шарик, имеющий
заряд q. Маленький брусок массой m,
несущий такой же по знаку и величине заряд,
помещают на эту поверхность на расстоянии l0
от закреплённого заряженного шарика. Какой путь l
пройдёт брусок до остановки, если его отпустить
без начальной скорости? Коэффициент трения между
бруском и поверхностью . Поляризацией материала
поверхности пренебречь. Электрическая
постоянная
0, ускорение свободного падения g.
Решение
Поскольку сила кулоновского взаимодействия между заряженными телами является потенциальной, для решения задачи можно воспользоваться законом изменения механической энергии. По условию, в начальном и конечном состояниях брусок неподвижен и его кинетическая энергия равна нулю. Следовательно, изменение потенциальной энергии взаимодействия зарядов равно работе силы трения на перемещении бруска из начального положения в конечное:
![]()
Отсюда находим ![]()
Необходимо иметь в виду, что этот результат справедлив не всегда. В самом деле, если в начальном положении бруска сила кулоновского отталкивания меньше максимального значения силы трения покоя, т.е.
![]()
то брусок в движение не придёт. Поэтому полная формулировка ответа такова:
![]() при
при ![]()
l = 0, при ![]()
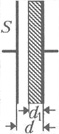
2 В плоском
воздушном конденсаторе к одной из обкладок
придвинута вплотную пластинка слюды толщиной
d1=0,3 мм. Диэлектрическая проницаемость
слюды = 7, площадь обкладок конденсатора S=200
см2, расстояние между ними d=0,5 мм.
Определите ёмкость конденсатора. Краевыми
эффектами пренебречь. Электрическая постоянная
0
= 8,85•10–12 Ф/м.
Решение
Поверхность слюды, обращённая к левой обкладке конденсатора, является эквипотенциальной, т.к. напряжённость электрического поля перпендикулярна ей. Нанесём мысленно на эту поверхность тонкий проводящий слой. При этом потенциал поверхности останется тем же самым и разность потенциалов между обкладками конденсатора не изменится. Поэтому не изменится и ёмкость конденсатора. Следовательно, конденсатор с диэлектрической пластинкой можно рассматривать как два последовательно соединённых конденсатора ёмкостями
![]() и
и ![]()
Окончательно
![]()
3 Плоский
конденсатор представляет собой две параллельные
металлические пластины, жёстко скреплённые
между собой изолирующими стержнями. Конденсатор
находится в вакууме и покоится на горизонтальной
подставке. Между пластинами конденсатора
распространяется пучок электронов, скорость
которых 0 направлена горизонтально. На
какую величину
![]() N изменится сила реакции подставки,
если на конденсатор подать напряжение, при
котором пучок на выходе из конденсатора
отклонится от первоначального направления на
угол
N изменится сила реакции подставки,
если на конденсатор подать напряжение, при
котором пучок на выходе из конденсатора
отклонится от первоначального направления на
угол ? Поле конденсатора считать однородным,
действием силы тяжести на электроны пренебречь.
Поперечное сечение пучка и концентрация
электронов в пучке на входе в конденсатор равны
соответственно S и n. Масса электрона m.

Решение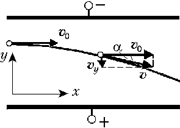
Поскольку электрическое поле внутри
конденсатора однородно и направлено
перпендикулярно его пластинам, а вне его равно
нулю, при пролёте конденсатора будет изменяться
только поперечная составляющая скорости
электронов, причём на выходе из конденсатора y=
0tg
. Следовательно, изменение импульса
одного электрона за время пролёта конденсатора
равно (в проекции на ось Y)
![]()
С другой стороны, по закону изменения
импульса, ![]() где F1 – проекция на ось Y
силы, действующей на электрон со стороны поля
конденсатора,
где F1 – проекция на ось Y
силы, действующей на электрон со стороны поля
конденсатора, ![]() t
– время пролёта конденсатора. Обозначив через l
длину пластин конденсатора, находим, что
t
– время пролёта конденсатора. Обозначив через l
длину пластин конденсатора, находим, что ![]() и
и ![]()
Одновременно в конденсаторе находятся
![]() электронов. Поэтому полная сила, действующая на
пучок, равна
электронов. Поэтому полная сила, действующая на
пучок, равна ![]()
По третьему закону Ньютона, искомая величина |![]() N| = |F|.
Поэтому окончательно
N| = |F|.
Поэтому окончательно ![]()
В зависимости от полярности
напряжения на конденсаторе пучок будет
отклоняться либо вверх (![]() ), либо вниз (
), либо вниз ( > 0). В
соответствии с этим сила реакции подставки будет
либо увеличиваться, либо уменьшаться на величину
|
![]() N|.
N|.
4
Непроводящая трубка, открытая с обоих концов,
расположена горизонтально. В трубке находятся
два металлических поршня площадью S каждый,
способные перемещаться без трения. Пространство
между поршнями заполнено воздухом при
атмосферном давлении, причём расстояние между
поршнями мало по сравнению с их диаметром. Во
сколько раз n уменьшится расстояние между
поршнями, если зарядить их разноимёнными
зарядами q и –q? Температура воздуха
постоянна. Атмосферное давление p0.
Электрическое поле между поршнями считать
однородным. Поляризацией материала трубки
пренебречь. Электрическая постоянная 0.
Решение
Обозначим через l0 и l
расстояния между поршнями до и после сообщения
им зарядов. Напряжённость поля, создаваемого
одним из поршней, равна ![]()
Поэтому величина силы электростатического притяжения между поршнями равна
![]()
Под действием этой силы поршни переместятся и займут новое положение равновесия. Обозначив через p давление воздуха в пространстве между поршнями после их зарядки, запишем условие равновесия каждого из поршней:
![]()
Поскольку температура воздуха постоянна, справедлив закон Бойля–Мариотта, согласно которому
![]()
Объединяя записанные выражения, получаем
ответ: ![]()