=
45°, а верёвка перпендикулярна лестнице. Центр
тяжести лестницы находится посередине.
Ускорение свободного падения принять равным g=10
м/с2.Продолжение. См. № 3, 5/05
10
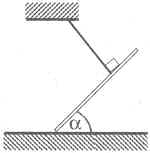
Лестница массой m=30 кг удерживается в
наклонном положении лёгкой нерастяжимой
верёвкой. Верёвка привязана к лестнице в точке,
отстоящей от верхнего конца лестницы на
расстояние, равное 1/3 длины лестницы. Найдите
величину силы нормального давления N
лестницы на пол, если лестница составляет с полом
угол =
45°, а верёвка перпендикулярна лестнице. Центр
тяжести лестницы находится посередине.
Ускорение свободного падения принять равным g=10
м/с2.
Решение
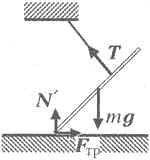
Лестница находится в равновесии под действием сил, указанных на рисунке, где через mg обозначена сила тяжести, через T – сила натяжения верёвки, через Fтр – сила трения, а через N' – нормальная составляющая реакции пола. Запишем условия равновесия лестницы в виде равенства нулю: 1) суммы сил в проекции на вертикальное направление; 2) суммы моментов сил относительно оси, перпендикулярной плоскости рисунка и проходящей через точку соприкосновения лестницы с полом:
Здесь L – длина лестницы. Исключая
из этих уравнений T, находим 
По третьему закону
Ньютона, искомая величина силы нормального
давления лестницы на пол N = N'. Получаем
11
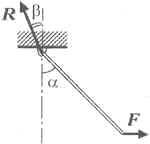
Однородный стержень может вращаться без трения
вокруг горизонтальной оси, проходящей через его
конец. К другому концу стержня приложена сила,
направленная горизонтально и перпендикулярно
оси вращения стержня. Под действием этой силы
стержень отклонён от вертикали на угол = 45°. Какой угол 
составляет
с вертикалью сила, действующая на стержень со
стороны оси?
Решение
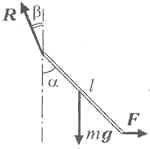
Стержень находится в равновесии под действием сил, изображённых на рисунке, где через mg обозначена сила тяжести (m – масса стержня), через F – сила, приложенная к стержню, а через R – сила реакции оси. Из условий равновесия вытекают следующие равенства:
Исключая отсюда F, R и mg, находим, что
Окончательно:
12
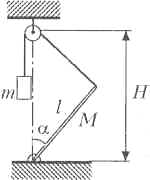
Однородный стержень массой M = 28 кг и длиной l=1,73
м закреплён нижним концом на шарнире. К верхнему
концу стержня привязана лёгкая нерастяжимая
верёвка, перекинутая через блок, укреплённый на
высоте H=2 м от шарнира на одной вертикали с
ним. Найдите массу m груза, который нужно
подвесить на другом конце верёвки, чтобы
стержень находился в равновесии, составляя угол = 30° с
вертикалью. Трением в шарнире и в блоке
пренебречь. Диаметр блока считать очень малым.
Решение
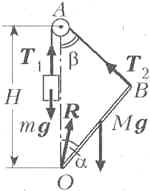
Система находится в равновесии под действием сил, изображённых на рисунке, где через mg и Mg обозначены силы тяжести, через T – сила натяжения верёвки, а через R – сила реакции шарнира. Из условия равновесия груза следует, что T1 = Т2 = Т = mg. Для описания равновесия стержня воспользуемся уравнением моментов относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O:
Отсюда
Из теоремы синусов, записанной для 
AOB,
следует равенство
По теореме косинусов для того же треугольника
Объединяя записанные выражения, получаем
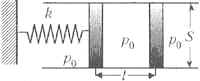
1 Горизонтальная трубка сечением S, открытая с двух концов, закреплена неподвижно. В ней находятся два поршня, один из которых соединён пружиной жёсткостью k с неподвижной стенкой. В исходном состоянии давление воздуха между поршнями равно атмосферному давлению p0, пружина не деформирована, расстояние между поршнями равно l. Правый поршень медленно переместили вправо на расстояние l. Какое давление воздуха p1 установилось при этом между поршнями? Температуру воздуха считать постоянной, трением пренебречь.
Решение
При перемещении правого поршня вправо на расстояние l левый поршень переместится в ту же сторону на некоторое расстояние x. Условие равновесия левого поршня имеет вид:
Отсюда давление воздуха между поршнями
Из закона Бойля–Мариотта следует равенство
Исключая из этих соотношений x, получаем квадратное уравнение относительно p1:
Выбирая положительный корень этого уравнения, получаем ответ:
