Продолжение. См. № 46/04

С.С.Чесноков, С.Ю.Никитин, И.П.Николаев,
Н.Б.Подымова, М.С.Полякова, проф. В.И.Шмальгаузен,
физфак МГУ, г.Москва
chesnok@ msuilc.phys.msu.su

Хочу учиться на ВМК!

Задачи, предлагавшиеся на вступительных экзаменах на факультет
вычислительной математики и кибернетики МГУ им. М.В.Ломоносова в 2003 г.

III. Электродинамика (окончание)

15 Горизонтально расположенный стержень равномерно вращается вокруг вертикальной оси, проходящей через один из его концов, с угловой скоростью . На другом конце стержня закреплён маленький шарик массой m, несущий заряд q. Вся система находится в однородном постоянном магнитном поле, индукция которого B направлена горизонтально. Найдите максимальное значение F_max силы F, с которой стержень действует на шарик в процессе движения, если известно, что минимальное значение силы F равно F_min. Силу тяжести не учитывать, размером шарика по сравнению с длиной стержня пренебречь.

Решение

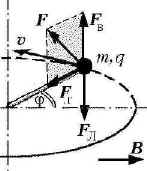
Силы, действующие на шарик в некоторой точке его траектории, изображены на рисунке. Здесь через F обозначена сила реакции стержня, а через F_Л – сила Лоренца, направленная перпендикулярно скорости стержня и вектору магнитной индукции, т.е. вертикально. Силу F удобно разложить на горизонтальную и вертикальную составляющие:

F = F_г + F_в.

Тогда Уравнения движения шарика в проекциях на горизонтальное и вертикальное направления имеют вид:

m²l = F_г; F_в = F_Л = qBcos,

где = l – скорость шарика, l – длина стержня, – угол между стержнем и вектором В. Отсюда

Минимальное значение этой силы достигается при = 90°, = 270°, а максимальное – при = 0, = 180°. Следовательно,

IV. ОПТИКА

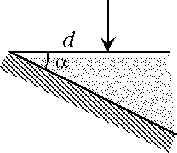
1 На верхнюю грань стеклянного клина с углом = 15° падает узкий пучок света перпендикулярно этой грани на расстоянии d = 2 см от ребра клина. Нижняя грань клина посеребрена. На каком расстоянии d₁ от ребра отражённый пучок выходит из клина?

Решение

Ход одного из лучей, образующих световой пучок, изображён на рисунке. Видно, что угол падения луча на посеребрённую грань клина равен , а отражённый от неё луч составляет с падающим лучом угол 2. Поэтому искомое расстояние

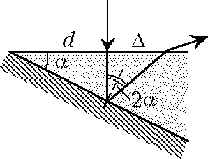
d₁ = d + ,

где 

Отсюда  

С использованием тригонометрических тождеств ответ легко преобразуется к виду:

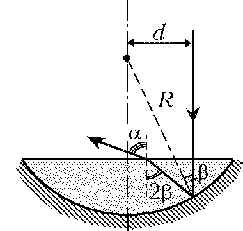
2 На плоскую поверхность плоско-выпуклой линзы, сферическая поверхность которой имеет радиус R и посеребрена, падает узкий пучок света параллельно главной оптической оси на расстоянии d от неё. Пучок выходит из линзы после однократного отражения от её сферической поверхности. Найдите, под каким углом к оси пучок выходит из линзы. Показатель преломления стекла, из которого изготовлена линза, равен n.

Решение

Ход одного из лучей, образующих световой пучок, изображён на рисунке, где через обозначен угол падения луча на посеребрённую поверхность линзы. Видно, что

Угол падения отражённого от посеребрённой поверхности луча на плоскую поверхность линзы составляет 2. По закону преломления,

Используя тождество получаем ответ:

3 На плоскую поверхность плоско-вогнутой линзы, вогнутая поверхность которой имеет радиус R и посеребрена, параллельно главной оптической оси на расстоянии d от неё падает узкий пучок света. Пучок выходит через плоскую поверхность линзы после отражения от сферической поверхности. Найдите, на каком расстоянии d₁ от оси выходит пучок из линзы, если толщина линзы на оси пренебрежимо мала.

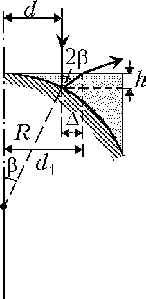
Решение

Ход одного из лучей изображён на рисунке, из которого видно, что где Учитывая, что  находим Используя далее тождество   получаем

4 Тонкая собирающая линза даёт на экране изображение предмета, увеличенное в n = 3 раза. Когда линзу переместили в сторону экрана на расстояние l = 32 см, на экране возникло изображение предмета, уменьшенное во столько же раз. Найдите фокусное расстояние линзы f.

Решение

Обозначим через a, b и a' и b' расстояния от предмета до линзы и от линзы до экрана в первом и во втором случаях соответственно. По условию задачи,

a' = a + l; b = b' – l.

Увеличение изображения в первом случае а во втором Дважды используя формулу тонкой линзы

получаем

5 Параллельный пучок света, падающий под углом ₁ = 60° на плоское зеркало, оказывает на него давление p₁ = 4 · 10^–6 Па. Какое давление p₂ будет оказывать на зеркало этот пучок, если угол падения пучка станет ₂ = 45°?

Решение

При отражении от зеркала импульс каждого фотона меняется на величину где p₀ – импульс падающего фотона, – угол падения. На зеркало площадью S за время t падает фотонов, где n – число фотонов в единице объёма, c – скорость света. Импульс силы, действующей на зеркало со стороны падающих фотонов за время t, равен

Следовательно, давление света, падающего на зеркало под углом ₁, равно

Аналогично для света, падающего на зеркало под углом ₂, Окончательно: