Абитуриенту

Продолжение. См. № 1/05

С.С.Чесноков, С.Ю.Никитин,
И.П.Николаев, Н.Б.Подымова,
М.С.Полякова, проф. В.И.Шмальгаузен,
физфак МГУ, г. Москва
chesnok@ msuilc.phys.msu.su

Хочу учиться на ВМК!

Задачи, предлагавшиеся на вступительных экзаменах
на факультет вычислительной математики и кибернетики МГУ им. М.В.Ломоносова в 2004 г.

I. МЕХАНИКА

1  Узнав о готовящемся нападении неприятеля, решётку ворот замка начали опускать с постоянной скоростью u = 0,2м/с. Мальчик, игравший на расстоянии l = 20 м от ворот, в тот же момент бросился бежать к воротам. Сначала он двигался равноускоренно, а затем, набрав максимальную скорость = 2,5м/с, равномерно. С каким минимальным ускорением а_min мог разгоняться мальчик, чтобы успеть пробежать под решёткой ворот в полный рост, если в начальный момент нижний край решетки находился на расстоянии Н = 3м от поверхности земли? Рост мальчика h = 1 м.

Решение

Пусть ускорение мальчика равно a. Тогда за время разгона он пробежит расстояние

Полное время движения мальчика до ворот равно

Из этого выражения видно, что, чем меньше ускорение мальчика на участке разгона, тем больше время t, через которое он достигнет ворот. С другой стороны, чтобы мальчик успел пробежать под решёткой ворот в полный рост, t не должно превышать времени движения решётки ворот от исходного положения до высоты, равной росту мальчика. Очевидно, что ускорение мальчика будет минимальным, если t = . Учитывая, что после несложных преобразований получаем ответ:

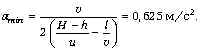
2   Лёгкий маленький шарик роняют без начальной скорости. Когда шарик пролетает по вертикали расстояние h, он ударяется о тяжёлую горизонтальную доску, движущуюся вертикально вверх с постоянной скоростью. После упругого удара о доску шарик подлетает вверх на высоту nh от точки соударения. С какой скоростью u двигалась доска? Сопротивлением воздуха пренебречь. Ускорение свободного падения равно .

Решение

Скорость шарика, свободно упавшего с высоты h, равна . Для того чтобы шарик после удара о доску поднялся на высоту nh, он должен при ударе приобрести скорость

направленную вверх. В системе отсчёта, связанной с доской, скорость шарика перед ударом Так как удар упругий, шарик отскочит вверх с такой же по модулю скоростью относительно доски: По закону сложения скоростей скорость шарика после удара в неподвижной системе отсчёта равна  

 Объединяя записанные выражения, получаем

3   Граната, брошенная под углом к горизонту, разорвалась в верхней точке траектории на два одинаковых осколка. Один из осколков упал на землю через время t₁ после разрыва. Через какое время t₂ после разрыва окажется на земле второй осколок, упавший позднее первого, если разрыв произошёл на высоте h над землёй? Сопротивлением воздуха пренебречь. Ускорение свободного падения равно .

Решение

Поскольку разрыв гранаты происходит в верхней точке траектории, непосредственно перед разрывом вертикальная составляющая импульса системы равна нулю. Считая разрыв кратковременным и пренебрегая импульсом силы тяжести за время разрыва, можно применить закон сохранения импульса. С учётом того, что массы осколков одинаковы, из этого закона следует, что вертикальные составляющие скоростей осколков сразу после разрыва гранаты равны по величине и противоположны, причём, судя по условию задачи, скорость первого осколка направлена вниз, а скорость второго – вверх. Выбирая начало отсчёта в точке разрыва гранаты и направляя координатную ось Y вниз, имеем:

 где ₀ – модуль вертикальной скорости осколков. Кинематическое уравнение движения по вертикали, записанное для первого осколка, даёт соотношение

Отсюда Аналогично для второго осколка имеем:

Подставляя сюда найденное ₀ , получаем уравнение

Условию задачи удовлетворяет положительный корень. Поэтому

4   При поливе садового участка наконечник водопроводного шланга расположили на высоте h = 0,8 м над землёй, направив струю воды вверх под углом = 30° к горизонту. Найдите массу m воды, содержащейся в отрезке струи от наконечника шланга до земли. Скорость воды, бьющей из шланга, ₀ = 6 м/с, внутреннее сечение наконечника шланга S = 3 см², плотность воды = 103 кг/м³. Ускорение свободного падения = 10 м/с².

Решение

Расход воды, определяемый как масса воды, вытекающей из шланга в единицу времени, равен Поэтому масса воды, находящейся в данный момент в воздухе, может быть найдена из выражения

где – время движения частицы воды в струе от вылета из шланга до падения на землю. Пусть начало координат находится на земле, а ось Y направлена вверх. Из кинематического уравнения для движения частицы воды по вертикали следует:

 Положительный корень этого уравнения

 Подставляя найденное   в выражение для массы воды, получаем окончательно

5   На гладком столе лежит доска, к которой вплотную прижат брусок. Коэффициент трения между бруском и доской
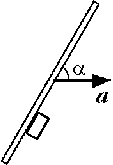
= 0,1. Доску начинают поступательно перемещать по столу с некоторым постоянным ускорением. При каком минимальном значении угла a между плоскостью доски и вектором ускорения брусок не будет скользить по доске?

Решение

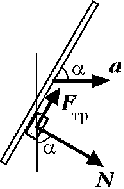
Силы, действующие на брусок в горизонтальной плоскости, показаны на рисунке, где через F_тр обозначена сила трения, а через N – нормальная составляющая силы реакции доски. Брусок не скользит по доске, если проекция суммы этих сил на направление, перпендикулярное ускорению доски, равна нулю:

Минимальное значение угла достигается, когда сила трения покоя принимает максимальное значение F_тр = N. Объединяя записанные выражения, получаем