Продолжение. См. № 1, 3/05
6 Обруч
диаметром D располагается в вертикальной
плоскости. В точке A, лежащей на верхнем
конце вертикального диаметра обруча, на шарнире
закреплен жёлоб, угол наклона которого можно
менять. По жёлобу из точки A пускают
скользить без начальной скорости небольшой
брусок. Найдите зависимость времени ![]() , через которое
брусок достигнет точки пересечения жёлоба и
обруча, от угла
, через которое
брусок достигнет точки пересечения жёлоба и
обруча, от угла ![]() , который жёлоб образует с вертикалью.
Коэффициент трения бруска о жёлоб
, который жёлоб образует с вертикалью.
Коэффициент трения бруска о жёлоб ![]() , ускорение свободного
падения
, ускорение свободного
падения ![]() .
.
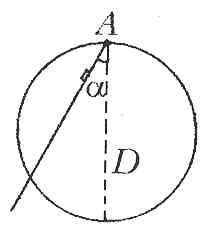
Решение
Уравнение движения бруска по жёлобу,
составляющему угол ![]() с вертикалью, имеет вид:
с вертикалью, имеет вид:
![]()
откуда ускорение бруска ![]()
Из кинематического соотношения ![]() где L
= Dcos
где L
= Dcos![]() – путь, пройденный бруском до точки пересечения
жёлоба с обручем, получаем ответ:
– путь, пройденный бруском до точки пересечения
жёлоба с обручем, получаем ответ:
![]()
В диапазоне ![]() время движения бруска
увеличивается с ростом
время движения бруска
увеличивается с ростом ![]() . При
. При ![]() брусок, предоставленный
самому себе, двигаться не будет.
брусок, предоставленный
самому себе, двигаться не будет.
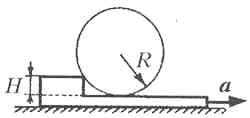
7 На
горизонтальной доске, имеющей прямоугольный
уступ высотой H = 10 см, располагается
вплотную к уступу однородный цилиндр радиусом R
= 25 см. Доску начинают двигать с некоторым
ускорением a, направленным вправо.
Каково максимально возможное значение ускорения
amax, при котором цилиндр не будет подниматься на
уступ? Все поверхности гладкие. Ускорение
свободного падения ![]() = 9,8 м/с2.
= 9,8 м/с2.
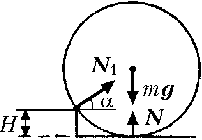
Решение
Пусть ускорение доски таково, что
цилиндр не перекатывается через уступ, а
движется поступательно вместе с доской. Силы,
действующие на цилиндр в этом случае, изображены
на рисунке, где через m![]() обозначена сила
тяжести (m – масса цилиндра), через N
– сила реакции горизонтальной части доски, а
через N1 – сила реакции
уступа. Поскольку трение, по условию задачи,
пренебрежимо мало, вектор силы N1
направлен перпендикулярно касательной к
поверхности цилиндра, т.е. по радиусу к его оси. В
проекциях на горизонтальное и вертикальное
направления уравнения движения цилиндра имеют
вид:
обозначена сила
тяжести (m – масса цилиндра), через N
– сила реакции горизонтальной части доски, а
через N1 – сила реакции
уступа. Поскольку трение, по условию задачи,
пренебрежимо мало, вектор силы N1
направлен перпендикулярно касательной к
поверхности цилиндра, т.е. по радиусу к его оси. В
проекциях на горизонтальное и вертикальное
направления уравнения движения цилиндра имеют
вид:
![]()
![]()
Если увеличивать ускорение доски, то модуль силы N1 будет возрастать, а модуль силы N – уменьшаться. Наконец, при максимально возможном ускорении доски, при котором цилиндр ещё не будет подниматься на уступ, N обратится в нуль. Из уравнений движения для этого случая находим
![]()
где ![]() – угол между горизонталью и вектором N1.
Выражая ctg
– угол между горизонталью и вектором N1.
Выражая ctg![]() через заданные в условии радиус
цилиндра и высоту уступа, получаем
через заданные в условии радиус
цилиндра и высоту уступа, получаем
![]()
8 На горизонтальной
шероховатой поверхности находится маленький
брусок. Если на брусок подействовать в течение
очень короткого промежутка времени
горизонтальной силой, равной по модулю F и
значительно превышающей силу трения скольжения,
то после этого брусок пройдёт до остановки путь s0.
Какой путь s пройдёт до остановки этот
брусок, если в течение того же промежутка времени
на него одновременно подействовать тремя
горизонтальными силами с тем же модулем F,
две из которых направлены под углами ![]() = 60° к третьей?
= 60° к третьей?
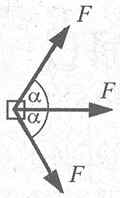
Решение
Обозначим через t время действия
силы F. По закону изменения
импульса, имеем ![]() где m – масса бруска,
где m – масса бруска, ![]() 0
– скорость, которую он приобретает в результате
действия силы F (импульсом силы
трения за время
0
– скорость, которую он приобретает в результате
действия силы F (импульсом силы
трения за время ![]() , по условию задачи, можно пренебречь). По
закону изменения механической энергии:
, по условию задачи, можно пренебречь). По
закону изменения механической энергии:
![]()
где ![]() – коэффициент трения. Величина
равнодействующей трёх сил, действующих на брусок
одновременно и направленных, как показано на
рисунке, равна
– коэффициент трения. Величина
равнодействующей трёх сил, действующих на брусок
одновременно и направленных, как показано на
рисунке, равна
![]()
Законы изменения импульса и энергии в этом случае дают:
![]()
![]()
Объединяя записанные выражения, находим
![]()
9
Однородная тяжёлая цепочка, состоящая из мелких
звеньев, подвешена за концы, как показано на
рисунке. Точка C – самая нижняя точка
цепочки. Определите массу цепочки m, если
известно, что величины силы натяжения цепочки в
точках A, B, C равны соответственно TA,
TB, TC.
Ускорение свободного падения ![]() .
.

Решение
На каждое звено цепочки действуют
силы, изображённые на рисунке, где через m![]() обозначена сила тяжести, а через T и
T' – силы, приложенные к этому звену
со стороны соседних звеньев. Поскольку цепочка
висит неподвижно, каждое звено находится в
состоянии равновесия и сумма сил, действующих на
него, равна нулю. Полагая, что масса каждого звена
мала, можно считать, что силы T и T'
равны по величине и направлены в противоположные
стороны по касательной к цепочке. Модуль каждой
из этих сил и представляет собой натяжение
цепочки в данном сечении.
обозначена сила тяжести, а через T и
T' – силы, приложенные к этому звену
со стороны соседних звеньев. Поскольку цепочка
висит неподвижно, каждое звено находится в
состоянии равновесия и сумма сил, действующих на
него, равна нулю. Полагая, что масса каждого звена
мала, можно считать, что силы T и T'
равны по величине и направлены в противоположные
стороны по касательной к цепочке. Модуль каждой
из этих сил и представляет собой натяжение
цепочки в данном сечении.
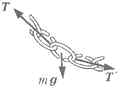
На рисунке изображены силы натяжения, действующие на отрезки цепочки AC и CB. Из соображений симметрии ясно, что силы, возникающие в точке C, а именно TC и T'C, направлены горизонтально. При этом T 'C = TC. Условия равновесия цепочки имеют вид:
![]()
![]()
![]()
Исключая из этих равенств углы ![]() и
и ![]() , получаем
, получаем
![]()