Продолжение. См. № 1, 3, 5, 7 /05
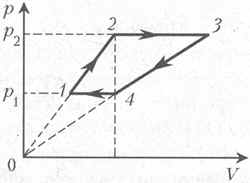
2 Над идеальным одноатомным газом постоянной массы проводят процесс, диаграмма которого изображена на рисунке. Найдите работу A, совершаемую газом в этом процессе, если на участке 2–3 газ получает количество теплоты Q23=200 Дж. Объём газа в точках 2 и 4 один и тот же, давление газа в точке 2 в два раза больше давления газа в точке 1.
Решение
Работа газа численно равна площади фигуры, которую ограничивает график процесса на плоскости переменных p и V (в данной задаче – площади трапеции):
Полученное газом количество теплоты
Из уравнений процессов 1–2 и 4–3 следует, что
Отсюда V2=2V1; V3=4V1. Используя эти соотношения, преобразуем выражения для работы газа и полученного им количества теплоты к виду:
из которого легко получить 
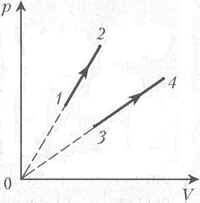
3 На рисунке изображены p, V – диаграммы двух процессов, проводимых над одним и тем же идеальным одноатомным газом. Масса газа, участвующего в процессе 1–2, в k=2 раза больше, чем масса газа, с которым проводится процесс 3–4. Температура в точке 1 равна температуре в точке 3, а температура в точке 2 равна температуре в точке 4. Найдите отношение n количеств теплоты, получаемых газом в процессах 1–2 и 3–4.
Решение
Для расчёта количества теплоты, полученного газом, воспользуемся первым законом термодинамики. Рассмотрим сначала процесс 1–2. Изменение внутренней энергии газа и работа, совершённая газом в этом процессе, соответственно равны:
Здесь n1 – число молей газа, участвующего в процессе 1–2; pi, Vi, Ti – давление, объём и температура газа в точке i (i =1, 2). Поскольку точки 1 и 2 лежат на прямой, проходящей через начало координат, справедливо равенство
Используя это равенство, а также уравнения состояния газа в точках 1 и 2:
выражение для работы газа легко преобразовать к виду:
Из первого закона термодинамики следует, что количество теплоты, полученное газом в процессе 1–2, равно
Рассуждая аналогично, находим количество теплоты, полученное газом в процессе 3–4:
где 
– количество газа, участвующего в этом
процессе. Поскольку, по условию задачи, T3=T1,
T4=T2, выражение для Q34
преобразуется к виду:
Тогда 
4 В
теплоизолированном цилиндрическом сосуде под
поршнем массой m находится идеальный одноатомный
газ. Расстояние между поршнем и дном сосуда равно
x. На какое расстояние 
опустится поршень,
если сверху положить на него груз массой 
?
Считать, что 
начальное и конечное положения поршня
являются положениями равновесия, трение поршня о
стенки сосуда пренебрежимо мало. Атмосферное
давление не учитывать.
Решение
Поскольку газ теплоизолирован, из
первого закона термодинамики следует, что 
где 
–
изменение внутренней энергии газа, 
– работа,
совершённая над газом. Для газа справедливо
также уравнение состояния (уравнение
Клапейрона–Менделеева):
Пусть p0, V0 и T0
– параметры начального состояния, а 
и 
– параметры
конечного состояния газа. Так как изменения
параметров состояния газа также малы:
С точностью до малых первого порядка из уравнения Клапейрона–Менделеева получаем
Кроме того, с той же точностью имеем
Подставляя найденные выражения в
равенство получаем, что
Поскольку 
и 
получаем 
5 Трубка поперечного сечения S, заполненная водяным паром под давлением p, запаяна с двух концов и расположена горизонтально. При этом находящийся в трубке поршень делит трубку на две равные части. Трубку ставят вертикально, в результате чего поршень смещается и объём под ним уменьшается в четыре раза. Найдите массу поршня m, если давление насыщенного водяного пара равно 2p. Трением и толщиной поршня пренебречь, температуру пара считать постоянной. Ускорение свободного падения g.
Решение
При перемещении поршня давление пара в нижней части трубки увеличится до величины 2p, после чего будет оставаться постоянным. При этом часть пара сконденсируется. Пар над поршнем можно считать идеальным газом. Его давление, согласно закону Бойля–Мариотта, равно
Из условия равновесия поршня имеем: p1S + mg = 2pS.
Объединяя записанные выражения, получаем: 