Продолжение. См. № 4, 6, 8, 10, 12, 16, 18/05
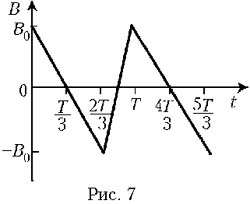
7 Кольцо радиусом а из тонкой медной проволоки, имеющее сопротивление R, удерживают в однородном магнитном поле, линии индукции которого перпендикулярны плоскости кольца. Проекция B вектора индукции на ось кольца изменяется с периодом Т по закону, изображённому на рис. 7. Пренебрегая индуктивностью кольца, найдите среднюю тепловую мощность за период, выделяющуюся в кольце.
Решение
Согласно приведённому графику, в
течение промежутков времени 
и 
проекция вектора индукции однородного
внешнего магнитного поля на ось кольца
равномерно изменяется на величину 2B0. По условию
задачи, кольцо изготовлено из тонкой проволоки и
его индуктивностью следует пренебречь. Поэтому
можно не учитывать магнитный поток, сцепленный с
материалом кольца, и пренебречь потоком
магнитного поля, порождаемого током в кольце.
Считая, как обычно, что кольцо и источник
магнитного поля покоятся относительно
инерциального наблюдателя, на основании закона
электромагнитной индукции (правила потока
Фарадея–Максвелла) можно утверждать, что в
течение времени 
1
= 2T/3 в кольце действуют сторонние электрические
силы, величина ЭДС которых равна
а в оставшуюся часть периода (2 = T/3)
величина ЭДС индукции равна
Поскольку индуктивностью кольца следует пренебречь, то, согласно закону Ома, в течение первой и второй частей периода сила тока в кольце равна:
а потому, согласно закону Джоуля–Ленца, в кольце за период Т должно выделяться количество теплоты
Вспоминая, что средняя за период тепловая мощность равна отношению количества теплоты, выделившегося за период, к длительности периода, получаем, что искомая тепловая мощность равна
1 Точечный источник света расположен на главной оптической оси на расстоянии a = 30 см от тонкой собирающей линзы, оптическая сила которой равна D = 5 дптр. Диаметр линзы d = 1 см. На какое расстояние х сместится изображение источника, если между ним и линзой поместить, перпендикулярно главной оптической оси линзы, стеклянную пластинку толщиной h = 15 см и показателем преломления n = 1,57?
Решение
Будем решать задачу, полагая, что рассматриваемая оптическая система находится в однородной изотропной среде, а n – относительный показатель преломления стекла по отношению к этой среде. По условию задачи, отношение диаметра d линзы к расстоянию а, на котором находится от неё точечный источник S, существенно меньше единицы. Поэтому можно считать, что все лучи от этого источника, проходящие через линзу, образуют с её главной оптической осью углы значительно меньше одного радиана. Следовательно, выполняется так называемое параксиальное приближение, а потому все прошедшие сквозь линзу лучи должны пересекаться в одной точке, создавая действительное точечное изображение источника, находящееся, согласно формуле тонкой линзы, на расстоянии b = a/(aD – 1) от её главной плоскости. Утверждая это, мы учли, что источник находится перед линзой на расстоянии a = 30 см, большем её фокусного расстояния F = D–1 = 20 см.
После установки пластинки все
падающие на линзу лучи, за исключением луча,
идущего вдоль главной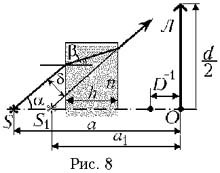 
оптической оси
линзы, будут испытывать преломление в пластинке,
т.к. плоские грани пластинки, по условию задачи,
перпендикулярны главной оптической оси линзы. На
рис. 8 показан ход одного из лучей, образующих с
главной оптической осью линзы Л угол 
. После преломления на
передней грани пластинки этот луч будет
распространяться в пластинке под углом 
к перпендикуляру,
восстановленному в точке падения к поверхности
пластинки. Учитывая, что пластинка является
плоскопараллельной и по обе стороны от неё
находится одна и та же среда, на основании закона
преломления можно утверждать, что после
прохождения пластинки направление
распространения луча не изменится, но он
сместится на расстояние 
. Обратившись к рис. 8, можно показать,
что 
а точка S1
пересечения продолжения выходящего из пластинки
луча с главной оптической осью линзы сместится к
линзе относительно источника S на расстояние
При малых углах и
можно считать, что продолжения всех лучей,
выходящих из пластинки под малыми углами к её
нормали и попадающих на линзу, пересекаются в
одной точке S1, находящейся перед линзой на
расстоянии a1 = a – SS1 = a – (1 – n–1)h. Изображение
этой точки, согласно формуле тонкой линзы, должно
находиться от главной плоскости линзы на
расстоянии b1 = a1/(a1D – 1). Таким образом, при
выполнении сделанных выше предположений
изображение источника удалится от главной
плоскости линзы на расстояние
2 На
горизонтальную поверхность стекла налит тонкий
слой жидкости показателем преломления n. На
жидкость сверху под углом к вертикали падает параллельный пучок
света длиной волны 
. Жидкость медленно испаряется. В
некоторый момент интенсивность отражённого
света становится максимальной, а затем убывает и
вновь становится максимальной через промежуток
времени .
Найдите скорость 
,
с которой уменьшается толщина слоя жидкости
из-за испарения.
Решение
Из условия задачи следует, что участок
верхней границы жидкости, освещаемый светом,
нужно считать горизонтальным, а изменение
интенсивности света обусловлено интерференцией
световых пучков, отражённых от границ жидкости.
На рис. 9 показан ход двух лучей падающего пучка.
Часть первого луча, испытав преломление на
верхней границе жидкости в точке А, под углом падает на границу
жидкость–стекло в точке В и после частичного
отражения от стекла, испытав преломление на
верхней границе, выходит из жидкости в точке С.
Второй луч, падающий на верхнюю границу жидкости
в точке С, испытывает частичное отражение от этой
границы. Основываясь на законах отражения и
преломления света, можно доказать, что выходящая
из жидкости часть первого луча и отражённая от
верхней границы жидкости часть второго луча
будут распространяться в одном и том же
направлении (под углом к вертикали) и могут интерферировать.
По условию задачи, налитый слой
жидкости тонкий, а потому следует считать, что
разность фаз налагающихся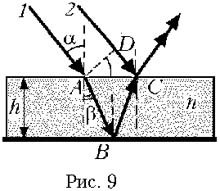 
лучей не
зависит от времени, т.е. эти лучи следует считать
когерентными. Поэтому в те моменты времени, когда
наблюдается максимум интенсивности отражённого
света, оптическая разность хода налагающихся
лучей должна быть кратна целому числу длин волн падающего на
поверхность жидкости света. При вычислении
разности хода учтём, что при отражении света от
оптически более плотной среды происходит
«потеря половины длины волны», а потому к
разности хода налагающихся лучей следует
добавить половину длины волны. Если же отражение
происходит от оптически менее плотной среды, то
указанное явление отсутствует. Следовательно,
если показатель n1 преломления стекла больше n, то
разность хода этих лучей (рис. 9) равна
т.к. 
При n1 < n разность хода
При максимальной интенсивности 
где k – порядок
интерференционного максимума. Поскольку за
время толщина
слоя уменьшается на 
а порядок интерференции на единицу, то
Таким образом, средняя скорость уменьшения толщины слоя жидкости вне зависимости от соотношения между показателями преломления жидкости и стекла равна
