В 2004 г. на физическом факультете Московского государственного университета им. М.В.Ломоносова проводились два тура физико-математической олимпиады (в марте и мае) и один вступительный экзамен (в начале июля). Олимпиадные задания и экзаменационные билеты по физике содержали два теоретических вопроса, формулировки которых были взяты из программы по физике, опубликованной в справочнике для поступающих в МГУ, и две задачи. Ниже приводятся условия предлагавшихся задач и их решения. В решениях особое внимание уделено обоснованию возможности применения того или иного закона и указаны предположения, в том числе и так называемые стандартные, которые необходимо было сделать в ходе решения.
По всем вопросам приёма обращайтесь по телефону 939-1241 в совет по новому приёму и работе со школьниками физического факультета МГУ.
1 На противоположных берегах прямолинейного
участка реки на расстоянии L друг от друга
находятся пристани А и В. Прямая АВ
образует угол ![]() с берегом. От пристаней одновременно с
одинаковыми по величине скоростями
с берегом. От пристаней одновременно с
одинаковыми по величине скоростями ![]() отошли два катера.
Катера шли вдоль прямой АВ и встретились
через время
отошли два катера.
Катера шли вдоль прямой АВ и встретились
через время ![]() после отправления. Найдите величину
скорости катеров
после отправления. Найдите величину
скорости катеров ![]() . Скорость течения реки считайте
постоянной и равной u.
. Скорость течения реки считайте
постоянной и равной u.
Решение
В условии задачи не сказано, какая из
двух пристаней расположена ниже по течению.
Поэтому в данной задаче необходимо рассмотреть
два случая. В первом случае будем считать, что
пристань В находится ниже по течению, а во втором
– выше. Будем искать решение, полагая, как это
обычно и делается в подобных задачах, что катера
полностью «увлекаются» водой. При выполнении
этого предположения на основании принципа
независимого сложения движений можно
утверждать, что скорость ![]() i движения катера
относительно берега должна быть равна векторной
сумме скорости течения u и скорости катера
относительно воды
i движения катера
относительно берега должна быть равна векторной
сумме скорости течения u и скорости катера
относительно воды ![]() . Поскольку, по условию задачи,
катера должны двигаться вдоль прямой,
соединяющей пристани, то направления их
скоростей относительно берега должны совпадать
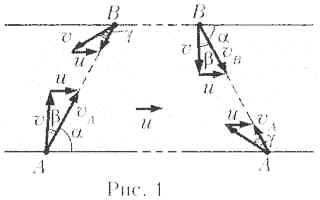
с прямой АВ. С учётом сказанного на рис. 1
изображены оба удовлетворяющие условию задачи
случая, причём около векторов скоростей катеров
указаны их модули.
. Поскольку, по условию задачи,
катера должны двигаться вдоль прямой,
соединяющей пристани, то направления их
скоростей относительно берега должны совпадать
с прямой АВ. С учётом сказанного на рис. 1
изображены оба удовлетворяющие условию задачи
случая, причём около векторов скоростей катеров
указаны их модули.
С учётом показанных на этом рисунке обозначений углов между величинами скоростей катеров относительно берега и воды справедливы соотношения
![]() (1)
(1)
поэтому ![]() Следовательно, величины
скоростей катеров относительно берега в первом
случае равны
Следовательно, величины
скоростей катеров относительно берега в первом
случае равны
![]()
![]() (2)
(2)
а во втором
![]()
![]() (3)
(3)
Поскольку катера одновременно
отплывают от пристаней и до встречи должны
переместиться друг относительно друга на
расстояние L за время ![]() , а величина скорости их сближения
равна
, а величина скорости их сближения
равна
![]()
то ![]() т.к., согласно соотношению (1),
т.к., согласно соотношению (1), ![]() Решая
предпоследнее уравнение, находим искомую
величину скорости движения катеров относительно
воды:
Решая
предпоследнее уравнение, находим искомую
величину скорости движения катеров относительно
воды:
![]()
2 Маленькая шайба соскальзывает без начальной скорости с высоты Н по гладкой наклонной плоскости и упруго ударяется о горизонтальную площадку. В момент удара с этой площадки вертикально вверх бросают камешек с такой скоростью, чтобы он поднялся на высоту, которая в n раз меньше Н. На каком расстоянии L от линии пересечения площадки с наклонной плоскостью находилась точка броска, если шайба ударилась о камешек до того момента, когда они вторично ударились о площадку? Влиянием воздуха на движение тел пренебречь.
Решение
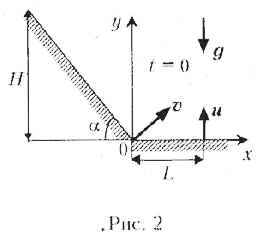
При решении задачи будем использовать
лабораторную систему отсчёта, расположенную
относительно наклонной плоскости и
горизонтальной площадки так, как показано на рис.
2. Как обычно, будем считать эту лабораторную
систему отсчёта инерциальной. Поскольку шайба
соскальзывает без начальной скорости по гладкой
наклонной плоскости, а влиянием воздуха на
движение шайбы и её размерами, по условию задачи,
следует пренебречь, то, согласно закону
сохранения механической энергии в системе
шайба–Земля, величина скорости шайбы перед
самым ударом о горизонтальную площадку должна
быть равна ![]() где
где ![]() –
величина ускорения свободного падения. При
выводе этого соотношения было учтено, что масса
Земли во много раз превышает массу шайбы.
–
величина ускорения свободного падения. При
выводе этого соотношения было учтено, что масса
Земли во много раз превышает массу шайбы.
По условию задачи, удар шайбы о
горизонтальную площадку является упругим.
Поэтому на основании законов сохранения
импульса и механической энергии в системе
шайба–Земля и с учётом малых размеров шайбы
можно утверждать, что после удара горизонтальная
составляющая скорости шайбы останется
неизменной, а вертикальная, сохранив свою
величину, изменит направление на
противоположное. Таким образом, в момент броска
камешка составляющие скорости шайбы должны быть
равны ![]()
![]() где
где ![]() – угол наклона плоскости к горизонту
(см. рис. 2). Следовательно, если начать
отсчитывать время t от момента окончания удара
шайбы о площадку, то до момента соударения шайбы
с камешком, т.е. при
– угол наклона плоскости к горизонту
(см. рис. 2). Следовательно, если начать
отсчитывать время t от момента окончания удара
шайбы о площадку, то до момента соударения шайбы
с камешком, т.е. при ![]() закон движения шайбы в
выбранной системе отсчёта можно представить в
виде:
закон движения шайбы в
выбранной системе отсчёта можно представить в
виде: ![]()
![]()
По условию задачи, камешек был брошен
вертикально вверх с такой скоростью, что мог бы
подняться на высоту H/n, если бы о него не
ударилась шайба. Поэтому, пренебрегая массой
камешка по сравнению с массой Земли и учитывая,
что камешек до момента удара о него шайбы, по
условию задачи, совершает свободное падение,
согласно закону сохранения механической энергии
в системе камешек–Земля, начальная скорость
камешка должна быть равна ![]() Следовательно, закон
движения камешка при
Следовательно, закон
движения камешка при ![]() можно представить в виде:
можно представить в виде:
![]()
![]()
Учитывая, что в момент удара t = ![]() соответствующие координаты шайбы и камешка
должны быть равны, получим:
соответствующие координаты шайбы и камешка
должны быть равны, получим:
![]()
![]()
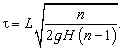
По условию задачи, соударение шайбы с камешком должно было произойти до того момента, когда они вторично ударятся о площадку. Следовательно, момент соударения шайбы с камешком должен удовлетворять неравенству
![]()
а потому
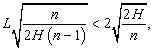
и искомое расстояние от линии пересечения площадки с наклонной плоскостью до точки, из которой был брошен камешек,
![]()