Продолжение. См. № 4, 6, 8, 10, 12/05
1 Два маленьких
шарика, один из которых первоначально покоился, а
второй имел некоторую скорость 
, находясь от первого шарика на
очень большом расстоянии, сблизились до
расстояния L. Зная, что направление скорости
второго шарика оставалось неизменным, найти
величину скорости v. Влиянием на шарики всех
других тел и потерями энергии шариков на
излучение пренебречь. Масса первого шарика равна
m, второго – М. Заряд каждого шарика равен q.
Решение
По условию задачи, на шарики не
действуют другие тела. Поэтому можно считать, что
первоначальное состояние системы, состоящей из
шариков, задано относительно инерциального
наблюдателя и эта система является
изолированной. Поскольку направление скорости
второго шарика остаётся неизменным, нужно
считать, что оба шарика при сближении движутся
вдоль одной прямой, и в момент наибольшего
сближения относительная скорость шариков
обращается в нуль, т.е. скорости шариков в этот
момент относительно указанного наблюдателя
становятся равными: 
Поскольку шарики образуют изолированную систему, в которой не действуют диссипативные силы, то в любой момент времени, в том числе и в момент наибольшего сближения шариков, должны выполняться закон сохранения импульса и закон сохранения энергии:
где 
–
электрическая постоянная. При записи закона
сохранения энергии было учтено, что шарики
движутся поступательно, а потерями механической
энергии, обусловленными излучением движущихся с
ускорением заряженных тел, по условию задачи,
следует пренебречь.
Решая совместно приведённые
уравнения, находим искомую величину скорости: 
2 На тонкий гладкий горизонтальный диэлектрический стержень надеты две маленькие бусинки зарядами +q и –q, скреплённые между собой диэлектрической пружиной жёсткостью k. Вся система находится в однородном электрическом поле, силовые линии которого параллельны стержню. При этом пружина не деформирована. Если изменить направление поля на противоположное, оставив неизменной величину его напряжённости Е, то длина пружины при равновесии уменьшится в n = 2 раза. Пренебрегая поляризацией диэлектриков, найти величину Е.
Решение
Будем считать, что стержень с шариками и источник внешнего электрического поля покоятся относительно некоторой инерциальной системы отсчёта. Тогда, пренебрегая в соответствии с условием задачи силами трения между шариками и стержнем и поляризацией пружины и стержня, можно утверждать, что силы, действовавшие на шарики со стороны электрического поля при первоначальной ориентации вектора напряжённости этого поля, уравновешивали силы взаимного притяжения шариков, т.е. имело место соотношение
где l0 – длина недеформированной
пружины, – электрическая постоянная.
После изменения направления вектора напряжённости внешнего поля в конечном равновесном состоянии длина пружины, по условию задачи, становится в n раз меньше первоначальной. Следовательно, в соответствии с законами Кулона и Гука должно выполняться соотношение
Подставляя в это выражение значение qE
из предыдущего уравнения, находим, что длина
пружины в недеформированном состоянии должна
удовлетворять соотношению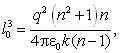 
а искомая величина
напряжённости поля равна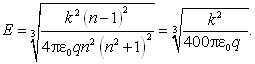 
3 На расстоянии 2R от центра закреплённого проводящего шара радиусом R удерживают положительный точечный заряд 2Q. Заряд шара равен Q. Какую скорость v может приобрести электрон, начинающий своё движение из бесконечно удалённой точки, к моменту попадания на шар?
Решение
При решении задачи будем предполагать, что шар покоится относительно некоторой инерциальной системы отсчёта, электрон движется в вакууме и можно пренебречь потерями энергии электрона на излучение, т.е. будем считать, что ускорение электрона достаточно мало. При приближении электрона к шару в силу явления электростатической индукции должно происходить перераспределение зарядов шара. Будем считать, что материал шара обладает достаточно большой проводимостью, а потому можно пренебречь потерями энергии, вызванными выделением джоулева тепла при протекании токов проводимости, и считать, что все точки проводящего шара имеют одинаковый потенциал, а потому весь его избыточный заряд, как и в электростатике, распределён только по поверхности шара.
Пусть величина заряда, находящегося на
достаточно малом i-м кусочке поверхности шара,
равна 
qi. По
условию задачи, шар изолирован, a его заряд равен
Q. Поэтому, согласно закону сохранения заряда и
сделанным выше предположениям, в любой момент
времени 
по всем кусочкам поверхности шара равна
Q.
Будем, как обычно, считать, что потенциал электростатического поля, создаваемого покоящимся точечным зарядом q в бесконечно удалённой от него точке, равен нулю. Тогда потенциал электростатического поля на расстоянии r от точечного заряда, как известно, будет равен
где – электрическая
постоянная. Согласно принципу суперпозиции
потенциал, создаваемый системой точечных
зарядов в данной точке, равен сумме потенциалов,
создаваемых каждым из этих зарядов порознь в
этой точке. Следовательно, потенциал центра шара
относительно бесконечно удалённой от него точки,
обусловленный избыточным зарядом шара и
точечным зарядом 2Q, находящимся от центра шара на
расстоянии 2R, равен
Согласно сказанному выше, таким же
должен быть потенциал и любой точки поверхности
шара, причём из полученного выражения следует,
что этот потенциал не зависит от положения
электрона. Поэтому при выполнении сделанных выше
предположений работа сил электростатического
поля, порождаемого зарядами шара и зарядом 2Q, над
перемещающимся в этом поле электроном не зависит
от вида траектории электрона, а определяется
лишь его начальным и конечным положениями.
Поскольку заряд электрона отрицателен,
указанное поле в ходе движения электрона к шару
совершит над электроном положительную работу 
где 
– модуль заряда
электрона. Отсюда, согласно закону изменения
кинетической энергии, следует, что искомая
величина скорости электрона массой m при его
попадании на поверхность шара с учётом потерь
энергии электрона на излучение и джоулево тепло
в шаре должна удовлетворять неравенству
4 В схеме, показанной на рис. 1, через резистор R1 = 15 Ом течёт ток I = 10 А, величина которого не зависит от положения движка реостата R. Найти величины ЭДС батарей в этой схеме, если внутреннее сопротивление первой батареи r1 = 5 Ом.
Решение
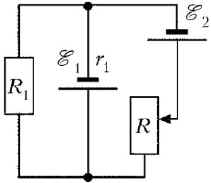
Рис. 1
При решении задачи будем, как обычно,
пренебрегать сопротивлением проводов и
контактов между элементами схемы. Поскольку
резистор R1, первая батарея и вторая батарея
вместе с реостатом R соединены параллельно,
падения напряжения на резисторе R1 на
первой батарее и на второй батарее с реостатом R
должны быть одинаковыми. Пусть сумма внутреннего
сопротивления второй батареи и включённой в
схему части реостата R равна r2. Тогда,
согласно сказанному и закону Ома, должны
выполняться соотношения: 
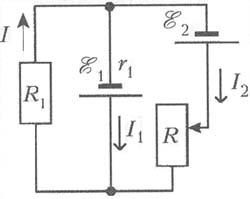
Рис. 2
При написании этих соотношений
предполагалось, что направления токов в ветвях
схемы соответствуют стрелкам, показанным на рис.
2. В силу закона сохранения заряда и постоянства
токов в ветвях схемы при указанных направлениях
токов их величины должны удовлетворять
соотношению I = I1 + I2, а потому сила
тока через резистор R1 должна удовлетворять
уравнению 
Это уравнение будет тождеством при
любых r2, если 
= IR1 (т.е. I2 = 0) и 
= I(R1 + r1). Таким
образом, искомые величины ЭДС равны:
5 По двум
параллельным шинам, закреплённым под углом 
= 45°
к горизонту, может скользить, оставаясь
перпендикулярной им, перемычка. Шины соединены
между собой неподвижным проводником.
Сопротивление перемычки много больше
сопротивления шин и проводника. Вся система
находится в однородном магнитном поле, индукция
которого B перпендикулярна плоскости шин. Если
направление магнитного поля сделать
вертикальным, не изменяя величины B, то
установившаяся скорость перемычки будет
отличаться в k = 0,8 раза от ранее наблюдавшейся.
Пренебрегая индуктивностью проводящего контура,
найти коэффициент трения 
перемычки о шины.
Решение
При решении задачи будем считать, что
шины и соединяющий их проводник неподвижны
вместе с источником магнитного поля
относительно лабораторной системы отсчёта и эта
система является инерциальной. При движении
перемычки будет изменяться поток магнитного
поля, сцепленный с проводящим контуром,
образованным перемычкой, шинами и соединяющим их
проводником. Поэтому в этом контуре должен
возникнуть индукционный ток, направление
которого, согласно правилу Ленца, должно быть
таким, чтобы движение перемычки тормозилось.
Тормозить движение перемычки будут и силы
трения, действующие на перемычку со стороны шин.
Следовательно, перемычка в установившемся
режиме может скользить по шинам только вниз. С
учётом сказанного, на рис. 3 показаны силы,
действующие на скользящую вниз по шинам
перемычку, когда вектор индукции В внешнего
магнитного поля направлен перпендикулярно
шинам. Здесь mg – сила тяжести, m – масса
перемычки, g – ускорение свободного падения. Сила
реакции шин показана на рисунке в виде двух
составляющих: нормальной N и тангенциальной Fтр,
называемой обычно силой сухого трения
скольжения, величина которой, согласно закону
Кулона–Амонтона, равна N. Наконец, FA – сила Ампера.
Согласно закону Ампера, эта сила направлена
перпендикулярно вектору В индукции магнитного
поля и перемычке, т.е. параллельно шинам, причём
из двух возможных направлений выбрано то,
которое, как было отмечено выше, согласуется с
правилом Ленца. Из сказанного и второго закона
Ньютона следует, что уравнение движения
перемычки в проекции на ось, направленную
параллельно шинам вниз, имеет вид
где а – проекция ускорения перемычки на указанное направление.
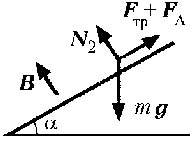
Рис. 3
Поскольку перемычка движется по шинам,
то величина нормальной составляющей силы
реакции шин N = mg cos . Если расстояние между
шинами обозначить L, а сопротивление перемычки R,
то, согласно правилу потока Фарадея–Максвелла и
закону Ома, сила тока, текущего по перемычке при
величине скорости её движения, равной 
1, должна быть
равна I1 = BL1/R, т.к., по условию задачи,
сопротивлением остальных элементов проводящего
контура и его индуктивностью следует пренебречь.
Учитывая, что индукция магнитного поля и
перемычка взаимно перпендикулярны, находим
величину силы Ампера: 
а затем из уравнения
движения получаем, что при установившемся
движении перемычки (т.е. при a = 0) величина её
скорости
В случае, когда внешнее магнитное поле
направлено вертикально, действующую на
перемычку силу Ампера, направленную
горизонтально, удобно представить в виде двух
компонент, одна из которых 
направлена параллельно шинам, а
другая 
–
перпендикулярно к ним, как показано на рис. 4.
Повторяя практически дословно приведённые выше
рассуждения, можно доказать, что при скорости
движения перемычки, равной 2, через перемычку должен
протекать ток 
При этом указанные
компоненты силы Ампера будут равны
и 
а уравнение движения перемычки в
проекции на направленную вниз параллельно шинам
ось будет иметь вид 
где 
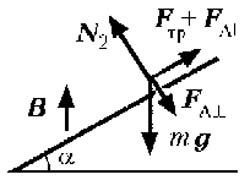
Рис. 4
Следовательно, в этом случае величина скорости установившегося движения перемычки при выполнении сделанных предположений равна
Если, как обычно, считать, что
коэффициент трения не превышает единицы, то из
полученных выражений следует, что 
а потому,
согласно условию задачи, 
и искомый коэффициент трения
Если же считать, что коэффициент
трения превышает единицу, что обычно не имеет
места, то 
, и искомая величина должна быть равна
