Продолжение. См. № 4, 6, 8, 10, 12, 16/05
6 Тонкое
проводящее кольцо радиусом r находится в
горизонтальном однородном магнитном поле
индукцией В, перпендикулярной его
плоскости. Подвижный проводник ОА, имеющий массу m
и достаточно большое сопротивление R, одним
концом шарнирно закреплён в центре кольца (точка
О), а другим (точка А) скользит по кольцу, как
показано на рис. 5. Найти закон, по которому должна
изменяться со временем ЭДС![]() (t) источника напряжения,
подключённого к точке О и кольцу, чтобы проводник
вращался с постоянной угловой скоростью
(t) источника напряжения,
подключённого к точке О и кольцу, чтобы проводник
вращался с постоянной угловой скоростью ![]() . Сопротивлением
кольца и трением пренебречь. Ускорение
свободного падения равно g.
. Сопротивлением
кольца и трением пренебречь. Ускорение
свободного падения равно g.
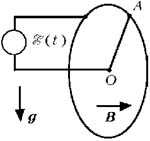
Рис. 5
Решение
По условию задачи, индуктивностью
контура, по которому протекает ток, следует
пренебречь. Другими словами, следует считать, что
индукция В внешнего магнитного
поля во много раз превышает индукцию магнитного
поля, порождаемого током во всех проводниках
контура. Как обычно, при решении задачи будем
считать, что кольцо и источник внешнего
магнитного поля покоятся относительно
лабораторной системы отсчёта и эту систему можно
считать инерциальной. Поскольку проводник ОА
тонкий и вращается с угловой скоростью ![]() вокруг оси
кольца, скорость упорядоченного движения
свободных носителей заряда в этом проводнике
относительно указанной системы отсчёта можно
представить в виде суммы двух векторов, один из
которых перпендикулярен оси проводника, а второй
направлен вдоль этой оси. Ясно, что обе эти
компоненты лежат в вертикальной плоскости, в
которой расположено кольцо.
вокруг оси
кольца, скорость упорядоченного движения
свободных носителей заряда в этом проводнике
относительно указанной системы отсчёта можно
представить в виде суммы двух векторов, один из
которых перпендикулярен оси проводника, а второй
направлен вдоль этой оси. Ясно, что обе эти
компоненты лежат в вертикальной плоскости, в
которой расположено кольцо.
Величина перпендикулярной компоненты
указанной скорости равна скорости движения той
точки проводника, в которой в данный момент
находится свободный носитель заряда, т.е. ![]() где ri
– радиус вращения интересующей точки проводника
ОА. Из-за наличия этой компоненты свободные
носители заряда испытывают действие магнитной
составляющей силы Лоренца
где ri
– радиус вращения интересующей точки проводника
ОА. Из-за наличия этой компоненты свободные
носители заряда испытывают действие магнитной
составляющей силы Лоренца ![]() эквивалентное действию
стороннего электрического поля Е1,
величина напряжённости которого равна
эквивалентное действию
стороннего электрического поля Е1,
величина напряжённости которого равна
![]()
т.к. скорость ![]() рассматриваемой точки и индукция В
магнитного поля взаимно перпендикулярны, а
направление Е1 (в
соответствии с правилом нахождения направления
магнитной составляющей силы Лоренца)
коллинеарно оси проводника ОА и образует правую
тройку векторов с векторами
рассматриваемой точки и индукция В
магнитного поля взаимно перпендикулярны, а
направление Е1 (в
соответствии с правилом нахождения направления
магнитной составляющей силы Лоренца)
коллинеарно оси проводника ОА и образует правую
тройку векторов с векторами ![]() и В. Из
приведённого соотношения видно, что величина
напряжённости стороннего электрического поля
прямо пропорциональна удалению рассматриваемой
точки проводника от оси вращения и не зависит от
времени, т.к. угловая скорость вращения и
индукция магнитного поля постоянны. Влияние
этого стороннего поля на силу тока в цепи, как
обычно, учтём, определив энергетическую
характеристику этого поля – его ЭДС. По
определению, величина ЭДС равна модулю отношения
работы сил стороннего поля над пробным зарядом
при его перемещении вдоль рассматриваемого
участка цепи к величине этого заряда. Учитывая,
что напряжённость сторонних сил направлена
вдоль оси проводника, можно утверждать, что
величина ЭДС на достаточно малом участке
проводника длиной
и В. Из
приведённого соотношения видно, что величина
напряжённости стороннего электрического поля
прямо пропорциональна удалению рассматриваемой
точки проводника от оси вращения и не зависит от
времени, т.к. угловая скорость вращения и
индукция магнитного поля постоянны. Влияние
этого стороннего поля на силу тока в цепи, как
обычно, учтём, определив энергетическую
характеристику этого поля – его ЭДС. По
определению, величина ЭДС равна модулю отношения
работы сил стороннего поля над пробным зарядом
при его перемещении вдоль рассматриваемого
участка цепи к величине этого заряда. Учитывая,
что напряжённость сторонних сил направлена
вдоль оси проводника, можно утверждать, что
величина ЭДС на достаточно малом участке
проводника длиной ![]() r
r
![]()
Поскольку длина проводника ОА равна r,
то он состоит из N = r/![]() r таких участков, ri
= i
r таких участков, ri
= i![]() r,
а потому величина интересующей ЭДС равна
r,
а потому величина интересующей ЭДС равна
![]()
Наличие продольной компоненты скорости упорядоченного движения носителей заряда, т.е. протекание тока по проводнику, находящемуся в магнитном поле, обуславливает появление сил Ампера. По условию задачи и сделанному выше предположению, проводник ОА вращается с постоянной угловой скоростью относительно инерциальной системы отсчёта. Следовательно, суммы действующих на него сил (силы тяжести, реакции оси и силы Ампера) и их моментов относительно любой оси должны быть равны нулю, т.к. силами трения следует пренебречь.
Чтобы упростить решение задачи, будем
рассчитывать действующие на проводник моменты
сил относительно оси вращения. При этом,
поскольку иное в условии задачи не оговорено,
будем считать проводник однородным. В тот момент
времени t, когда проводник образует с
горизонтальным диаметром кольца угол ![]() (рис. 6), момент силы
тяжести, действующей на малый отрезок проводника
ОА длиной
(рис. 6), момент силы
тяжести, действующей на малый отрезок проводника
ОА длиной ![]() r,
находящийся от оси вращения на расстоянии ri,
равен
r,
находящийся от оси вращения на расстоянии ri,
равен
![]()
т.к. масса такого отрезка ![]() mi = m
mi = m![]() r/r.
Следовательно, общий момент сил тяжести,
действующих на проводник, равна
r/r.
Следовательно, общий момент сил тяжести,
действующих на проводник, равна
![]()
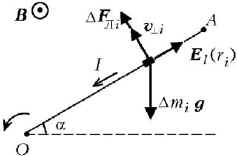
Рис. 6
Учитывая, что проводник ОА движется в
вертикальной плоскости, перпендикулярной линиям
индукции внешнего магнитного поля, на основании
закона Ампера можно утверждать, что на i-й
участок проводника длиной ![]() r действует сила, величина
которой равна
r действует сила, величина
которой равна
![]()
где I(t) – сила тока, текущего по этому участку проводника в момент времени t. Повторяя почти дословно рассуждения, приведшие к вычислению момента сил тяжести, и учитывая, что сила Ампера направлена перпендикулярно оси проводника и индукции внешнего поля, можно показать, что величина момента сил Ампера, действующих на проводник ОА относительно оси вращения, равна
![]()
Согласно сказанному выше, сумма моментов силы Ампера и силы тяжести относительно оси вращения должна быть равна нулю. Следовательно, сила тока, текущего по проводнику ОА, должна изменяться по закону
![]()
причём ток I в проводнике ОА при показанных на рис. 6 направлениях вращения и индукции магнитного поля должен течь в направлении, указанном на этом рисунке серой стрелкой.
По условию задачи, сопротивлением кольца, контактов и индуктивностью контура следует пренебречь. Ток в контуре создаёт источник напряжения, т.е. источник, внутреннее сопротивление которого равно нулю. Равным нулю будем считать и сопротивление проводов, соединяющих источник с остальными элементами. Поэтому, согласно закону Ома, с учётом сказанного в конце предыдущего абзаца и направления магнитной составляющей силы Лоренца искомая ЭДС источника напряжения равна
![]()