. Пренебрегая трением, найдите величину
силы, с которой стержень действует на верхний
шарик, и угол 
, который эта сила составляет с
вертикалью.6
Жёсткий невесомый стержень шарнирно прикреплён
одним концом к потолку. На другом конце и на
середине стержня закреплены маленькие шарики
массой m каждый. Стержень вращается с постоянной
угловой скоростью, образуя с вертикалью
постоянный угол . Пренебрегая трением, найдите величину
силы, с которой стержень действует на верхний
шарик, и угол , который эта сила составляет с
вертикалью.
Решение
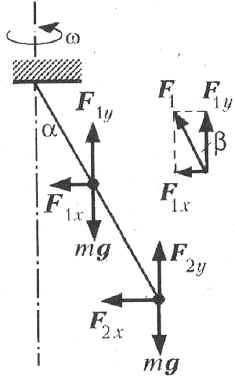
Рис. 6
При решении задачи будем считать
лабораторную систему отсчёта, относительно
которой потолок неподвижен, инерциальной. Пусть
длина стержня равна 2L. Поскольку стержень
образует с вертикалью постоянный угол и, по условию
задачи, размерами шариков следует пренебречь, то
радиусы окружностей, по которым движутся первый
и второй шарики, равны соответственно R1
= Lsin и R2
= 2Lsin (рис.
6). По условию задачи, трением, в том числе и силами
сопротивления движению тел системы, следует
пренебречь. Следовательно, на шарики действуют
только силы тяжести и силы реакции стержня. Если
постоянную угловую скорость вращения стержня
обозначить 
и учесть, что шарики не перемещаются в
вертикальном направлении, то, согласно второму
закону Ньютона, величины вертикальных
составляющих сил реакции стержня F1y
и F2y на первый и второй шарики
должны быть равны mg, где g – величина
ускорения свободного падения, а горизонтальные
составляющие указанных сил равны соответственно
F1x=m2R1 и F2x=m2R2,
т.к. центростремительные ускорения шариков aix
= 2Ri.
На рис. 6 наряду с силами тяжести mg показаны
действующие на шарики силы реакции стержня F1
и F2, а также составляющие
этих сил Fix и Fiy
в тот момент, когда стержень с шариками
располагается в плоскости рисунка.
По условию задачи, массой стержня следует пренебречь. Поэтому сумма действующих на стержень сил и сумма моментов этих сил должны быть равны нулю. Как известно, при выполнении первого условия сумма моментов сил не зависит от выбора конкретной оси вращения. Поэтому, чтобы не вычислять силу, действующую на стержень со стороны шарнирного подвеса, второе условие целесообразно записать относительно оси, проходящей через точку подвеса стержня к потолку перпендикулярно плоскости рисунка. Поскольку сила, действующая на шарик со стороны стержня, согласно третьему закону Ньютона равна по величине и противоположна по направлению силе, с которой шарик действует на стержень, и величина момента силы относительно заданной оси равна произведению плеча силы на величину этой силы, то
Подставляя в это уравнение найденные ранее значения составляющих сил реакции стержня на шарик, находим, что
а потому величина силы, с которой стержень действует на верхний шарик,
и эта сила образует с вертикалью (см. рис. 6) угол
7 Тонкостенный отрезок трубы массой m, начав скатываться без скольжения с вершины закреплённого на горизонтальной плоскости полуцилиндра радиусом R, оторвался от его поверхности, опустившись вниз на расстояние h (рис. 7). При скатывании ось трубы оставалась горизонтальной. Зная, что радиус трубы много меньше R, найдите работу А сил сопротивления движению трубы за время её движения по полуцилиндру.
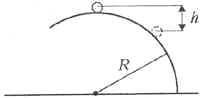
Рис. 7
Решение
При решении задачи будем, как обычно,
считать закреплённый цилиндр неподвижным
относительно лабораторной системы отсчёта, а эту
систему будем считать инерциальной. Поскольку
труба скатывается без проскальзывания, то
величины скорости 
оси трубы и угловой
скорости её вращения вокруг этой оси
удовлетворяют соотношению 
где r – радиус
трубы. Следовательно, скорость i-й точки
трубы равна 
где 
– скорость этой точки относительно оси
трубы, т.к. ось трубы не изменяет своего
направления относительно лабораторной системы
отсчёта (рис. 8). По условию задачи, труба является
тонкостенной. Следовательно, для любой её точки
можно считать, что 
Поскольку иное в условии
задачи специально не оговорено, будем считать
трубу однородной. Поэтому кинетическая энергия
катящейся без проскальзывания тонкостенной
трубы массой m должна быть равна
т.к. массы диаметрально
противоположных одинаковых по размерам малых
участков трубы mi в силу её однородности равны, а
их скорости, обусловленные вращением трубы
вокруг своей оси, равны по величине но направлены в
противоположные стороны.
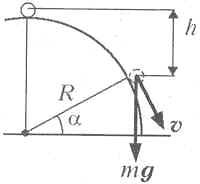
По закону изменения механической
энергии изолированной системы
полуцилиндр–Земля–труба 
где g – величина
ускорения свободного падения. На рис. 8 исходное
положение трубы изображено сплошной линией, а её
положение в момент отрыва от полуцилиндра –
пунктиром. В момент отрыва трубы сила реакции
опоры обращается в нуль, а сила сопротивления
движению трубы направлена антипараллельно
скорости движения её оси*. (*Утверждая это, мы
предполагали, что вращающаяся при скатывании
труба не вовлекает во вращение прилегающие к ней
слои воздуха.) По условию задачи, радиус трубы r
много меньше радиуса R полуцилиндра, поэтому
можно считать, что ускорение центра масс трубы
равно 
и оно обеспечивается составляющей силы тяжести,
равной mgsin
= mg(R – h)/R. Следовательно,
согласно второму закону Ньютона, в момент отрыва
трубы должно выполняться соотношение
а потому искомая работа сил сопротивления движению трубы равна A = mg(R – 2h).
Поскольку работа сил сопротивления не
может быть величиной положительной, то при
выполнении сделанных при решении задачи
предположений полученный ответ верен, если 
При h=0,5
R, согласно полученному ответу, на трубу во время
её скатывания не должны были действовать ни силы
сопротивления со стороны воздуха, ни силы трения
качения. Если же 
или 
то условие задачи
противоречиво.
8 На
внутреннюю поверхность полусферы радиусом R,
закреплённой так, что её ось симметрии
вертикальна, концом А опирается тонкая гладкая
однородная палочка так, как показано на рис. 9. При
этом палочка касается края полусферы в некоторой
точке В и образует с горизонтом угол =30°. Найдите длину L
палочки.
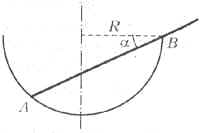
Рис. 9
Решение
По условию задачи, полусфера неподвижна относительно лабораторной системы отсчета. Считая эту систему инерциальной, можно утверждать, что при равновесии гладкая палочка должна располагаться в вертикальной плоскости, проходящей через центр полусферы, т.к. на неё со стороны полусферы не могут действовать силы трения, а потому силы реакции полусферы на палочку могут быть направлены только по нормалям к границам раздела.
На рис. 10 показано сечение полусферы
вертикальной плоскостью, проходящей через её
центр О, и сила тяжести mg, где m – масса
палочки, а g – ускорение свободного падения.
На этом же рисунке в соответствии со сказанным
показаны силы NА и NВ
реакции полусферы на палочку. Поскольку
треугольник АОВ равнобедренный и сила NА
направлена вдоль радиуса АО, то она образует с
горизонтом угол 2, а сила NВ направлена
под углом к
вертикали.
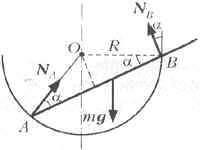
Рис.10
Как известно, при равновесии ускорение центра масс твёрдого тела относительно инерциальной системы отсчёта должно быть равно нулю. Кроме того, должно быть равно нулю и угловое ускорение этого тела относительно любой оси вращения, неподвижной относительно инерциальной системы отсчёта. Из первого условия следует, что сумма действующих на тело сил должна быть равна нулю, т.е. должны выполняться соотношения:
Угловое ускорение твёрдого тела будет равно нулю, если алгебраическая сумма моментов сил, действующих на тело, относительно произвольной неподвижной оси будет равна нулю. Поскольку действующие на палочку силы лежат в одной вертикальной плоскости, а при равенстве суммы сил нулю величина алгебраической суммы моментов сил относительно всех параллельных друг другу неподвижных осей одинакова, условие равенства нулю углового ускорения палочки запишем в виде равенства нулю суммы моментов силы тяжести и силы NВ относительно оси, проходящей через точку А перпендикулярно плоскости рис. 10:
При составлении этого соотношения
было учтено, что длина части палочки АВ равна 2Rcos, а величина
момента силы равна произведению плеча силы на
величину этой силы.
Из трёх последних соотношений следует, что
а потому искомая длина палочки
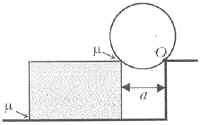
9 На
горизонтальной плоскости на расстоянии а от
закреплённой ступеньки лежит брусок. Высоты
ступеньки и бруска одинаковы. На ребро бруска,
параллельное краю ступеньки, опирается цилиндр
(рис. 11), который может без трения вращаться
вокруг оси О, прикреплённой к краю ступеньки.
Массы бруска и цилиндра равны. Если 
где R –
радиус цилиндра, то брусок покоится, а если 
то
брусок скользит, не отрываясь от плоскости.
Считая коэффициент трения m между всеми
трущимися поверхностями одинаковым, найдите
величину 
.
Решение
По условию задачи, ступенька и горизонтальная плоскость, на которой лежит брусок, неподвижны относительно лабораторной системы отсчёта. Будем, как обычно, считать эту систему инерциальной.
На рис. 12 показано сечение бруска, ступеньки и цилиндра вертикальной плоскостью, перпендикулярной оси цилиндра и проходящей через его центр масс. На этом же рисунке показаны силы тяжести mg, действующие на брусок и цилиндр, где m – масса цилиндра, равная, по условию задачи, массе бруска, а g – ускорение свободного падения. Силы реакции плоскости на брусок (N1 и Fтр1), цилиндра на брусок (N2 и Fтр2) и бруска на цилиндр (N3 и Fтр3) изображены на рис. 12, каждая в виде двух составляющих. Одна из этих составляющих (Ni) направлена по нормали к границе соприкосновения – нормальная составляющая силы реакции опоры, а другая (Fтрi) – тангенциальная составляющая – перпендикулярна первой и направлена в сторону, противоположную тому направлению, в котором начало бы двигаться данное тело, если бы эта составляющая стала равной нулю.
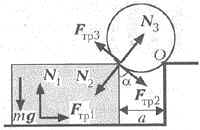
Рис. 12
По условию задачи, брусок и цилиндр
находятся в равновесии, если расстояние между
вертикальной гранью бруска, ближайшей к
ступеньке, и ступенькой где R – радиус цилиндра.
Следовательно, можно считать, что при 
величины сил
сухого трения покоя становятся максимальными, а
потому, согласно закону Кулона–Амонтона, их
величины равны произведению коэффициента трения
на величину соответствующей нормальной
составляющей силы реакции, причём в соответствии
с третьим законом Ньютона N2=N3
и Fтр2=Fтр3=N2.
Обратившись к рис. 12, легко убедиться,
что при угол
между нормальной составляющей N2 силы
реакции цилиндра на брусок и горизонтом
удовлетворяет условию 
Поскольку при этом брусок ещё остаётся неподвижным относительно инерциальной системы отсчёта, то, согласно второму закону Ньютона,
и 
а потому 
Согласно правилу моментов, записанному относительно оси, на которой закреплён цилиндр, условие его равновесия можно представить в виде:
С учётом ранее полученных соотношений
из этого уравнения следует, что 
Решая это уравнение и учитывая, что коэффициент трения является величиной неотрицательной, находим искомое значение этого коэффициента
10 К концам нерастяжимой нити, перекинутой через три гладких блока, прикреплены пружины жёсткостью k1 и k2 так, как показано на рис. 13. При этом отрезки нити, не лежащие на блоках, вертикальны, а оси пружин совпадают с прикреплёнными к ним вертикальными отрезками нитей. К оси лёгкого подвижного блока на нити подвешен груз массой m. Пренебрегая массой нитей и пружин, найдите максимальную амплитуду А вертикальных гармонических колебаний груза.
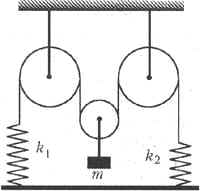
Решение
Как обычно, будем решать задачу, полагая плоскости, к которым прикреплены блоки и пружины, неподвижными относительно лабораторной системы отсчёта, которую, в свою очередь, будем считать инерциальной. Поскольку блоки гладкие, то нить, соединяющая пружины, будет скользить по блокам, не вызывая их вращения. По условию задачи, следует рассматривать вертикальные колебания груза, а потому следует считать, что длины отрезков нити, лежащих на блоках, не будут изменяться при движении груза, т.к. другие отрезки этой нити, по условию задачи, при неподвижном грузе были вертикальны. Сказанное, очевидно, верно, если считать, что при колебаниях подвижный блок не поднимается столь высоко, что он может коснуться хотя бы одного неподвижного блока.
Из того, что между нитью, связывающей пружины, и блоками не действуют силы трения и нить, по условию задачи, невесома, следует, что величина F силы натяжения этой нити во всех её точках должна быть одной и той же. По условию задачи, массой подвижного блока следует пренебречь. Будем пренебрегать и силами сопротивления движению тел системы со стороны воздуха, т.к., по условию задачи, колебания груза, по крайней мере при достаточно малых амплитудах, должны быть гармоническими. Поэтому можно считать, что сумма сил, действующих на подвижный блок со стороны нитей, равна нулю как в положении равновесия, так и при движении груза, т.е. выполняется соотношение 2F=T, где Т – величина силы натяжения нити, прикреплённой к оси блока. Учитывая невесомость этой нити, можно утверждать, что со стороны этой нити на груз действует сила 2F, направленная вертикально вверх, т.к. нить не может толкать груз вниз. Следовательно, считая нить, с помощью которой груз крепится к оси подвижного блока, нерастяжимой, согласно второму закону Ньютона, уравнение движения груза в проекциях на направленную вертикально вниз ось ОХ выбранной инерциальной системы отсчёта можно записать в виде
где 
– проекция ускорения груза на указанную
ось, а g – величина ускорения свободного
падения.
*Здесь, как это и принято в физике, производные функций по временим обозначены с помощью надлежащего числа точек, поставленных над символом этой функции.
Из сказанного выше следует, что 
а при
равновесии F=0,5mg. Из последнего
утверждения, если учесть равенство величин сил, с
которыми связывающая пружины нить действует на
них, в соответствии с законом Гука следует, что
величины деформаций 
пружин при равновесии должны
удовлетворять условию
Поскольку в условии задачи специально
не оговаривается иное, будем считать нити, с
помощью которых неподвижные блоки прикреплены к
верхней плоскости, нерастяжимыми. Тогда, с учётом
сделанных выше предположений, можно утверждать,
что при смещении груза вниз от положения
равновесия на величину 
и увеличении длины первой
пружины на 
длина второй пружины должна увеличиться
на 
если нить остаётся натянутой, т.е. если F>0.
При колебаниях груза разные части
пружин будут двигаться с разными ускорениями, а
потому в общем случае сила натяжения пружин в
разных их точках должна быть разной. Если же
пренебречь массами пружин, как то и предлагается
в условии задачи, то можно считать, что и при
движении груза деформации пружин и вызывающие их
силы подчиняются закону Гука. Следовательно, при
малых колебаниях груза, когда он сместится от
положения равновесия на величину , силы натяжения
пружин должна возрасти на одну и ту же величину 
где и 
–
дополнительное растяжение первой и второй
пружин, причём + = 2. Учитывая равенство 
и
полученные выше соотношения, преобразуем
уравнение движения груза следующим образом:
Как известно, решение этого уравнения имеет вид
где амплитуда А и фаза колебаний 
определяются
начальными условиями, а угловая частота
колебаний 
Поскольку при таких колебаниях
амплитуда ускорения 
не должна превышать g (в
противном случае нить должна была бы толкать
груз вниз), то искомая максимальная амплитуда
колебаний груза при выполнении сделанных при
решении задачи предположений равна
