Продолжение. См. № 17, 18, 19, 20, 21, 22/06

А.А.КНЯЗЕВ,
ЛПН, г. Саратов
knf@sgu.ru

Олимпиадный материал в повседневной работе преподавателя физики

Лекция 7. Электромагнитные явления

Введение

Школьные формулы для магнитного поля необычны и пугают своей изощрённостью – буравчики, разные руки – проще запомнить, чем разбираться. А закон индукции Фарадея являет вообще физику новой формы материи – физику электромагнитного поля. Пожалуй, трудно даже сказать, какие из представлений – полевые или квантовые – сложнее для человеческого сознания.

В школе всё это сложно ещё и потому, что в большинстве учебников последовательность изложения в этой части следует очень старой схеме начала прошлого века – так учились во времена юности Эйнштейна. Когда-то другой схемы не было, да и вполне логично начинать знакомство с магнитными явлениями наблюдением взаимодействия двух магнитов и действия на магнитную стрелку как земного магнетизма, так и проводника, по которому пропускают сильный ток. Однако сейчас, для способного школьника в современном мире этого может хватить разве что на программу 7–8-го классов. Для старших классов физматшкол необходимы численные оценки по вполне обоснованным соотношениям. Тем не менее можно привести, пожалуй, лишь один сборник школьных задач, охватывающий весь спектр электромагнитных явлений [1]. Дело не в злонамеренности авторов учебников – сложные явления требуют для описания своих моделей большей степени абстракции. Так устроена Природа.

Магнитное взаимодействие. Физическая причина

Ровным счётом век понадобился науке для понимания, что магнитная сила не отражает нового фундаментального взаимодействия. Она описывается не исключительно эмпирическими формулами, а проявляется при движении зарядов как вполне просчитываемый эффект. При малых скоростях движения зарядов относительно наблюдателя магнитная сила является пренебрежимо слабой релятивистской добавкой к кулоновской силе. При скоростях движения зарядов, близких к скорости света, влияние магнитной силы приближается к силе электростатического взаимодействия. Теперь деление поля на электрическое и магнитное приобретает относительный смысл. Например, периодическое магнитное поле может быть воспринято быстро движущимся зарядом как поле электрических колебаний. Наконец, в явлении электромагнитного излучения электрическая и магнитная составляющие становятся равноправными, образуя единое электромагнитное поле [2].

Процедуру введения главной характеристики магнитной силы – магнитной индукции – можно проиллюстрировать следующим упрощённым выводом1. Не будем отвлекаться на изложение релятивистской теории. У современной школы есть превосходная возможность дать школьникам представления теории пространства-времени [3, 4]. Здесь для нас главное в том, что с точки зрения неподвижного наблюдателя сила взаимодействия двух зарядов, движущихся параллельно друг другу, отличается от кулоновской силы Fq и выражается как 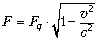. Следуя [3], умножим и разделим выражение на релятивистский корень, и затем пренебрежём малыми слагаемыми в числителе2. Получим . 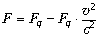Видно, что взаимодействие между движущимися зарядами ослабевает. Можно, однако, сказать иначе: на движущиеся заряды кроме силы Кулона действует дополнительная сила, описываемая вторым слагаемым в предыдущей записи, – это и есть магнитная сила. Для точечных одноимённых зарядов её можно записать как

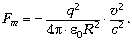
Вернёмся к основному выражению, в котором появляется магнитная сила:

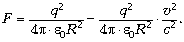
Если мы имеем дело с системой не двух, а многих зарядов, удобно выделить напряжённости сил системы. Так, первое слагаемое принимает известную уже форму по следующей схеме:

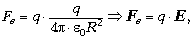
где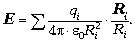

А вот с магнитной силой значительно сложнее, ведь она зависит не только от расположения частиц, но и от скоростей. Вначале можно выделить заряд и скорость пробной частицы. Сделаем это в простейшем, скалярном виде, не обобщая на сложные случаи:

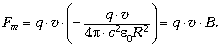
Введённая этим соотношением величина 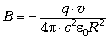, по сути, представляет модуль силы, действующей на единичную пробную частицу, движущуюся с единичной скоростью, со стороны другой частицы. Это и есть индукция магнитной силы. Сейчас её записывают в форме 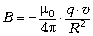, вводя ещё одну физическую постоянную3  

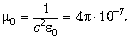
Видно, что при 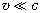магнитная добавка, пропорциональная 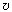2/c2 ~ 10–20, ничтожна по сравнению с кулоновской силой. Поэтому во всех случаях движения с малыми скоростями ею, безусловно, можно пренебрегать, если эти силы придётся сравнивать.

Однако среди других магнитных явлений особое место занимает взаимодействие проводников с током. Здесь слабый релятивистский эффект проявляется как вполне макроскопическое явление. Рассмотрим это уникальное явление на примере следующей задачи.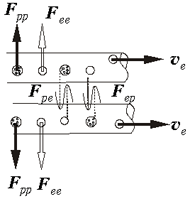

  • Оцените магнитную силу для двух близких металлических проводников с концентрацией электронов n ~ 1028 м–3, длиной ~1 м и сечением ~1 мм2 при однонаправленных токах порядка 1 А.

Решение. Металлические проводники, как и большая часть других, не заряженных тел, представляют собой ансамбли частиц, в которых электрическая сила расталкивания одноимённо заряженных частиц с высокой точностью скомпенсирована электрической силой притяжения частиц противоположного знака – число протонов в веществе практически равно числу электронов. Главное сейчас в том, что скомпенсированные электростатические силы расталкивания и притяжения огромны по модулю. Их величину для двух отрезков проводников длиной L, находящихся на расстоянии R, оценим по формуле закона Кулона:

.

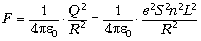По порядку величины4  получим 1018 Н. Это огромные, трудно представимые силы. Тем не менее положительные заряды остова кристаллической решётки металлов остаются, в среднем, неподвижными, поскольку электроны, препятствующие разлёту протонов, тоже, в среднем, покоятся.

При возникновении в проводниках тока – направленного движения свободных (валентных) электронов – ситуация нарушается. Для тока порядка 1 А это движение электронов происходит со скоростью 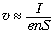, которая составляет долю миллиметров в секунду, тогда как ионы, в среднем, так и остаются на месте. Кажется невероятным, что эта лёгкая асимметрия может привести к значительному эффекту. Однако это так. Поскольку главные силы скомпенсированы, то нарушение существующего равновесия приводит к возникновению их разности, той самой нескомпенсированной силы, составляющей ~ 10–20 от величины любой из кулоновских сил. Вычислив эту малую долю от огромного значения основной силы 1018 Н, получаем, что магнитная сила имеет вполне измеряемую в макроскопических масштабах величину: в нашем случае ~10–2 Н. С такой силой притягиваются параллельные токи.

Вот и всё в основных чертах5. Магнитная сила проявляется в опытах Ампера, в работе электрических двигателей (эффект многократно усиливается за счёт большого числа проводов в обмотке). Так же, как и кулоновская, магнитная сила тоже направлена по прямой, соединяющей взаимодействующие заряды, и оценивается по кулоновской схеме.

Жаль, что часто изучение релятивистской теории в школе не связано с темой электромагнетизма. Ни по времени, ни по смыслу. В результате практически теряется смысл знакомства с этой теорией вообще. В самом деле эффект выделения энергии при перестройке связей в ядре может быть проиллюстрирован по аналогии с опытом разрядки конденсатора – без использования соотношения массы и энергии. Если же говорить об интересных явлениях вообще, то почему выбор падает именно на эффекты теории относительности?

Теперь, когда природа магнитных сил выявлена, обсудим те самые, трудно запоминаемые, инженерные формулы теории магнетизма. Интересно, что эти формулы оформились уже тогда, когда магнитные явления и без них входили в практику (реле, телеграф).

Магнитное взаимодействие. Математическая модель

На сегодняшний день в теории магнетизма – магнитостатике – выделяют следующую логическую схему: 1) по заданной конфигурации тока рассчитывается вид поля вектора магнитной индукции B; 2) зная это поле, можно вычислить силу, действующую на частицу (записать уравнение движения) или вычислить силу, действующую на ток заданной формы, внесённый в поле B, и решить задачу о движении этого тока или частицы.

Исторически эта обозначенная схема формировалась причудливо и очень трудно. Основываясь всего на двух экспериментах, А.-М.Ампер посредством размышлений получил формулу для описания взаимодействия элементов двух токов, но ему пришлось воспользоваться эмпирическими коэффициентами. Не располагая современной теорией относительности, учёные пытались получить уже записанные нами формулы для расчёта силы взаимодействия движущихся зарядов. В.Вебер (ок. 1870) разработал теорию, однако и она требовала дополнительных данных и приводила к бесконечностям в случаях предельных переходов к покоящимся зарядам. Интегральные формулы, полученные Ж.Био, Ф.Саваром и П.Лапласом для расчёта магнитной индукции, тоже содержали коэффициенты, определить которые можно лишь экспериментально.

Современные формулы были получены Дж.Максвеллом лишь к середине XIX в. Выручил М.Фарадей, высказавший мысль о полях электрических и магнитных линий вокруг тока (1851). Трудно сказать, как это получилось в точности, – возможно, при наблюдении за расположением железных опилок вместо магнитных стрелок в опытах Ф.Араго и Т.Зее-бека, повторивших опыты Эрстеда. Линии Фарадея позволили использовать возникавший в это время математический аппарат векторного анализа (У.Гамильтон, Г.Грассман, В.Вебер, Г.Риман, Г.Герц, В.Гиббс). Отметим важную разницу между линиями электрического и магнитного полей. Линии напряжённости электрического поля вполне можно называть силовыми – касательные к ним определяют направление силы. Линии магнитной индукции, в современном смысле, не являются силовыми – они не указывают направления силы, поскольку для этого необходимо знать ещё и вектор скорости. Здесь часто возникают недоразумения, поскольку сам Фарадей называл все линии силовыми, по-видимому, на том основании, что они используются в описании силы.

Формула Био–Савара–Лапласа

Известная формула, позволяющая определить значение модуля элементарного вектора магнитной индукции 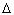B, создаваемой элементарным отрезком 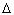L тока I в точке, отстоящей на расстоянии R от этого тока (приводим её без графического пояснения, имеющегося в различных учебниках):

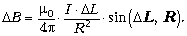
По структуре она похожа на приведённую выше формулу для поля точечного заряда. Достаточно только произведение q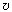 выразить посредством известной уже формулы I = en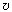S и учесть, что q = enS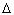L. А вот появление синуса вместо знака «минус» примем без обсуждения – это от теории векторной алгебры.

В школе направление вектора 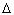B определяют по правилу буравчика, или правого винта, также следующему из векторной теории. Для расчёта полного значения и направления вектора B в данной точке от всей конфигурации тока элементарные значения векторно складывают. Так получаются известные формулы для решения стандартных задач. Приведём их.

1. Легко получается формула значения магнитной индукции в центре кругового витка с током. Действительно, если сложить все элементарные векторы в центре витка, то запись примет вид:

.

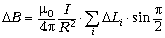Отсюда получается 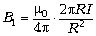. Мы не производим очевидные сокращения, чтобы в памяти отложилась удобная для запоминания структура формулы, связанная с основной. Так, используя результат предыдущей лекции с расчётом тока валентного электрона, можно оценить поле валентного электрона на ядре атома водорода – не менее 1 Тл. Кабель с током порядка 10–100 А, уложенный по периметру корабля, нейтрализует поле, наведённое в его металлическом корпусе земным магнетизмом (около 10–4 Тл), и спасает от магнитных мин (И.В.Курчатов, 1939).

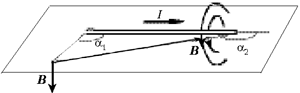
2. Расчёт магнитной индукции от отрезка прямого тока в точке, расположенной на расстоянии r от прямой, требует более кропотливой процедуры интегрирования. В результате получаем

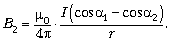
Выбор углов 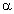1 и 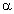2 иллюстрируется рисунком.

3. Приведём и третью, важную формулу – для индукции внутри соленоида (тонкой, но очень длинной катушки без сердечника):

B3 = 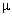0In,

здесь n – число витков на единицу длины. Ближе к краю индукция спадает, вне соленоида значение индукции пренебрежимо мало, а в целом структура поля напоминает поле стержневого постоянного магнита.

4. Для прочих конфигураций значение индукции пропорционально силе тока и обратно пропорционально характерному для данной задачи размеру:

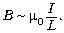
Формула Лоренца, формула Ампера

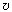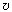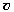Вторая часть программы расчёта магнитных взаимодействий связана с уже знакомой формулой. Первая формула – Fm = qB – записана Г.Лоренцем. Он ближе других подошёл к идеям релятивизма, его формулы часто смешивают с формулами Эйнштейна. Эту формулу мы получили исходя из релятивистской теории. Для общего случая расположения векторов запись чуть сложнее: Fm = Bsin(, B).

Формула определяет силу, которая действует на заряд, движущийся в уже созданном магнитном поле. Для определения направления силы, действующей на положительный заряд, в школе используют правило левой руки. В научной литературе формула записывается в виде векторного произведения, связанного с правосторонней тройкой векторов:

Fm = q[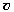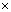B].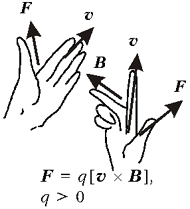

Сравним оба правила на схематическом рисунке. Видно – результат один и тот же. Преимущества второго состоят в универсальности записи, распространяющейся на другие подобные случаи работы с векторными величинами. В механике, например, на описание динамики вращательного движения. Формула Био–Савара–Лапласа тоже может быть записана в этой форме:

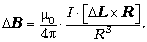
Очень удобно – без рук и буравчиков.

В случае, когда нужно определить силу, действующую со стороны магнитного поля не на заряд, а на участок длиной 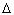L с током I, достаточно в предыдущей формуле выразить произведение q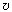 через ток, как это было сделано в предыдущем разделе. Получим формулу для силы Ампера: 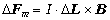. Отсюда следует, например, что если поле В создаётся прямолинейным током I1 и действует на параллельный этому току прямолинейный ток I2, то модуль силы взаимодействия на участке длиной L будет определяться формулой

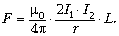
Это и есть формула Ампера для параллельных токов6.

Далее – электродинамика

Всё описанное ранее, казалось бы, укладывается в динамику Ньютона. Электрическая сила направлена по прямой линии, соединяющей взаимодействующие тела, и убывает по квадратичному закону (для точечных тел). Но это не так – вспомним попытки гениального Вильгельма Вебера: необходим учёт запаздывания взаимодействия.

  • На рисунке выделены два фрагмента токов. Определите силу взаимодействия этих отрезков в этой конфигурации.

К решению. Простая задача ставит в тупик. Сила со стороны второго тока стремится сдвинуть первый ток вниз. А вот сила со стороны первого тока для центральной части фрагмента второго тока равна нулю, а если взять конечную длину, то налицо стремление повернуть участок тока в плоскости рисунка по часовой стрелке. Выходит, изложенные выше правила определения силы нарушают третий закон Ньютона. Или его формулировка нуждается в уточнении.

Подобные недоумения возникают уже при попытке осмыслить действие закона притяжения Земли и Солнца, когда свет идёт между быстро движущимися взаимодействующими телами около 8 мин, – за это время конфигурация изменяется. Только слабость взаимодействия отвлекает нас от углубления в проблему. А здесь силы вполне осязаемые.

Вводя представления о линиях, Фарадей писал: «При этой точке зрения на магнит среда или пространство, его окружающее, играют столь же существенную роль, как и самый магнит, будучи частью настоящей и полной системы магнетизма». В теории Эйнштейна это положение получило формальное описание посредством введения пространства-времени. В этой теории, по сути, постулируется, что взаимодействие распространяется со скоростью света7 . При этом значение импульса одной взаимодействующей частицы запаздывает от такого же по величине значения импульса другой частицы на промежуток времени 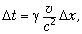и сумма механических импульсов оказывается не равной нулю в каждый момент времени. Значит, третьим участником взаимодействия в представлении о близкодействующем взаимодействии является силовое поле, забирающее импульс от одной частицы и переносящее его к другой. Силовое поле – не только математический объект, оно материально – обладает импульсом и энергией. Формулы плотности энергии в школе известны [3]. Так, в комнате на кубический метр приходится энергия примерно 10–7 Дж от поля Земли и проводов электропроводки и около 10–17Дж от TВ-каналов и мобильников.

  • Оцените вес груза, который можно поднять электромагнитом, сделанным из тысячи витков провода (d = 0,5 мм), намотанного на длине 10 см на толстый гвоздь, и питаемым батарейкой 3–4 В.

Решение. Проведём максимальную оценку. Сопротивление провода очень мало (около 0,1 Ом), поэтому ток от батарейки определяется лишь её внутренним сопротивлением и кратковременно может составить до 1 А (ток короткого замыкания). Это даёт значение магнитной индукции внутри сердечника до 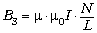~ 40 Тл и плотность энергии порядка 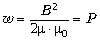~ 20 атм. На площади 0,3 см2 такое давление магнитной силы8  создаёт силу до 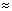60 Н.

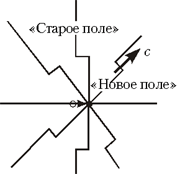
Излом линий – поперечное поле – излучение
Излом линий – поперечное поле – излучение

Представление Фарадея о материальности поля проявилось в открытии явления электромагнитной индукции 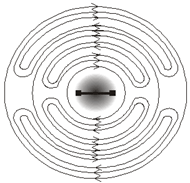и было воспринято как новый закон природы. Его содержание было уточнено Максвеллом и сформулировано как закон возникновения вихревого электрического поля в пространстве, где изменяется магнитное поле, т.е. когда заряд движется с ускорением, например, перемещается коротким скачком (см. излом силовой линии на рисунке [4]). Это часть поля совершенно нового типа. Его силовые линии изломаны, т.е. поле действует на другие заряды по иным, неньютоновским, законам – поперечно. Оно и есть переносчик взаимодействия. Для иллюстрации приведём мгновенный рисунок линий электрического поля вокруг колеблющегося диполя (например, антенны мобильника, телевизора). Линии поля замкнуты в отличие от статического диполя, имеют в направлении, перпендикулярном оси диполя, наибольшую густоту с периодическим изменением направления. Со временем конфигурация поля расширяется, наращиваются новые «слои», захватывается пространство и уносится энергия источника, который сообщает зарядам диполя колебательное движение. Скорость переноса энергии источника поля (групповая скорость) в пустоте определяется в любой системе отсчёта формулой 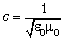. Описанный процесс переноса взаимодействия называется излучением электромагнитных волн, а длина пространственного периода называется длиной волны. Для мобильника это примерно 30 см. В такт разговору длина волны (и вся изображённая картинка) немного «подрагивает» (частотная модуляция – FM). Заштрихованная область около центра (радиусом около 15 см) сложна для изображения (здесь ещё сильно статическое поле диполя).

Силы вихревого поля могут совершать ненулевую работу по замкнутому контуру. Для них теряет смысл понятие потенциала. Такие поля частотами от 109 Гц до 1015 Гц управляют взаимодействием атомов при химических реакциях. Это и есть главные сторонние силы, о которых идёт речь в законе Ома. Те же силы работают в двигателях и генераторах.

  • Задача о синхротроне. Внутри соленоида (n = 1000 вит./м), на расстоянии R = 5 см от оси, покоится электрон. Оцените начальное ускорение при пропускании по соленоиду нарастающего тока
    I = 8t А.

Решение. Напряжённость вихревого электрического поля, возникшего в области нахождения электрона, определится из выражения для эдс индукции (работа силы в контуре с магнитным полем, отнесённая к заряду):

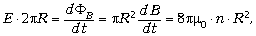
тангенциальное ускорение 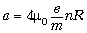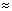1,2 • 107 м/с2.

Вот какие результаты даёт анализ релятивистской теории, правильно учитывающей динамические процессы взаимодействия тел на расстоянии. История физики шла куда более извилистым путём. Можно изумляться зоркости учёных XIX в., получавших практически те же результаты, да ещё и внедряя их по ходу открытий. И нигде не ошиблись!

Задач очень много. Часто они математически сложны. Но процесс излучения может быть не главным в рассматриваемом явлении. Так, при малых ускорениях зарядов (иначе: когда длина волны излучения превышает размеры устройства) излучением, как процессом потери энергии с участием неконсервативных сил, можно пренебречь. Например, при частоте 50 Гц длина волны составляет 6000 км (а при частоте 10 ГГц – 3 см). Тогда уравнения электродинамики превращаются в уравнения Кирхгофа. Запишем их для электрических цепей:

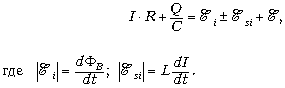
Знак «минус» относится к режиму двигателя (в случае движения контура в магнитном поле), а «плюс» – к режиму генератор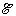а. – гальваническая эдс. Теперь можно вернуться к посильным для школы задачам о потенциалах (медленно меняющихся, чаще синусоидальных) и токах. В них – конденсаторы и катушки, переходные процессы, поле в веществе и пр. А эта лекция заканчивается по причине ограниченного объёма.

Вопросы для самоконтроля

1. Составьте таблицу характерных значений электрической напряжённости и магнитной индукции для широко известных явлений.

2. По аналогии с задачей о подъёмной силе магнита составьте формулу для плотности энергии сжатого стержня или колонны.

3. Возможен ли ток в разомкнутом контуре? Встречались ли вам задачи на эту тему?

4. Почему и когда допустимо говорить о напряжении на катушке индуктивности несмотря на непотенциальный (вихревой) характер поля, действующего внутри катушки?

Литература

1. Задачи по физике: Уч. пособие. Под ред. Савченко О.Я. – М.: Наука, 1998.

2. Иродов И.Е. Основные законы электромагнетизма. – М.: Высшая школа, 1983 (и др. годы издания).

3. Яворский Б.М., Пинский А.А. Основы физики. В 2-х т. – М.: Наука, 1972.

4. Суорц Кл. Э. Необыкновенная физика обыкновенных явлений. т. 2. – М.: Наука, 1987.

5. Матвеев А.Н. Электричество и магнетизм. – М.: Высшая школа, 1983.

6. Гамов Г. Приключения мистера Томпкинса. – М.: Бюро Квантум, 1993.

_________________________

1Когда-то напряжённость и индукция вводились на основе различных эмпирических соображений. Но тогда и закон Архимеда представлялся фундаментальным фактом, – сейчас мы вполне понимаем его природу.

2Здесь сознательно допущено серьёзное упрощение: точные расчёты более громоздки, но приводят при сделанных приближениях к той же формуле (см., например, [5]).

3Здесь и везде все значения в единицах СИ, если нет специальных указаний. Размерность опускается.

4Мы приняли самую грубую оценку – для точечных тел. На семинаре можно учесть форму заряженных тел.

 5 Для строгих рассуждений изложенные представления недостаточны, нужно учитывать нарушение электронейтральности проводников из-за неодновременности входа электронов с одной стороны отрезка проводника и выхода – с противоположной.

6Когда-то эту формулу называли законом Ампера. Сейчас так называют теорему о циркуляции магнитного поля. Её изучение немного выходит за школьную программу.

7Можно посоветовать использовать приём Г.Гамова [6], допустив, что свет в аудитории распространяется со скоростью, например, 1 м/с. После этого положения релятивистской теории, включая процедуру синхронизации и создания местного времени в каждой точке, становятся наглядными, и вид преобразований координат и времени воспринимается совершенно естественно, даже без обращения к опытам Майкельсона.

8Объёмная плотность энергии по размерности (и по смыслу) совпадает с давлением.

Продолжение в № 24

.  .