Продолжение. См. № 17, 18, 19,
20/06
А.А.КНЯЗЕВ,
ЛПН, г. Саратов.
knf@sgu.ru
Олимпиадный материал в повседневной работе
преподавателя физики
Лекция 5. СТРОЕНИЕ ВЕЩЕСТВА В
ЗАДАЧАХ И ОЦЕНКАХ
1. Введение
Первые гипотезы о природе теплоты
появились только к концу XVII в., потому и вся
история этой части физических знаний короче, чем
история механики. А вот изучение этого раздела
ничуть не проще. Прежде всего потому, что
основные понятия, начиная, например, с количества
теплоты, полностью лишены наглядности. Кажется,
ясно, что имеется в виду, когда говорят о
температуре или о теплоте, а вот объяснить сможет
не каждый. Можно ли сообщать тепло, не изменяя
температуры? Что происходит, когда изменяется
температура, а что – когда сообщают тепло? Такие
вопросы поставил Джозеф Блэк (ок. 1760 г.), а затем
возникли и задачи: от оценки доли горячей воды
для приготовления ванны до вопросов современной
физики, химии, биофизики и технических расчётов.
Учителю известно, что по характеру
задач теория теплоты разделяется на два раздела:
статистическая (молекулярно-кинетическая)
теория и термодинамика. Однако в школьном курсе
столь чёткое деление отсутствует из-за
ограниченности школьной математики [1]. Кстати, в
школьной термодинамике не рассматриваются
вопросы, связанные, например, с анализом
скоростей химических реакций (химическая
кинетика), поэтому можно только недоумевать,
почему раздел называется «Термодинамика», а,
например, не «Термостатика».
2. Начальное знакомство
Можно провести некоторое
сопоставление знаний о теплоте с механикой. Так,
молекулярно-кинетической теории, направленной
на выяснение механизма тепловых явлений,
соответствует аппарат решения детальных
уравнений движения, а термодинамике
соответствует аппарат сравнения состояний
системы. Если опустить подробности, которые
стали острыми только к концу прошедшего века, то
сопоставление полное.
Практически первое знакомство с
тепловыми явлениями происходит в 7-м классе, ещё
до детального изучения механики. После
описательных представлений об основных тепловых
явлениях настаёт пора использования так
называемых уравнений теплового баланса. Эта
часть осваивается поначалу трудно (просто из-за
недостаточного ещё владения техникой решения
алгебраических уравнений), а затем, после
преодоления барьера, напоминает игру в
складывание кубиков.
В калориметр налили чашку горячей
воды, после чего его температура возросла на 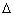 t1 = 5 °C.
После того как добавили ещё одну чашку,
температура возросла ещё на
t1 = 5 °C.
После того как добавили ещё одну чашку,
температура возросла ещё на 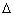 t2 = 3 °C. На сколько ещё
возрастёт температура, если добавить третью
чашку горячей воды? Теплообменом с окружающей
средой пренебречь. [ЗФТШ МФТИ, 1999/2000 уч.г.]
t2 = 3 °C. На сколько ещё
возрастёт температура, если добавить третью
чашку горячей воды? Теплообменом с окружающей
средой пренебречь. [ЗФТШ МФТИ, 1999/2000 уч.г.]
К решению. Основная трудность
этой задачи – стандартная для школы: нужно
ввести целую кучу величин, не упоминаемых в
условии, чтобы просто описать ситуацию, до поры
не обращая внимания на данные.
Итак, первая чашка наливается в
калориметр (термос):
C (t1 – t0) = cm(th
– t1),
где С – теплоёмкость калориметра,
t0 – его начальная температура, t1
– конечная температура смеси, c – удельная
теплоёмкость воды, m – её масса, th
– температура горячей воды. Очевидно, что t1
– t0 = 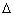 t1.
t1.
Вторая чашка в термосе:
C (t2 – t1) + cm(t2
– t1) = cm(th – t2).
Третья чашка:
C (tх – t2) + 2cm(tх
– t2) = cm(th – tх).
Введя обозначение tх – t2
= Х и повозившись немного с системой
уравнений, получаем Х = 2 °C.
Итак, восемь неизвестных при шести
уравнениях! Главное – не отчаиваться сразу, ведь
отыскивать все эти неизвестные не требуется!
При некоторых условиях чистую воду
без примесей можно охладить до температуры –5 °C,
и она не замерзнёт. Если после этого какой-либо
предмет, например, песчинка, попадёт в
переохлаждённую воду, то мгновенно начинается
процесс кристаллизации. Вся ли вода замёрзнет
при этом? Какая часть воды замёрзнет?
К решению. Охлаждая воду, мы
отняли некоторое количество теплоты Q = cm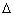 t. Этого
хватило бы на кристаллизацию определённой массы
льда:
t. Этого
хватило бы на кристаллизацию определённой массы
льда: 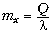 , но сначала
этого почему-то не произошло. Теперь именно эта
масса и замерзнёт – за счёт отнятой теплоты:
, но сначала
этого почему-то не произошло. Теперь именно эта
масса и замерзнёт – за счёт отнятой теплоты: 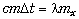 , отсюда
, отсюда
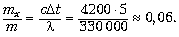
Таким образом, замёрзнет только 6% всей
массы воды. Вода лишь подёрнется льдом, а не
превратится в ледяной ком, как может нарисовать
воображение, всё-таки удельная теплота
агрегатного перехода 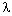 ~ 106 Дж/кг и «удельная теплота
охлаждения» (назовём эту величину так) c
~ 106 Дж/кг и «удельная теплота
охлаждения» (назовём эту величину так) c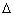 t ~ 104
Дж/кг различаются здесь более чем на порядок.
t ~ 104
Дж/кг различаются здесь более чем на порядок.
3. Связь с механическими
представлениями
И всё-таки способность вникнуть в суть
решаемых задач усиливается именно после
освоения механики и сопоставления её с
положениями молекулярно-кинетической теории.
Без знания механики как азбуки физики невозможно
понять глубину и красоту природы.
К решению. Школьники имеют
представление о характере действия
межмолекулярных сил, но редко представляют
количественную сторону, важную для понимания
механизма их проявления. Теплота испарения r
есть, по сути, работа против сил взаимодействия
молекул F, совершаемая при отрыве их друг от
друга за счёт кинетической энергии: r ~ FRN,
где R – межмолекулярное расстояние ~ 10–10 м,
а N – число оторванных молекул. Число
молекул в единице массы (1 кг) может быть оценено
как 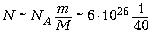 ~ 1025
штук (для молярной массы взято значение из
середины таблицы элементов ~40 г/моль).
~ 1025
штук (для молярной массы взято значение из
середины таблицы элементов ~40 г/моль).
Собирая все данные, получаем для
значения силы F ~ 10–9 Н. С такими силами
имеют дело в современных атомно-силовых
микроскопах.
4. Термодинамические величины
Обязательно обратите внимание
учеников на то, что для любого числа молекул
(атомов) вполне можно записать систему уравнений
движения. Вот только решение (если даже провести
его через суперкомпьютер) окажется бесполезным:
траектория отдельного атома перестаёт быть
представительной характеристикой – все похожи
друг на друга. Теперь важны другие величины,
ненужные для одной молекулы, но описывающие
поведение ансамбля.
Вот, вкратце, о некоторых из них:
Температура – доля кинетической
энергии хаотического поступательного движения
молекул, приходящаяся на одну молекулу ансамбля.
Ввиду малости для макромира измеряется в особых
единицах (градусах абсолютной шкалы) через
пересчётный коэффициент k ~ 10–23
Дж/град:
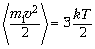 ,
,
где m1 – масса молекулы.
Из этого соотношения полезно выделить
среднюю квадратичную скорость хаотического
(теплового) движения 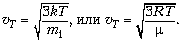 Формула показывает, что при
выравнивании температур контактирующих тел
тепловые скорости хаотического движения атомов,
молекул, кластеров, наноструктур, коллоидов,
пылинок, вирусов оказываются различными.
Формула показывает, что при
выравнивании температур контактирующих тел
тепловые скорости хаотического движения атомов,
молекул, кластеров, наноструктур, коллоидов,
пылинок, вирусов оказываются различными.
Давление – средняя сила ударов,
рассчитанная на единицу площади поверхности,
ограничивающей движение молекул. Используя
теорему об изменении импульса и элементарные
представления об усреднении, обычно получают
связь p = nkT, где n – концентрация;
Объём – предоставленный для
движения всему рассматриваемому ансамблю
молекул. Может существенно отличаться от
суммарного собственного объёма молекул (см.,
например, задачу в лекции 1).
Внутренняя энергия – для
идеальных одноатомных газов, рассчитывается
как сумма всех кинетических энергий молекул 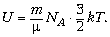 Для
взаимодействующих ансамблей – это полная
кинетическая энергия и энергия всех
взаимодействий внутри ансамбля молекул.
Исключается лишь макроскопическая энергия
(«внешняя») данного ансамбля как целого.
Для
взаимодействующих ансамблей – это полная
кинетическая энергия и энергия всех
взаимодействий внутри ансамбля молекул.
Исключается лишь макроскопическая энергия
(«внешняя») данного ансамбля как целого.
Количество теплоты – работа,
совершаемая диссипативными (необратимыми)
межатомными силами при беспорядочном (тепловом)
движении . Результат совершения работы
микроскопического уровня может проявляться на
макроуровне как повышение температуры,
излучение или агрегатный переход. И, наоборот,
макроскопическая работа, затрагивающая
деформацию системы, продолжается далее
межатомным движением – возникновением
некоторого количества теплоты и изменением
кинетической энергии молекул, т.е. изменением
температуры и излучением. Понимание этого важно,
например, для следующей ситуации: несмотря на то,
что в системе планета–маятник все силы
внутренние, т.е. скомпенсированные, качания
маятника прекращаются со временем, т.е.
кинетическая энергия системы изменяется. Это
потому, что есть силы, совершающие ненулевую
работу.
Такая программа удобна и важна для
учителя, поскольку позволяет избежать
недоговорённостей и передачи в поколения,
например, такой устаревшей терминологии, как
«поглощение теплоты». Являясь разновидностью
работы, теплота не поглощается, не накапливается.
Теплота совершается, передаётся, отнимается,
наконец, возникает. И хотя, например, при
изохорном процессе накапливание всё-таки можно
оправдать, лучше избегать этого, поскольку нужны
оговорки, связанные с определением функций
состояния (говорить о накапливании можно только
тогда, когда разность значений не зависит от
траектории процесса).
Не останавливаясь на других известных
положениях, скажу, что для начала вполне можно
опустить подробности статистических приёмов [2].
Зато важно «потрогать руками» каждую из
введённых величин, постепенно, по мере изучения,
через задачи-оценки.
К решению. Запишем закон
изменения импульса р ансамбля
молекул, летающих над дном сосуда, за время 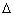 t. Большинство
молекул (атомов) находится в полёте, сталкиваясь
друг с другом. Силы их взаимодействия –
внутренние, они не входят в запись. Но есть и две
внешние силы: некоторые из молекул время от
времени ударяют в дно, – в это время на них
действуют силы нормальной реакции Nj;
кроме того, на все без исключения молекулы
действует внешняя сила тяжести mgi.
t. Большинство
молекул (атомов) находится в полёте, сталкиваясь
друг с другом. Силы их взаимодействия –
внутренние, они не входят в запись. Но есть и две
внешние силы: некоторые из молекул время от
времени ударяют в дно, – в это время на них
действуют силы нормальной реакции Nj;
кроме того, на все без исключения молекулы
действует внешняя сила тяжести mgi.
Итак, в проекции на вертикальную ось:
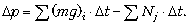
В итоге центр масс газа остаётся на
месте, т.e. 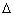 p
= 0. Получаем
p
= 0. Получаем 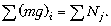 Отсюда, вычисляя левую сумму
Отсюда, вычисляя левую сумму 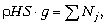 или, окончательно p =
или, окончательно p = 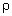 gH. Здесь
gH. Здесь 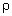 – плотность газа.
– плотность газа.
Так снимается недоумение: почему в
создании давления участвуют и те молекулы,
которые не ударяли о дно сосуда? Суммарные толчки
(импульс силы) в дно подлетевших молекул при
ударах таковы, что позволяют поддержать
хаотическое движение и удержать от падения на
дно все остальные молекулы.
5. Уравнения состояния
Предыдущая формула для давления газа
была получена по той же схеме, что и теорема об
изменении импульса, – путём суммирования в
системе уравнений движения, записанных для всех
молекул газа. Если избрать другую технологию,
подобную той, что используется при получении
теоремы об изменении кинетической энергии (см.
мою статью в «Физике» № 37/04), то затем, путём
усреднения [3], можно получить уравнение
состояния, имеющее вид:
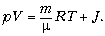
Кроме хорошо известных в школьном
курсе физических величин, здесь записано
слагаемое J, соответствующее усреднённой
энергии сил взаимодействия молекул (атомов). Для
случая идеального газа вкладом этого слагаемого
можно пренебречь, и тогда теоретически
полученное уравнение совпадает с обобщённым
уравнением состояния
pV = 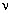 RT,
или
RT,
или 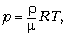 или p = nkT.
или p = nkT.
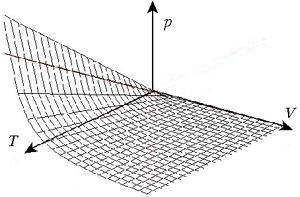
Не часто в школьных курсах явно
говорится, что уравнение состояния описывает
поведение трёхмерной функции p(V, T),
так что можно отдельно изучать её различные
сечения, отвечающие простейшим (элементарным)
газовым процессам: изобарному, изохорному,
изотермическому. Важно понимать, что уравнение
состояния не описывает никаких процессов, оно
всегда одно и то же. А процессы описываются
дополнительным уравнением, когда состояние газа
изображается точкой, движущейся в пространстве p,
V, T. Ну хотя бы по закону pV = 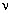 RT0.
Впрочем, масса газа тоже может изменяться. Задач
на эту тему много, но все они достаточно просты,
пока не связаны с энергетикой.
RT0.
Впрочем, масса газа тоже может изменяться. Задач
на эту тему много, но все они достаточно просты,
пока не связаны с энергетикой.
Шаровая молния представляет собой
слабо светящийся газовый шар, свободно плавающий
в воздухе. По одной из моделей, газ внутри
является комплексным соединением, каждая
частичка которого (кластер) представляет собой
ион азота, связанный с несколькими молекулами
воды. Потерянные азотом электроны связаны водой,
и кластер в целом нейтрален. Определите, сколько
молекул воды связывает кластер, если температура
внутри составляет 600 °С, а снаружи 20 °С. [№ 9.148 из
сборника «3800 задач по физике».]
К решению. Сравним уравнения
состояния для воздуха снаружи и для газа внутри
шаровой молнии:
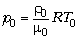 – для
воздуха;
– для
воздуха;
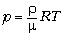 – для
вещества молнии.
– для
вещества молнии.
Дополнительно известно, что p = p0,
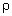 =
= 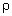 0 и
0 и 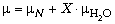 . Продолжив сравнение с учётом данных
задачи, получаем X = 4.
. Продолжив сравнение с учётом данных
задачи, получаем X = 4.
Что касается описания поведения
жидкостей и твёрдых тел, то расчёт энергии сил
взаимодействия здесь очень сложен. Этому есть по
меньшей мере две причины: 1) в таких веществах, как
металлы и сплавы, а также в ионных или атомных
кристаллах молекул как таковых не существует, –
моделью вещества здесь является плазма твёрдого
тела; 2) взаимодействие атомов на расстояниях
порядка размеров самих атомов не описывается
теорией Ньютона, поэтому исходные уравнения
движения должны быть заменены уравнениями
квантовой теории микромира. Да и характеристики,
описывающие свойства тел и происходящие в них
процессы, тоже изменяются. Такими величинами
являются, как известно, теплоёмкость, вязкость,
теплопроводность, коэффициенты взаимной
диффузии, удельное сопротивление и т.д.,
связанные между собой известными соотношениями
[2, 3].
Иное дело – так называемые реальные
газы, когда молекулы вещества сохраняют признаки
поведения в газах, но уже не свободны от влияния
межатомных сил притяжения из-за малой
кинетической энергии, сравнимой с потенциальной
энергией взаимодействия. Расчёт второго
слагаемого остаётся сложным, однако известно
несколько вариантов удовлетворительного
описания уравнения состояния.
Приведём два примера:
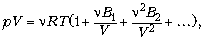 где Вi
– вириальные (силовые) коэффициенты
(Камерлинг-Оннес, 1901 г.);
где Вi
– вириальные (силовые) коэффициенты
(Камерлинг-Оннес, 1901 г.);
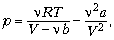 где a
и b – постоянные (Ван дер Ваальс, 1873 г.).
где a
и b – постоянные (Ван дер Ваальс, 1873 г.).
Изотерма газа Ван дер Ваальса ниже
некоторого (критического) значения температуры
уходит вниз и приобретает причудливый вид кривой
третьего порядка (см. рисунок). Такой газ,
охлаждённый ниже критической температуры,
называется уже паром (он обладает способностью к
конденсации). Приближённость описания поведения
пара видна уже из того, что экспериментальные
изотермы отличаются от теоретических: на рисунке
область нарушения отмечена утолщённой линией, а
участки реальных изотерм в этой области – прямые
линии (диаграммы Эндрюса).
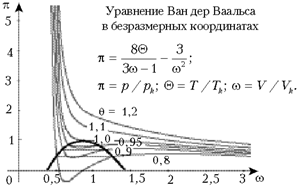
В школе обсуждается в основном
идеальный газ, а знакомство со свойствами
реального газа ограничивается темой
«Влажность». Однако и для этой темы знание
внешнего вида реальных изотерм полезно и
помогает ориентироваться в ситуации.
К решению. Взаимодействие молекул
сдерживает силу ударов о поверхность.
Представим, что все эти молекулы представляют
теперь идеальный газ, и рассчитаем давление: 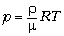 ~108 Па, т.е.
давление возросло бы более чем в десять тысяч раз
по сравнению с давлением воды на дно стакана.
~108 Па, т.е.
давление возросло бы более чем в десять тысяч раз
по сравнению с давлением воды на дно стакана.
6. Первое начало термодинамики
С учётом сказанного выше здесь
наблюдается следующая аналогия. Если для
макросистемы закон превращения механической
энергии может быть получен теоретически и
записывается как 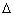 Е =Адис, то с учётом
микроскопического строения вещества его можно
записать:
Е =Адис, то с учётом
микроскопического строения вещества его можно
записать:
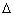 Емакроскоп
+
Емакроскоп
+ 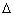 Uмикроскоп
= Адис.макроскоп + Qмикроскоп.
Uмикроскоп
= Адис.макроскоп + Qмикроскоп.
Это и есть соотношение, к которому
термодинамика пришла независимо от механики, по
сути, эмпирическим путём. Если изменения
макроскопической энергии не происходит, то
запись может иметь вид:
Qмикроскоп = 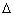 Uмикроскоп + Асистемы
макроскоп.
Uмикроскоп + Асистемы
макроскоп.
В последней записи допущены
общепринятые, но не имеющие особой важности
нюансы: вместо работы внешних диссипативных сил
над системой введена работа системы против этих
сил, а слагаемые в записи изменили свои места. В
дальнейшем будем следовать именно этой записи,
опуская пояснительные индексы: Q = 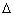 U + А.
U + А.
Для предупреждения недоразумений
напомним, что величина 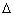 Е представляет сумму изменения
макроскопической кинетической энергии системы и
взятой с обратным знаком работы консервативных
сил (разность потенциальных энергий
макросистемы). Иными словами, Е = K + U.
Тогда работа диссипативных сил остаётся в правой
части равенства, выражающего, по сути, теорему о
кинетической энергии. Это очень тонкий момент,
выяснение которого отложим до лекции об
электродинамических силах взаимодействия
атомов, однако логика здесь именно такая, и
попытка упростить её только запутывает дело.
Именно это опрощение и недосказанность
доминируют сейчас в учебниках.
Е представляет сумму изменения
макроскопической кинетической энергии системы и
взятой с обратным знаком работы консервативных
сил (разность потенциальных энергий
макросистемы). Иными словами, Е = K + U.
Тогда работа диссипативных сил остаётся в правой
части равенства, выражающего, по сути, теорему о
кинетической энергии. Это очень тонкий момент,
выяснение которого отложим до лекции об
электродинамических силах взаимодействия
атомов, однако логика здесь именно такая, и
попытка упростить её только запутывает дело.
Именно это опрощение и недосказанность
доминируют сейчас в учебниках.
Вот, собственно, и вся идеология
термодинамики в части, затрагивающей первое
начало. Дальше следует технология расчётов.
Например, для идеального газа: 
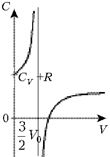
Расчёт теплоёмкости возможен на
основе следующей схемы рассуждений: 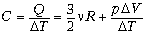 .
.
Ответ. с = 3,5R. На графике
приведён ход зависимости теплоёмкости от объёма
для всего процесса. Видно, что значение
теплоёмкости на определённых участках процесса
может быть даже отрицательным. 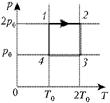
На каком участке цикла, изображённого
на плоскости р, T, работа газа
наибольшая по абсолютной величине?
Ответ. На участке 2-3. Важно не
только перечертить график в координатах р, V,
но и учесть указанные значения параметров.
7. О втором начале
Вообще говоря, в этой теме
рассматриваются вопросы действия тепловых машин
и особенностей поведения ансамбля многих частиц
– утверждается, что явления, развивающиеся без
внешнего воздействия, никогда не проходят через
предшествующие точки. Однако, если первая часть
иллюстрируется в школе решением задач, то вопрос
об энтропии практически даже не упоминается в
большей части учебников и программ [1]. 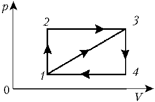
К решению. Задача относится к
числу стандартных, однако для решения нужно
чётко контролировать ситуацию. Известно, что кпд
любого механизма или машины определяется по
соглашению. Так, если для механизмов принято
определять КПД как отношение работы, которую мы
объявили полезной, к работе всех внешних сил, то
для тепловых машин – это отношение работы сил по
расширению рабочего тела к количеству теплоты,
полученному от источника. 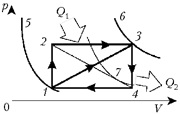
Вообще изображение цикла машины на
графике р, V очень удобно, поскольку
позволяет оценить значение работы как площади
цикла в соответствующем масштабе единиц. Но вот
процедура непосредственного графического
расчёта количества теплоты здесь довольно
замысловата, хотя и возможна (см., например,
задачу Всероссийской олимпиады в Ульяновске, 1999
г.). При этом важно определить, в каких процессах
теплота сообщается, а в каких – отбирается.
Удобно следовать следующему простому правилу:
нужно ограничить цикл двумя адиабатами – 5 и
6 – они определяют «русло» потока тепла Q1
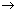 Q2.
При этом разность значений входящего количества
теплоты Q1 и выходящего Q2 –
и есть работа цикла. В нашем случае для первого
цикла тепло поступает в процессе 1-3, а
во втором – в процессах 1-2 и 2-3. При этом
(Q12 + Q23) – Q13 = A1231,
причём A1231 = A1341.
Q2.
При этом разность значений входящего количества
теплоты Q1 и выходящего Q2 –
и есть работа цикла. В нашем случае для первого
цикла тепло поступает в процессе 1-3, а
во втором – в процессах 1-2 и 2-3. При этом
(Q12 + Q23) – Q13 = A1231,
причём A1231 = A1341.
С учётом сказанного запишем:
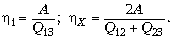
Получим 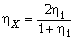 .
.
Задача усложнится, если понадобится
определить КПД цикла 1-2-4-1. Теперь адиабата 6
сменится адиабатой 7, и точка смены знака
количества теплоты ляжет на диагональ 2-4.
Тогда для решения понадобятся дополнительные
данные о виде очертания цикла (см., например,
задачу зональной олимпиады в Ростове-на-Дону, 1999
г.).
8. Заключение
Ограничение на объём не даёт
возможности затронуть одновременно и
особенности идеологического характера при
изучении темы, и приложения этой идеологии к
вопросам конкретного решения задач. Основной
объём материала посвящён обсуждению смысла
известных соотношений и связей между другими
разделами, поскольку без этих знаний
затрудняется анализ физических ситуаций. За
пределами остались, например, явления переноса,
одно время исчезнувшие из практики олимпиад, а
теперь появившиеся снова. Учителю, хотя бы для
факультативного варианта, стоит разработать
темы явления теплопроводности и вязкого трения.
Они совершенно естественно следуют за темами
термодинамики, объясняя такие реальные явления
как, например, полёт капли дождя (пули) в воздухе с
учётом сопротивления среды. Интересен и процесс
реальной передачи тепла, когда в отличие от
ситуаций с медленным нагреванием одна часть
вещества имеет одну температуру, а другая часть
– уже другую (см., например, задачи для 9-го класса
всероссийской олимпиады-2002/03 в Воронеже).
Отметим, что разбор интереснейших
задач представлен большим количеством
превосходных тематических статей,
опубликованных в разные годы, например, в журнале
«Квант». Довольно много примеров можно найти и в
постоянно функционирующем разделе газеты
«Физика», посвящённом анализу задач экзаменов и
олимпиад.
Вопросы для самоконтроля
1. Почему в тепловых расчётах важную
роль отводят не средней скорости хаотического
движения молекул, а именно среднеквадратичной?
2. Может ли температура системы
оставаться постоянной, если ей передаётся или у
неё отбирается тепло?
3. Попробуйте подобрать вириальные
коэффициенты в уравнении Камерлинг-Оннеса так,
чтобы график изотермы оказался близким к
изотерме реального газа.
4. Что происходит с газом на участке
процесса, где теплоёмкость отрицательная?
Литература
1. Захаров Д.М. Совершенствовать
физико-математическое образование. – Физика
(«ПС»), № 10/05.
2. Иродов И.Е. Физика макросистем.
Основные законы. – М.– С.Пб.: Физматлит, 2001.
3. Матвеев А.Н. Молекулярная физика. – М.:
Высшая школа, 1981.
Продолжение в № 22