|
Продолжение. См. № 17/06
А.А.КНЯЗЕВ,
ЛПН, г. Саратов
knf@sgu.ru
Олимпиадный материал в
повседневной работе преподавателя физики
Лекция 2. МЕХАНИКА – ВЗГЛЯД НА
ИЗЛОЖЕНИЕ МАТЕРИАЛА. КИНЕМАТИКА
Профессор В.Л.Кирпичёв в книге «Беседы
о механике» [1], ставшей сейчас раритетом,
приводил доводы в пользу такого порядка изучения
механики, при котором после кинематики идёт
вначале статика, и уже затем, как более сложная, –
динамика. Такой путь удобен и с позиции
следования историческому развитию физики, и с
позиции логики. Есть, однако, и иные мнения.
Исторический путь интересен и важен, однако в
действительности настолько запутан, что редкий
университет отваживается сейчас иметь курс
истории науки, и то лишь на старших курсах. А без
него теряется гуманитарная составляющая науки и
культивируются технократические позиции.
Современный же взгляд на динамику привлекает
изначальной классификацией взаимодействий с
последующим логическим развитием взглядов. И
тогда статика отходит на второй план. Правда, на
выработку такого взгляда ушло более двадцати
веков! Изначально же любой человек
придерживается «здравого смысла», изложенного
Аристотелем. Начав с классификации
взаимодействий, учитель рискует тем, что ученик
со слабой ещё склонностью к философии разовьёт в
себе двойной стандарт: в ответах по теории –
взаимодействия и законы Ньютона, а в жизни –
аристотелевские взгляды и беспомощность при
решении задачи. Скажу сразу: в младших классах
мне удаётся лавировать, не прибиваясь ни к одной
из линий. Думаю, что на раннем этапе гораздо
важнее развить элементарный аппарат описания
явлений как основу для дальнейших предметных (не
пустопорожних!) разговоров, чем излагать
концепцию науки и заучивать определения. Так,
значение ускорения свободного падения можно
вначале декларировать как опытный факт,
например, вместе с комфортным ускорением на
железной дороге (0,2 м/c2). Затем, говоря о
силах, ввести закон тяготения и напряжённость
взаимодействия, отметив попутно совпадение
обозначений. И только в динамике, решая задачу о
свободном падении, снова возвратиться к теме
ускорения – без обращения к эйнштейновской
эквивалентности. Вообще говоря, усложнять проще,
чем упрощать, – дети и без вас делают это с
фантастической виртуозностью. Каждому учителю
искренне хочется сразу делать множество
оговорок, уточнений (а с возрастом это становится
просто бедствием). Важно сдерживать себя –
подробности нужны для жизни далеко не всем и
более уместны на факультативном занятии. Но вот
если вас всё-таки «достали» вопросами, долг
учителя соблюсти золотую середину, не
отмахнуться, не оттолкнуть от себя и потерять
авторитет, но и не растекаться «мыслью по древу»*.
(* Кстати, есть мнение учёных-филологов, что
правильное выражение «растекаться мысью по
древу» происходит от древнеславянского мысь, что
значит белка. А слово мысль появилось
при многократном переписывании «Слова о полку
Игореве». – Ред.)
Нужно закончить ответ раньше, чем
детям станет скучно. Здесь-то и нужна эрудиция,
запас профессиональных знаний, многократно
превышающий диапазон вопросов, и, конечно,
определённый артистизм.
С любой из упомянутых позиций
несомненно одно: вначале необходимо освоить
математический аппарат механики – кинематику.
Равномерное прямолинейное
движение
Главная цель учителя на первом этапе
детального знакомства с физикой после обзора
явлений в
7-м классе – всё-таки не физика как наука о
Природе, а завоевание математики. Дети могут
решать довольно изощрённые задачи
математического содержания, а для физики нужно
совсем мало – искусство записи и решения систем
уравнений, сначала линейных, затем квадратных. И
конечно, математическая графика. Но всю эту
программу учитель должен сделать сам.
Без преувеличения, важное препятствие,
с которым приходится встречаться (после неумения
считать!), – боязнь введения обозначений величин,
значения которых не заданы в условии задачи.
Гидрофон, установленный вблизи дна,
зарегистрировал последовательность сигналов,
связанных с подводным взрывом на дне. Между
первым и вторым сигналами прошла 1 с, между первым
и третьим – 3 с. Определите расстояние до точки
взрыва, приняв скорость звука в воде равной 1500
м/с.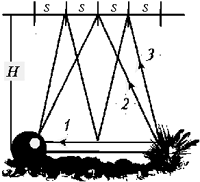
К решению. Что такое гидрофон,
нужно объяснить ещё при чтении задачи
(современные дети лучше знают, что такое
«матрица» и «покемон», чем эхолот и гидролокатор;
родители – тоже). Затем вместе выясним, при чём
здесь второй и третий сигналы. А дальше и
начинается проблема обозначений и записи
условия, поскольку нужно преодолеть смущение при
введении глубины водоёма, о которой в условии
ничего не сказано.
Запишем два уравнения:
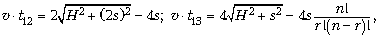
решая которые, получаем 4s = 3,75 км.
Эта проблема тянет за собой медленное
освоение умения выделить главную модель явления.
Мешает и ошибочно понимаемая школьниками
стандартизация обозначений величин на уроках
физики и математики. Школьники, освоившие
способы решения линейного или даже квадратного
уравнения на уроках математики, оказываются при
этом не в состоянии «узнать» его в формулах
кинематических законов, где роль «икса» берёт на
себя время. Такой «перекос» в сторону математики
понятен: занятия математикой начинаются с первых
школьных шагов, и даже раньше. Как ни
парадоксально, но, пожалуй, изучение физики
требует при анализе конкретной ситуации навыков
более значительного абстрагирования, чем при
решении математических задач. Школьная
математика в основном алгоритмизована и поэтому
гарантирует успех. Даже если не достаточно ясен
смысл понятий, школьник вполне может производить
стандартные операции и даже проявлять
определённую изобретательность в
преобразованиях. Может быть, именно посредством
этого примерно к 8-му классу мозг школьника и
подготавливается к восприятию физики. Впрочем,
выработке навыков абстрагирования не меньше
способствуют и занятия поэзией, музыкой и просто
наработка жизненного опыта. И всё же поначалу
школьнику очень сложно научиться воспринимать
реальный зелёный с четырьмя колёсами автомобиль
как материальную точку, не испытывающую подчас
даже сопротивления воздуха. А без навыков
абстрагирования и создания модели в физике не
решишь даже простую задачку. Да ещё вокруг, как
мухи, летают услышанные где-то слова о силах
сопротивления, центробежных силах, о зависимости
массы от скорости, и ещё, и ещё... Вот здесь-то и
выходит на первый план тезис о важности именно
описания явления, а не разговоров о нём1 .
Вот почему так важно «завоевание математики» –
физики будет ещё много.
Успех освоения понятий кинематики, по
мнению автора, во многом зависит от того, как
скоро удастся ознакомить школьника с
координатным способом описания движения, решая
сначала одномерные задачи, а затем и
пространственные. Не стану приводить примеры
таких задач – они многочисленны, начиная с
задачников Рымкевичей.
Можно, наверное, согласиться с тем, что
координатный метод в физике, равно как метод
составления уравнений в математике, быстрее и
надежнее приводит к получению результата, чем
способ поэтапных рассуждений, которым в школе
увлекались в начале прошлого уже века. Правда,
некоторые ученики долгое время цепляются за
непосредственные вычисления, без составления
уравнений в координатах. И ведь ухитряются
решать! Думаю, что учителю не нужно увлекаться
эвристическими решениями, несмотря на ценность
уникального мышления для генерации идей.
Приходится убеждать в малой эффективности
самобытных рассуждений при анализе явлений,
описываемых нелинейными функциями, подбирая
соответствующие задачи.
Катер идёт по реке, имея собственную
скорость 18 км/ч, тогда как скорость течения реки
2 м/с. Сколько времени займёт поездка туда и
обратно в населённый пункт, отстоящий на 100 км от
исходного? Изменилось бы это время, если бы
скорость течения стала равной 3 м/c?
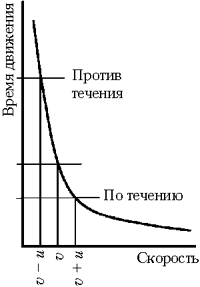
К решению. Класс разделяется на
«Тупоконечников» и «Остроконечников»: одни
утверждают, что потери времени при движении
против течения компенсируются его экономией при
движении по течению, другие с недоумением
представляют свои расчёты:
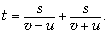
Комментируя решение, обратите
внимание на свойства несимметричного поведения
нелинейной функции в окрестности произвольной
точки, а также на то, что при u >  катер вообще не может
подняться против течения (на горной реке не
поможет даже водный мотоцикл). катер вообще не может
подняться против течения (на горной реке не
поможет даже водный мотоцикл).
По дороге движется колонна
автомобилей, соблюдая дистанцию. Инспектор ГИБДД
заметил, что, если он едет со скоростью 36 км/ч, то
каждые 10 с его обгоняет автомобиль колонны. Если
же он увеличивает свою скорость до 90 км/ч, то он
сам обгоняет автомобили каждые 20 с. С каким
интервалом будут проходить автомобили мимо
инспектора, если он остановится? (Олимпиада МОиН
2005 г., 8-й класс.)
К решению. Нужно просто два раза
решить задачу о том, как нагоняют друг друга два
автомобиля на прямой дороге, выезжая из двух
разных пунктов. А если использовать метод
поэтапных рассуждений, то легко запутаться. Ответ.
5 с.
С какой скоростью нужно бросить
вертикально вверх камень, чтобы его перемещение
за четвёртую секунду составило s = 1 м? (6-я
Соросовская олимпиада школьников, 1999/2000 уч.г., 1-й
тур.)
К решению. Здесь нужно чётко
ответить на вопрос, записав функцию модуля. Иначе
можно упустить второе решение:
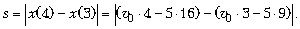
Ответ.  0 = 36 м/с (или 34 м/с). 0 = 36 м/с (или 34 м/с).
Вверх по узкой неизвестной реке
уходит катер с экспедицией. Каждый час штурман
опускает в реку пластиковый баллон с донесением
для базового лагеря. С какой частотой будут
принимать донесения на базе, если скорость
катера относительно берега постоянна и равна  = 20 км/ч, а скорость
течения u = 1 м/с? = 20 км/ч, а скорость
течения u = 1 м/с?
К решению. Задача имеет варианты,
но, по сути, она об известном эффекте Доплера (1842
г.), широко используемом в технике и диагностике.
Пластиковые баллоны играют роль периодических
сигналов, посылаемых источником с частотой F0
= 1 раз/ч, скорость течения есть скорость
распространения сигнала в среде,  – скорость источника
относительно среды. Если не увлекаться пустыми
рассуждениями и считать, что баллон, брошенный в
воду, тут же приобретает скорость течения, то
школьники получают решение: – скорость источника
относительно среды. Если не увлекаться пустыми
рассуждениями и считать, что баллон, брошенный в
воду, тут же приобретает скорость течения, то
школьники получают решение:
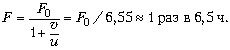
Кинематика в пространстве
Раннее освоение метода координат
помогает простому переносу закономерностей
одномерного движения на двух- и трёхмерное.
В точке М в углу, на полу пустого
хранилища прямоугольной формы размером 4 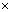 8 м, сидит в своей
норке мышонок, а из точки K, на середине
короткой стороны, за ним следит котёнок. В
некоторый момент они одновременно начинают
бежать. Графики составляющих скоростей показаны
на рисунке. Сумеет ли котёнок перехватить
мышонка за указанное на рисунке время? На сколько
короче путь котёнка? Ось Х – короткая
сторона пола амбара, ось Y – длинная. 8 м, сидит в своей
норке мышонок, а из точки K, на середине
короткой стороны, за ним следит котёнок. В
некоторый момент они одновременно начинают
бежать. Графики составляющих скоростей показаны
на рисунке. Сумеет ли котёнок перехватить
мышонка за указанное на рисунке время? На сколько
короче путь котёнка? Ось Х – короткая
сторона пола амбара, ось Y – длинная.
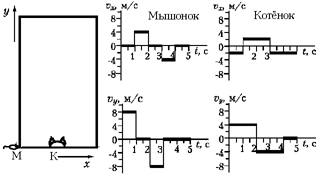 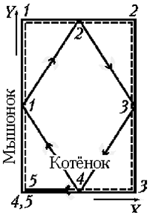
К решению. Видно, что мышонок
быстро, за 4 с, обегает периметр амбара 24 м и
скрывается в норке на секунду раньше, чем к ней
подбегает котёнок, пытавшийся перехватить
мышонка диагональными рывками на пути длиной 18 м.
Средняя скорость мышонка 6 м/с, котёнка – 4,5 м/с.
(Аналогичные задачи описаны, например, в журнале
«Квант» № 6, 1979.)
«Зажигают» ребят и задачи на
трёхмерное движение.
Через открытое окно в комнату влетел
жук. Расстояние от жука до потолка изменялось со
скоростью 1 м/c, расстояние до стены,
противоположной окну, менялось со скоростью 2 м/c,
до боковой стены – со скоростью 2 м/c. Через 1 с
полёта жук попал в угол между потолком и боковой
стеной комнаты. Определите скорость полёта жука
и место в окне, через которое он влетел в комнату.
Высота комнаты 2,5 м, ширина 4 м, длина 4 м. (Задача из
сборника под ред. О.Я.Савченко.)
Ответ.  = 3 м/c, 1 м от потолка и 2 м от боковой стены.
При обсуждении можно даже получить теорему
Пифагора в обобщённом трёхмерном варианте: x2
+ y2 + z2 = L2. = 3 м/c, 1 м от потолка и 2 м от боковой стены.
При обсуждении можно даже получить теорему
Пифагора в обобщённом трёхмерном варианте: x2
+ y2 + z2 = L2.
Равнопеременное движение
Одновременно с введением понятия
координаты на прямой при введении скорости и
ускорения одномерного движения не следует долго
задерживаться на обсуждении равномерного
движения или линейного изменения какой-либо
величины. Переход к движению с ускорением
начинаем с усложнения закона изменения скорости
– от постоянного значения к линейному изменению
со временем. Затем определяем закон изменения
координаты – по площади под графиком скорости
(как, например, в учебниках А.В.Пёрышкина). И
теперь подходит пора отметить важнейшую
структуру записи кинематических законов
движения. Её суть в том, что для описания любого
(даже более сложного, чем равнопеременное!)
движения необходимы два соотношения –
зависимость скорости от времени и зависимость
координаты от времени. Для пространственного
движения соответствующие зависимости
необходимо записать для каждой координаты. В
дальнейшем, при решении задач, делайте акцент на
наличие непременно двух кинематических
соотношений – для скорости и для координаты.
Конечно, встречаются простые вопросы, для ответа
на которые достаточно только одного соотношения.
Сделав такое превентивное замечание, вы, по сути,
выходите на ньютоновскую идеологию решения
дифференциального уравнения движения 2-го
порядка (подробности в следующей лекции).
Возможно, вы и не будете учить этому своих
учеников, но «рука поставлена верно».
Важно предупредить возможные ошибки
записи кинематических соотношений равномерного
и в особенности равнопеременного движения.
Школьники (и даже учителя) иногда полагают, что
знак при ускорении определяется характером
процесса – ускоренное движение или замедленное.
Так, рассматривая задачу о полёте мяча вверх,
некоторые пытаются искусственно разделить этот
процесс на полёт вверх (равнозамедленный) и
падение вниз (равноускоренное). Необходимо
показать, что кинематические соотношения
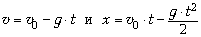
описывают сразу обе ветви этого
движения (пока  0
> gt – движение вверх, а по прошествии
времени, когда 0
> gt – движение вверх, а по прошествии
времени, когда  0
< gt, – движение вниз, поскольку скорость
изменяет знак), а знаки при слагаемых
определяются исключительно выбором
положительного направления осей системы отсчёта
и ориентации относительно этих осей направлений
скорости и ускорения. В приведённой выше записи
был выбран первый вариант ориентации оси X.
Вообще удобнее не пользоваться терминами
«равнозамедленное» и «равноускоренное» при
наличии термина «равнопеременное движение»,
хотя упомянуть о существовании этих
анахронизмов необходимо обязательно,
предупреждая возможные неточности в тестах и в
различных житейских ситуациях. 0
< gt, – движение вниз, поскольку скорость
изменяет знак), а знаки при слагаемых
определяются исключительно выбором
положительного направления осей системы отсчёта
и ориентации относительно этих осей направлений
скорости и ускорения. В приведённой выше записи
был выбран первый вариант ориентации оси X.
Вообще удобнее не пользоваться терминами
«равнозамедленное» и «равноускоренное» при
наличии термина «равнопеременное движение»,
хотя упомянуть о существовании этих
анахронизмов необходимо обязательно,
предупреждая возможные неточности в тестах и в
различных житейских ситуациях.
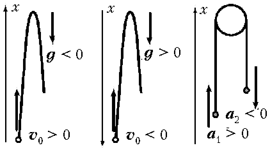
Камень движется первую половину пути
замедленно, а вторую – ускоренно. Означает ли
это, что в первом случае его ускорение
отрицательно, а во втором – положительно? – этот
вопрос образно закрепляет сказанное в сознании и
навсегда отсекает дальнейшие ошибки.
Вот две задачи, демонстрирующие
своеобразный взгляд на свободный двумерный
полёт тела под углом к горизонту.
Начальная скорость равноускоренно
движущейся точки равна 8 м/c. Через 0,5 с скорость
стала равной 5 м/c, а ещё через 0,5 с – 6 м/c.
Определите ускорение точки. (Заочная олимпиада
МФТИ, 1997.)
К решению. Конечно, здесь подвох,
характерный для старинного стиля задач типа «Что
тяжелее: килограмм пуха или килограмм железа?».
Некоторые учителя усматривают в этом
педагогический приём, развивающий
внимательность. Может быть, в физике есть
проблемы поинтереснее, чем поиск смысла,
скрытого в ребусе. И всё-таки. Здесь нужно
догадаться, что описанная ситуация невозможна
для одномерного движения, – это двумерное
криволинейное движение, подобное свободному
падению тела, брошенного под углом к горизонту, –
ускорение есть только по одному из направлений, а
по другому движение равномерно. Скорость можно
разложить на две составляющие: вдоль ускорения  y и поперёк
него y и поперёк
него  x.
Тогда условие задачи представится системой
кинематических соотношений: x.
Тогда условие задачи представится системой
кинематических соотношений:
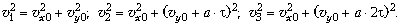 
Решая систему, находим  y0 = –6,4 м/с, y0 = –6,4 м/с,  x0 = 4,8 м/с, a = 10
м/с2. Действительно, это свободное падение с
начальной скоростью, направленной под углом
около 55° вверх к горизонту (при этом ускорение
направлено вниз). x0 = 4,8 м/с, a = 10
м/с2. Действительно, это свободное падение с
начальной скоростью, направленной под углом
около 55° вверх к горизонту (при этом ускорение
направлено вниз).
В семейном альбоме Кирилл нашел
фотографию, сделанную в юности отцом. На ней из
окна комнаты при открытом затворе запечатлён
фрагмент траектории летящей ракеты Октябрьского
салюта. После того как Кирилл узнал из
справочника, что начальная скорость ракеты равна
150 м/с, он взял линейку и сумел по фотографии
определить время горения этой ракеты. А вы
сумеете?
На примере одной этой задачи ученик
может понять суть движения под углом к горизонту
– класс задач, которые в некоторых школах вообще
не решают. Главная мысль состоит в том, что не
изменяется горизонтальная составляющая
скорости. Значит, по известному значению вектора
начальной скорости 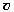 , изображённого в каком-либо масштабе и
направленного по касательной в начальной точке,
можно однозначно изобразить вектор конечной
скорости. Далее можно измерить длину
вертикальных составляющих2 скорости в
первом и втором положениях в тех единицах,
которые использовались при изображении вектора , изображённого в каком-либо масштабе и
направленного по касательной в начальной точке,
можно однозначно изобразить вектор конечной
скорости. Далее можно измерить длину
вертикальных составляющих2 скорости в
первом и втором положениях в тех единицах,
которые использовались при изображении вектора 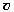 (например, в
миллиметрах). Теперь запишем известное
кинематическое соотношение (например, в
миллиметрах). Теперь запишем известное
кинематическое соотношение  y2 = y2 =  y1 – gt, откуда
получим t = ( y1 – gt, откуда
получим t = ( y1
– y1
–  y2)/g. y2)/g.
В приведённых задачах могут
использоваться тригонометрические
представления. Примеров таких задач много,
особенно для двумерного движения тел, брошенных
под углом к горизонту. И здесь возникает новая
проблема: зачастую темы тригонометрии изучаются
в математике чуть позже, чем они становятся
нужными в физике. Впрочем, не только
тригонометрия начинает тормозить программу.
Тригонометрия, черчение и прочее
Каждый преподаватель физики знает, что
поначалу нет потребности в полном объёме
тригонометрических знаний. Например, вполне
достаточно знания единиц углов и понятия синуса
как характеристики прямоугольного треугольника
(II в. н.э., Птолемей). Распространение функции на
углы больше 90° оставим математикам3. Для
освоения первичных знаний нужно не очень много
времени. 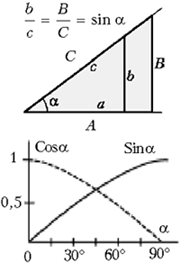
Рассказывая о синусе, нужно, конечно,
нарисовать основной график – по таблицам или с
помощью калькуляторов (конечно, инженерных). Не
забудем и об этимологии термина (sinus, лат., – выпуклость,
вздутие) – образность, как и мнемонические
правила (если этим не увлекаться, вымучивая
стишки по каждому поводу), снимают проблемы
усвоения даже сложных тем. О других функциях –
косинусе и тангенсе – можно упомянуть лишь
вскользь, подчеркнув необязательность
запоминания. Если к тому же вы не станете
торопиться с сиюминутным использованием этих
знаний, выдержав паузу, то через неделю весь
класс будет щеголять знанием вообще всех
тригонометрических функций. После этого вы
начинаете решать задачи с применением
тригонометрии, не останавливаясь, будто речь
идёт об очевидных и хорошо известных знаниях.
Например, можно смело вводить понятие
составляющих скорости движения (векторы будут
позже!) или определять длину горки по её высоте и
значению угла наклона. Попутно (например, на
очередном Дне здоровья) можно научиться измерять
высоту здания, или ширину реки, или даже скорость
течения реки, скорость волн и т.п., если этого не
делалось и не предполагается делать на уроках
географии. Конечно, любая нарочитость
предполагает внимательное отслеживание
ситуации, и если в классе возникло напряжение,
необходимо напомнить или коротко, без деталей,
пересказать материал заново – такова жизнь.
Ответ. 17,3 м/c.
Заодно поднимается важный вопрос о
том, как определить скорость падения капли по её
следу на стекле движущегося автомобиля, а также,
почему камень с крыши падает ускоренно, а капля,
пролетев почти километр высоты, имеет такую
маленькую скорость, сильно отличающуюся от 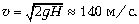 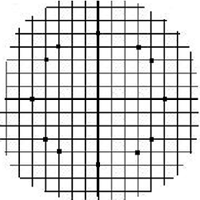
Можно обратить внимание на излишество
при использовании учениками чертёжных
принадлежностей на уроках физики, да и
математики, когда речь не идёт о специфических
задачах на построение с циркулем и линейкой.
Покажите, что, например, прекрасную окружность
радиусом 5 клеток можно нарисовать с
использованием знания египетского треугольника
со сторонами 3, 4, 5. Далее нарисуйте и окружность
радиусом 10 клеточек, важную дальше для
оперативного определения приближённых значений
синусов углов. Да и другие вспомогательные
рисунки вполне можно делать быстро, уверенными
линиями (а не «волосатыми» штрихами), развивая
твёрдость руки. Короче говоря, на своих уроках
необходимо полагаться прежде всего на тот
материал и те навыки, которые именно вы
развиваете у своих детей, не надеясь полностью на
математику, черчение, рисование, – там свои цели
и программы.
Препятствием на пути освоения
графического анализа задачи может явиться
неразвитое пространственное воображение и
неумение осмысленно рисовать – недоработка
начальной школы. Даже в старших классах
проявляется неумение определить масштаб
координатных осей при изображении конкретного
графика функции, определить шаг изменений
аргумента при расчёте значений функции. Ученики
часто не понимают закономерностей трансформации
графиков при изменении значений параметров
функций – смещение по оси X и Y,
растяжение, сжатие, поворот. Безусловно,
некоторые закономерности трансформации ещё не
изучались учениками в курсе математики, однако
опережающее развитие тоже важно: совсем неплохо,
когда знакомство с некоторыми прогрессивными
понятиями и идеями, до систематического изучения
которых ещё далеко, происходит чередой
нескольких поверхностных касаний – раньше, чем
ученик вступит в соответствующий сензитивный
период. Такие занятия производят необходимый
эффект по созданию в классе творческой атмосферы
и зарождению интереса или по крайней мере
любопытства. 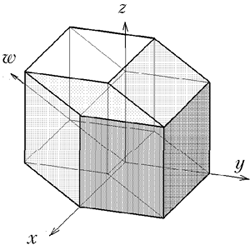
Например, успех имеет первоначально,
казалось бы, далёкий от физики опыт рисования
четырёхмерного куба на двумерной доске. Таким
образом, становится более понятным известный из
уроков черчения принцип объёмного изображения
предметов на плоскости. Действительно, мы просто
договариваемся, что изображённые оси X, Y,
Z являются взаимно перпендикулярными, хотя
рисуем их под определёнными углами друг к другу
(изометрия, диметрия, аксонометрия). Но так можно
договориться и о перпендикулярности не трёх, а
четырёх осей. Можно посчитать число вершин,
рёбер, сторон. Реальное знакомство с
таинственным термином «многомерность»
приобретает конкретность и становится занятием,
которому можно научиться4.
Далее ученикам можно предложить
индивидуальные задания по изображению самых
различных графиков функций различной сложности,
включая комбинации степенных и
тригонометрических функций. После выполнения
задания результаты и характерные ошибки
тщательно разбираются и, самое важное, делаются
попытки подбора физических ситуаций,
реализующих эти типы движений. В результате
таких отвлечений удаётся разрушить барьер между
понятиями математики и физики и овладеть
графическими методами решения задач.
Графики в решении задач
Конечно, совершенно необходимо
развить умение определять знак и относительные
значения скорости по наклону касательной на
пространственно-временном графике (позже, к 11-му
классу, мы назовём его мировой линией).
Впрочем, можно научиться определять и абсолютные
значения скорости на оцифрованном графике
(техника графического дифференцирования). Такие
упражнения очень важны – учащиеся будут уметь
анализировать движение уже по виду кривой. Не
буду останавливаться на этом вопросе (например,
для равнопеременного движения он хорошо изложен
у Ю.А.Селезнёва [2]). 
Из пушки делают две серии выстрелов,
наклонив ствол под углами 30° и 40° к горизонту. В
каком случае попадания снарядов будут более
кучными, если разброс вызван в основном не
различием начальных скоростей снарядов, а
неточностью прицеливания? Сопротивлением
воздуха можно пренебречь. (Квант, 1972, № 3.)
К решению. Запишем формулу для
дальности полёта s и изобразим её как
функцию угла наклона. Из рисунка ясно видно, что
при углах, близких к 45°, разброс значений
дальности 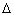 s
при изменении угла наименьший. Значит, разброс
при 40° будет меньше, чем при 30°. s
при изменении угла наименьший. Значит, разброс
при 40° будет меньше, чем при 30°.
На графике представлена зависимость
от времени силы F, действующей вдоль прямой,
на тело массой m = 2 кг, движущееся по этой
прямой с начальной скоростью  0. В какой момент времени
скорость тела была наибольшей по абсолютной
величине? Рассмотрите возможные варианты
ответов для случаев, когда модуль | 0. В какой момент времени
скорость тела была наибольшей по абсолютной
величине? Рассмотрите возможные варианты
ответов для случаев, когда модуль | 0| равен 11 м/с, 10 м/с и
12 м/с. 0| равен 11 м/с, 10 м/с и
12 м/с.
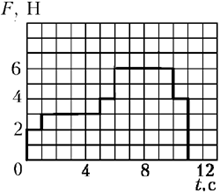
К решению
1. Начальная скорость и ускорение
направлены одинаково. Скорость нарастает, и
максимальное значение всегда достигается в
конце промежутка времени:
| m1|
= m1|
=  m1 = 11 + 23
= 34 (м/с); | m1 = 11 + 23
= 34 (м/с); | m2|
= m2|
=  m2 = 10 + 23
= 33 (м/с); | m2 = 10 + 23
= 33 (м/с); |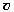 m3|
= m3|
=  m3 = 12 + 23
= 35 (м/с). m3 = 12 + 23
= 35 (м/с).
2. Начальная скорость и ускорение
направлены противоположно друг другу. В
зависимости от начальной скорости максимальное
значение модуля скорости достигается не
обязательно в конце рассматриваемого промежутка
времени:
|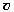 m1|
= 12 м/с – в конце промежутка времени; m1|
= 12 м/с – в конце промежутка времени;
|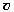 m1|
= 13 м/с – в конце промежутка времени; m1|
= 13 м/с – в конце промежутка времени;
|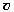 m1|
= 12 м/с – в начале промежутка времени. m1|
= 12 м/с – в начале промежутка времени.
А вот ещё важный для будущего и
увлекательный тип задач с графическим поиском
сложного решения. 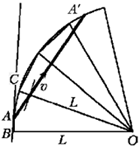
На гладкой горизонтальной
поверхности бильярда установлены три гладкие
вертикальные стенки, образующие равнобедренный
треугольник. Шару А сообщают скорость  под углом под углом 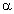 к короткой стороне. Оцените
время между двумя последовательными ударами
шайбы о короткую стенку, если все удары со
стенками абсолютно упругие. (Зональная
олимпиада, 1997 г., Ростов-на-Дону.) к короткой стороне. Оцените
время между двумя последовательными ударами
шайбы о короткую стенку, если все удары со
стенками абсолютно упругие. (Зональная
олимпиада, 1997 г., Ростов-на-Дону.)
К решению. Стандартный приём
решения задач – построение зеркального
изображения (см., например, [3]). Достроим ещё
несколько треугольников, как показано на
рисунке. В этом случае переход траектории шара из
одного треугольника в другой описывает движение
по закону зеркального отражения. Видно, что при
данном построении шар возвращается на короткую
стенку после трёх соударений.
Добавлю, что желательно на чуть более
позднем этапе освоения графиков функций
познакомить учащихся с таким важным сегодня
инструментом, как интегрированные
математические пакеты. Не стоит, наверное,
перегружать младших школьников освоением таких
сложных пакетов, как MathCad, MatLab, Maple.
Вполне можно обойтись простой и компактной
программой типа Derive for Windows (около 800 кбит в
архивированном виде, DOS-версия ещё короче, но
сейчас уже не актуальна). Прежде всего эта
программа позволяет быстро, без использования
специального синтаксиса, получить на экране
двух- и трёхмерные графики функций, задаваемых
как в прямоугольных, так и в полярных
координатах. Можно наложить графики друг на
друга и пр. Иногда школьники используют Advanced
Grapher и другие подобные программы. Для изучения
физики и подготовки рефератов, докладов и
презентаций использование таких математических
пакетов очень удобно и полезно, наряду с хорошими
(научными) калькуляторами. А на уроках математики
и информатики вполне могут быть свои правила.
Сложные типы движения
Энергичное знакомство с
существованием более сложных законов изменения
скорректирует и закрепит процесс формирования
понятия скорости, ускорения и даже более высоких
характеристик движения физических величин в
терминах малых приращений.
Точка движется по прямой, согласно
уравнению x = 6 + 0,125t3. Определите
скорость к моменту времени 6 с от начала движения.
(Турчина Н.В. и др. 3800 задач по физике. – М.:
Дрофа, 2000. Задача упрощена для демонстрации.)
К решению. Определим скорость как
отношение интервалов изменения координаты и
времени. Учтём и то, что скорость в данный момент
будет определена тем точнее, чем меньший
интервал времени мы возьмём в окрестности
данного момента времени. Мы записывали такое
отношение и ранее, но отвлечённо, а теперь нужно
проделать это практически.
Запишем:
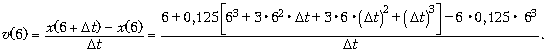
Устремляя 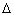 t к нулю, получим результат: t к нулю, получим результат:
 (6) = 0,125 • 3
• 62 = 13,5 (м/c). (6) = 0,125 • 3
• 62 = 13,5 (м/c).
Важно, что идеи дифференциального и
интегрального исчислений вполне могут быть
восприняты учениками на самых начальных этапах
изучения физики. Совсем необязательно при этом
называть процесс определения приращения
значения физической величины в аналитическом
виде или с использованием графика 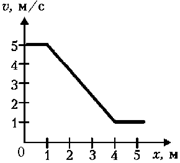 вычислением
дифференциала, а суммирование бесконечно
малых – интегрированием. вычислением
дифференциала, а суммирование бесконечно
малых – интегрированием.
К решению. Учтём, что ускорение, по
определению, есть отношение 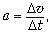 которое необходимо выразить
через координаты точки (впоследствии такой приём
станет стандартным): которое необходимо выразить
через координаты точки (впоследствии такой приём
станет стандартным):
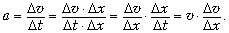
Последнее соотношение уже можно
использовать для вычисления, выделив на графике
окрестность точки с координатой x = 3 м.
Получим:
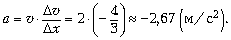
Кинематика вращательного
движения
Для первоначального знакомства с
характеристиками вращения, пожалуй, вполне
достаточно понятий периода вращения, частоты,
угловой скорости, углового ускорения и связи
этих величин с радиусом вращения. Здесь важно
решить стандартные примеры расчёта угловых
скоростей вращения Земли, стрелок часов,
вычислить линейные скорости точек экватора и
точек Земли на вашей широте. Например, на широте
Саратова находятся ещё и такие города, как
Берлин, Лондон, Калгари, Чита, Иркутск (сos52° = 0,61).
Непременно нужно сравнить формулы равномерного
и равнопеременного движений по прямой и по
окружности и обратить внимание на их аналогию
при замене линейных характеристик на угловые.
Последнее экономит память учащихся, а для
некоторых учеников способствует прочному
запоминанию всего блока формул. Вот типовые
упражнения на эту тему.
Ответ. Через 10 с.
Полезно переформулировать задачу в
терминах, например, затормозившего автомобиля, с
известными начальной скоростью и длиной пути
торможения.
Пуля современного пистолета ПМ
вращается в полёте с частотой 3000 об/с. Оцените,
сколько оборотов имеет нарезка внутри ствола,
если скорость вылета пули близка к 600 м/c, а длина
пути в стволе около 12 см.
К решению. Надо использовать
среднее значение скорости пули в стволе, приняв
движение равнопеременным – для оценки.
Получается примерно
0,6 оборота.
Совершенно необходимо обратить
внимание на зависимость величины линейной
скорости точки от расстояния до мгновенной оси
вращения на примере железнодорожного колеса,
фрикционной или зубчатой передачи, а также на
процедуру определения полной скорости любой
точки катящегося колеса. Всегда полезны и задачи,
вызывающие дискуссию. 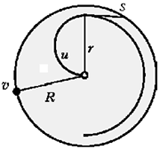
Одновременно два точечных тела
начинают двигаться: первое по окружности
радиусом R с постоянной по модулю скоростью  ; второе – из центра
той же окружности со скоростью u = 0,8 ; второе – из центра
той же окружности со скоростью u = 0,8 . Скорость второго тела
постоянно направлена на первое тело. На каком
минимальном расстоянии окажутся тела через
достаточно большое время? (Зональная олимпиада
1999 г., Ростов-на-Дону.) . Скорость второго тела
постоянно направлена на первое тело. На каком
минимальном расстоянии окажутся тела через
достаточно большое время? (Зональная олимпиада
1999 г., Ростов-на-Дону.)
К решению. После обсуждения
приходим к выводу, что установившимся движением
будет движение обоих тел по двум концентрическим
окружностям с одинаковыми угловыми скоростями:
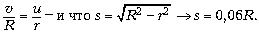
Вызывает сомнение целесообразность
рассмотрения в разделе «Кинематика» такого
сложного понятия, как нормальное
(центростремительное) ускорение. Больший эффект
достигается при введении этой величины в
динамике, после знакомства с причинами,
вызывающими движение тела. Во-первых, к этому
времени школьники набирают достаточный запас
математической подготовки и готовы к полному
восприятию векторных величин. Во-вторых, после
знакомства с описанием силовых характеристик и
уравнением движения, процедура разложения
вектора ускорения при плоском криволинейном
движении на две составляющие – нормальную и
тангенциальную – представляется совершенно
естественной. Именно к этому времени становится
актуальным рассмотрение ситуаций, в которых
возникает задача вычисления значений этих
составляющих ускорения.


Н.Кращин. Скорость cвета. http://elementy.ru/lib/exhibition
Заключение: не увлекаться
кинематикой – динамика интереснее!
Есть и ещё один довод в пользу
ограниченного первоначального знакомства с
кинематикой. Введение основных кинематических
понятий осуществляется на начальном этапе
изучения физики. В связи с этим нет
необходимости, а порой даже опасно, отводить на
эти занятия значительный отрезок времени и
добиваться от учеников законченности понимания
темы. Следует признать мнение школьников (и
студентов!) о кинематике как об одном из самых
скучных разделов физики. Это мнение существует и
возникает в каждом поколении, даже если оно не
соответствует действительности. В самом деле,
казалось бы, нет особенной сложности в первичном
усвоении понятий скорости, ускорения,
координаты, траектории. Практически всеми этими
понятиями люди пользуются в обиходе, поэтому
даже при интересной организации семинара
гораздо большее любопытство учеников вызывает
не математически насыщенный расчёт параметров
уже заданных движений, а причины осуществления
этих движений и вопросы их реализации в природе.
Учитывая этот психологический настрой, полезнее
осуществить как можно более стремительный
прорыв в динамику, упредив момент спада интереса
к предмету. Дальнейшее изучение механики и
других разделов физики, постоянное обращение к
кинематическим закономерностям поможет
ученикам (и учителю) скорректировать недостатки
понимания и пробелы в технике. Пусть осталась
непроработанной тема относительности (см.
«Квант» № 9/1989, 2/1990,1/2005), мало уделено внимания
векторному характеру кинематических законов с
интереснейшими задачами на эту тему (одна из
чудесных задач, правда, для старших классов,
разобрана Л.И.Ефимовой в «Физике» № 4/05, с. 27–28, см.
также задачу Всероссийской олимпиады 2002 г.).
Можно вновь обратиться к упущенным подробностям,
но уже при наличии мотивации.
Последнее замечание позволяет
сформулировать важное правило ведения урока или
семинара: чем скучнее представляется ученикам
тема занятия, тем интереснее и эффективнее в
данной аудитории должны быть предлагаемые
примеры и задачи. Готовясь к семинару в четырёх
группах, когда в каждой будет разобрано максимум
5–6 задач, автор отбирает до двадцати задач на
карточках, где иногда кроме решения указаны и
варианты, и сценарий представления данной
задачи, а также выход на другие темы. Такой способ
мобильнее, чем запись примеров в схему урочного
плана, имеется возможность мгновенно отследить
ситуацию заинтересованности и возможностей
класса и заменить один плановый пример другим,
тоже запланированным. Задачи домашних заданий и
самостоятельных работ предлагаются из одного
или нескольких заранее оговорённых сборников,
имеющихся в классе в бумажном или электронном
варианте. Ну а самостоятельная работа
продвинутых учащихся не регламентируется, а
только поощряется и стимулируется
факультативными занятиями и личными беседами.
Вопросы для самоконтроля
1. Художник рисует на холсте простой
цветок клевера, расположившись лицом к берегу на
плывущем судне. Изобразите примерную траекторию
кончика карандаша в системе координат, связанной
с берегом.
2. Известно, что тела, брошенные под
углом к горизонту со скоростью меньше второй
космической, летят по эллипсу. Покажите, что для
малых скоростей этот эллипс действительно может
быть заменён параболой.
3. Опишите устройство спидометра в
автомобиле. Каким образом он, не имея внутри
процессора, фиксирует именно мгновенную, а не
среднюю скорость?
4. Означает ли линейная связь величин
их пропорциональность друг другу?
Литература
1. Кирпичёв В.Л. Беседы о механике.
– М.– Л.: ГИТТЛ, 1951 (и др. издания).
2. Селезнёв Ю.А. Основы
элементарной физики. Гл. I, § 1. – М.: Наука, 1974 (и др.
издания).
3. Штейнгауз Г. Математический
калейдоскоп. – М.: Наука, 1981.
____________________
1 Может быть, в этом «пунктик» автора.
Однако в последнее время слишком часты вздохи о
книгах без формул, но якобы изобилующих
наглядностью. Уж и впечатление-то они произвели
неизгладимое, и природа заиграла всеми красками.
И теперь, дескать, так только и нужно, а некоторые
так и делают. Для чиновника эти «факты» очень
удобны, поскольку укрепляют в верности курса
реформ на упрощение и сокращение. Трудно, однако,
не признать пользы и популярности книг
Я.И.Перельмана, где каждая история подкреплена
практической оценкой. И если удаётся поговорить
с автором очередного подобного высказывания, то
оказывается, что от такой книги осталась-то лишь
иллюзия понимания, как от публичной лекции
академика. Ценю рассуждения о красоте природы и
об истории открытий, но стараюсь, чтобы мои
ученики «ведали начала».
2 В последние годы используют термин
«компонент» и в женском роде, так что
«компонента» и «составляющая» оказались
взаимозаменяемыми.
3 Конечно, знание теоремы
косинусов не помешает для решения некоторых
задач. И всё же можно подождать довольно долго. А
затем подавайте теорему косинусов как обобщение
теоремы Пифагора на произвольные (а не только на
прямоугольные) треугольники. Математики так
обычно не делают.
4 Одновременно не мешает
упомянуть о различии между условностями
инженерной графики и субъективного рисунка в
искусстве. В любом учебнике по живописи можно
получить сведения о художественных приёмах
изображения объёмных предметов или их
расположения в пространстве посредством
перспективы – от Дюрера до Раушенбаха. Здесь всё
зависит от вашего личного кругозора, но всё это
почти всегда за пределами урока.
Продолжение в № 19 |