Продолжение. См. № 2, 4, 6,
8, 10, 12, 16,
18/06
Проф. М.Б.МЕНСКИЙ,
ФИАН им. П.Н.Лебедева, г. Москва
mensky@lebedev.ru
Странности квантового мира и
тайна сознания
(Печатается выборочно и в сокращении по книге
М.Б.Менского «Человек и квантовый мир (странности
квантового мира и тайна сознания)» (Фрязино: Век2,
2005; vek-2@mail.ru).)
Часть II. КВАНТОВЫЙ МИР И СОЗНАНИЕ
В этой части книги мы попытаемся
проложить путь от квантовой механики к теории
сознания. Теперь мы остановимся на
концептуальных проблемах (парадоксах) квантовой
механики, связанных с особенностями квантовых
измерений. Для решения этих проблем оказывается
необходимым включить в рассмотрение не только
измерительный прибор, но и наблюдателя
(экспериментатора), и его сознание. Отсюда
вырастает целый комплекс новых идей, которые
могут служить базой для новой теории сознания.
Эта теория бросает свет на феномен жизни и
позволяет понять необычные свойства сознания,
которыми оно обладает в особых состояниях,
похожих на транс. Тем самым квантовая механика
перекидывает мост между естественными науками, с
одной стороны, и гуманитарными науками, а также
ненаучными методами познания духовной жизни
человека – с другой. Сознание (точнее, самый
глубокий, или примитивный, пласт сознания)
оказывается общим элементом этих двух сфер
познания.
Математические формулы, встречающиеся
в этой части, очень просты, причём одна и та же
формула встречается несколько раз в разных
контекстах, что облегчает понимание её смысла.
Читатели-гуманитарии, которые не хотят иметь
дело даже с простыми формулами, могут пропускать
как отдельные формулы, так и целые разделы. Эта
часть написана так, чтобы такие пропуски не
слишком затрудняли понимание. Ближе к концу
книги математические формулы вообще перестанут
встречаться. Для тех же, кто, наоборот,
интересуется математическим содержанием
затронутых вопросов, даются ссылки на разделы
первой части книги и на приложения, в которых
применяется более сложный математический
аппарат.
Гл. 3. ПАРАДОКСЫ КВАНТОВЫХ
ИЗМЕРЕНИЙ
Одна из особенностей квантового
измерения состоит в том, что квантовую систему
невозможно измерить (т.е. получить какую бы то ни
было информацию о ней), не возмутив при этом её
состояние, причём тем сильнее, чем больше
информации извлекается при измерении. Это,
конечно, хорошо известно и количественно
трактуется обычно при помощи соотношения
неопределённостей.
Известно также, что, даже зная
состояние системы совершенно точно, результат
измерения в ней лишь в исключительных случаях
можно предсказать достоверно. В общем случае
можно лишь рассчитать вероятность того или иного
результата измерения, т.е. знать, как часто при
измерении будет получаться данный результат,
если много раз проводить одно и то же измерение,
каждый раз приготовляя одно и то же начальное
состояние измеряемой системы. А большего нам
знать в общем случае не дано. Для практических
целей этого вполне достаточно. Все
(вероятностные) предсказания, основанные на
таких расчётах, хорошо подтверждаются, и в этом
смысле измерения квантовых систем не
представляют никакой проблемы.
На языке формул простейшее измерение,
различающее две альтернативы, представляется
так (детали можно найти в приложении А). Пусть  1 –
состояние, соответствующее первой альтернативе,
а
1 –
состояние, соответствующее первой альтернативе,
а  2 –
состояние, соответствующее второй альтернативе.
Пусть перед измерением система находилась в
состоянии1 c1
2 –
состояние, соответствующее второй альтернативе.
Пусть перед измерением система находилась в
состоянии1 c1 1 + c2
1 + c2 2. Тогда с вероятностью
|c1|2 измерение даст первый
результат, и система окажется после измерения в
состоянии
2. Тогда с вероятностью
|c1|2 измерение даст первый
результат, и система окажется после измерения в
состоянии  1,
а с вероятностью |c2|2 измерение
даст второй результат, и система окажется после
измерения в состоянии
1,
а с вероятностью |c2|2 измерение
даст второй результат, и система окажется после
измерения в состоянии  2.
2.
Используя такую картину квантового
измерения, можно вполне успешно работать в
квантовой механике и никогда не столкнуться с
концептуальными проблемами. Многие физики не
знают, да и знать не хотят, что это за проблемы. А
они действительно необычны, хотя бы потому, что
наиболее ясные их формулировки имеют форму
парадоксов, знаменитых квантово-механических
парадоксов, например, «Парадокс кота Шрёдингера»
и «Парадокс друга Вигнера». Физики же
практического склада не интересуются
парадоксами, коль скоро задачи, которые им нужно
решить, можно сформулировать корректно.
Давайте, однако, вспомним, что это за
парадоксы, на которые считали необходимым
тратить время и силы такие выдающиеся физики, как
авторы упомянутых парадоксов Шрёдингер и Вигнер,
а также Эйнштейн, Бор, Гейзенберг, Паули, Уилер,
ДеВитт и многие другие.
3.1. Парадокс кота Шрёдингера
Парадокс шрёдингеровского кота
достаточно широко известен. В закрытом ящике
находится кот, а рядом с ним, в том же ящике, –
атом радиоактивного изотопа, счётчик продуктов
распада и устройство, которое при срабатывании
счётчика разбивает ампулу с ядом. Пока атом не
распался, с котом всё в порядке, но когда атом
распадается, под действием продуктов распада
срабатывает счётчик, по его сигналу специальное
устройство разбивает ампулу, и кот гибнет от яда.
Далее вступает в силу вероятностный
характер квантовой механики. Неизвестно, когда
атом распадётся, в каждый данный момент имеется
лишь определённая вероятность распада. А точнее,
в каждый данный момент атом находится в
суперпозиции двух состояний: состояния, когда он
ещё не распался, и состояния, когда он распался. И
в результате возникает парадокс. Подходя к
закрытому ящику, мы должны, согласно законам
квантовой механики, считать, что система (атом +
кот) находится в суперпозиции двух состояний:
нераспавшийся атом + живой кот и распавшийся атом
+ мёртвый кот.
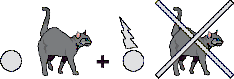
Парадокс кота Шрёдингера. Жизнь
кота зависит от того, распалось или ещё не
распалось ядро радиоактивного элемента.
Согласно квантовой механике, система ядро + кот
находится в суперпозиции двух состояний:
нераспавшееся ядро и живой кот + распавшееся ядро
и мёртвый кот. Но, посмотрев на эту систему, мы
увидим лишь одну компоненту этой суперпозиции
Открыв ящик, мы, разумеется, никогда
никакой суперпозиции не обнаружим, а увидим либо
живого кота (и ещё не распавшийся атом), либо
мёртвого кота (и уже распавшийся атом). Описание
системы зависит, следовательно, от того, открыли
мы ящик или ещё не открыли. В этом и состоит
парадокс.
В более общих терминах описание
системы после измерения зависит от того, осознал
наблюдатель результат измерения или нет. В
случае шрёдингеровского кота измерением можно
считать всю описанную процедуру, а результатом
измерения – то, что наблюдатель видит, открыв
ящик. При этом драматическая ситуация с гибелью
кота призвана лишь усилить психологическое
воздействие на того, кто рассматривает эту
ситуацию. На самом деле парадоксальность
возникает в любом квантовом измерении:
пока результат измерения не осознан
наблюдателем, этот наблюдатель описывает
состояние системы как сосуществование
(суперпозицию) двух или более альтернатив. Если
же результат измерения уже осознан, тот же
наблюдатель описывает состояние как одну из
альтернатив.
Заметим, что происходящее нельзя
объяснить лишь отсутствием у наблюдателя
информации о результате измерения. Такое
незнание результата измерения, которое
сменяется знанием, если этот результат осознан,
ничего удивительного собой не представляет и
сплошь и рядом встречается и в классической
физике, и в обыденной жизни. В квантовой механике
всё гораздо серьёзнее, т.к. можно строго доказать,
в том числе экспериментально, что перед
измерением на самом деле сосуществуют все
альтернативы (мы поговорим об этом подробнее в
разделе 4.1), и пока наблюдатель не осознал, какой
результат дало измерение, он обязан, следуя
законам квантовой механики, описывать состояние
системы как сосуществование (суперпозицию) всех
альтернатив. Мы ещё будем возвращаться к этому
трудному для понимания пункту, чтобы сделать его
максимально ясным.
3.2. Парадокс друга Вигнера
Парадоксальность происходящего при
квантовом измерении ещё более подчёркивается в
«Парадоксе друга Вигнера». Вигнер в своей работе
1961 г.2 рассмотрел ситуацию, в которой не он
сам, а его друг проводит измерение некоторой
квантовой системы, а потом сообщает ему
результат измерения. Результат в конечном счёте
сводится к тому, что система находится в одном из
двух состояний –  1 или
1 или  2. Экспериментатор узнаёт о
состоянии системы по тому, видит ли он вспышку
света в соответствующем измерительном
устройстве.
2. Экспериментатор узнаёт о
состоянии системы по тому, видит ли он вспышку
света в соответствующем измерительном
устройстве.
И в этом случае, как и в случае кота
Шрёдингера, перед измерением система находится в
состоянии, являющемся суперпозицией состояний  1 и
1 и  2. А как
описать состояние, в котором система находится
после измерения? Оказывается, это опять зависит
от сознания наблюдателя. Если экспериментатор
ещё не посмотрел на прибор, то он описывает
состояние как суперпозицию
2. А как
описать состояние, в котором система находится
после измерения? Оказывается, это опять зависит
от сознания наблюдателя. Если экспериментатор
ещё не посмотрел на прибор, то он описывает
состояние как суперпозицию  1 и
1 и  2. Если уже посмотрел, то либо как
2. Если уже посмотрел, то либо как  1, либо как
1, либо как  2 (в
зависимости от того, что именно он увидел).
Описание состояния системы зависит от того,
осознал ли экспериментатор состояние системы
или нет.
2 (в
зависимости от того, что именно он увидел).
Описание состояния системы зависит от того,
осознал ли экспериментатор состояние системы
или нет.
Это мы видели уже в парадоксе
шрёдингеровского кота. Однако Вигнер вносит
новый элемент за счёт того, что его
друг-экспериментатор передаёт информацию об
измерении ему, Вигнеру. Пока Вигнер не получил
этой информации, он описывает состояние системы
как суперпозицию  1 и
1 и  2. Получив информацию, описывает
уже по-другому: либо как
2. Получив информацию, описывает
уже по-другому: либо как  1, либо как
1, либо как  2 (в зависимости от того, каково
содержание переданной информации). Значит,
описание состояния системы Вигнером зависит от
того, вошла ли в его сознание информация о
результате измерения, переданная ему его
другом-экспериментатором.
2 (в зависимости от того, каково
содержание переданной информации). Значит,
описание состояния системы Вигнером зависит от
того, вошла ли в его сознание информация о
результате измерения, переданная ему его
другом-экспериментатором.
Парадоксальность ситуации
подчёркивается следующим рассуждением. Вигнер
говорит: «Если после окончания эксперимента я
спрошу моего друга: „Что ты чувствовал по поводу
вспышки света перед тем, как я тебя спросил?” –
он ответит: „Я уже сказал тебе, я видел (не видел)
вспышку”. Другими словами, вопрос о том, видел
или не видел он вспышку, был уже решён в его уме
прежде, чем я спросил его». Чтобы ясно увидеть,
что здесь странного (парадоксального), переведём
это на язык формул.
Пусть состояние измеряемой системы
перед измерением было c1 1 + c2
1 + c2 2, а
состояние прибора
2, а
состояние прибора  0.
Тогда состояние составной системы, состоящей из
измеряемой системы и прибора, перед измерением
представляется вектором состояния
0.
Тогда состояние составной системы, состоящей из
измеряемой системы и прибора, перед измерением
представляется вектором состояния
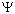 0
=
0
= 
 0 = (c1
0 = (c1 1 + c2
1 + c2 2)
2) 0 = c1
0 = c1 1
1 0 + c2
0 + c2 2
2 0.
0.
Обозначим через  1 то состояние измерительного
прибора, в котором происходит вспышка, и через
1 то состояние измерительного
прибора, в котором происходит вспышка, и через
 2 –
состояние, в котором вспышки не происходит. Тогда
результат измерения, воспринимаемый
наблюдателем, описывается либо вектором
2 –
состояние, в котором вспышки не происходит. Тогда
результат измерения, воспринимаемый
наблюдателем, описывается либо вектором  1
1 1 (если он видит
вспышку), либо
1 (если он видит
вспышку), либо  2
2 2 (если он её не
видит). Первое означает, что прибор из состояния
2 (если он её не
видит). Первое означает, что прибор из состояния  0 перешёл в
состояние
0 перешёл в
состояние  1, а
измеряемая система оказалась в состоянии
1, а
измеряемая система оказалась в состоянии  1. Второе
интерпретируется аналогично.
1. Второе
интерпретируется аналогично.
Такие состояния составной системы
(состоящей из двух подсистем), как  1 =
1 =  1
1 1 или
1 или  2 =
2 =  2
2 2, называются факторизованными.
В них каждая из подсистем находится в
определённом состоянии, т.е. характеризуется
вектором состояния3.
2, называются факторизованными.
В них каждая из подсистем находится в
определённом состоянии, т.е. характеризуется
вектором состояния3.
Предположим, однако, что измерительный
прибор уже сработал, но наблюдатель ещё не
посмотрел на прибор. Тогда состояние полной
системы (включающей измеряемую систему и прибор)
получается из начального состояния действием
линейного оператора эволюции или решением
линейного уравнения Шрёдингера. Это обязательно,
просто в силу линейности этой операции, даёт
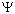 = с1
= с1 1
1 1 + с2
1 + с2 2
2 2 = с1
2 = с1 1 + с2
1 + с2 2.
2.
Такое состояние в отличие от
факторизованного называется запутанным,
или квантово-коррелированным. В запутанном
состоянии каждая из подсистем не находится ни в
каком определённом состоянии. В данном случае ни
измеряемая система, ни прибор ни в каком
определённом состоянии не находятся. Имеется
лишь квантовая корреляция, которую можно
сформулировать так: если прибор находится в
состоянии  1,
то измеряемая система – в состоянии
1,
то измеряемая система – в состоянии  1, а если прибор
находится в состоянии
1, а если прибор
находится в состоянии  2, то измеряемая система – в
состоянии
2, то измеряемая система – в
состоянии  2
(подробнее о квантовой корреляции см. Приложение
А.5).
2
(подробнее о квантовой корреляции см. Приложение
А.5).
Пока наблюдатель не осознал результат
наблюдения, он руководствуется лишь тем, что
диктуется законами квантовой механики, и поэтому
должен описывать состояние полной системы
вектором y. Если же он осознал результат
измерения, то будет описывать состояние либо
вектором 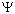 1=
1=
 1
1 1, либо вектором
1, либо вектором 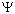 2 =
2 =  2
2 2, в зависимости от
того, какой именно результат он наблюдает.
2, в зависимости от
того, какой именно результат он наблюдает.
Вигнер описывает состояние вектором 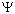 , пока его друг не
сообщил ему результат измерения, но после
сообщения – одним из векторов
, пока его друг не
сообщил ему результат измерения, но после
сообщения – одним из векторов 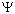 1,
1, 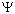 2. После того, как друг Вигнера
(экспериментатор) ответил ему на вопрос: «Что ты
чувствовал по поводу вспышки света перед тем, как
я тебя спросил?» Вигнер должен сделать вывод, что,
даже не получив сообщения о результате
измерения, но зная, что измерение произошло и его
друг знает результат измерения, он должен
описывать состояние одним из векторов
2. После того, как друг Вигнера
(экспериментатор) ответил ему на вопрос: «Что ты
чувствовал по поводу вспышки света перед тем, как
я тебя спросил?» Вигнер должен сделать вывод, что,
даже не получив сообщения о результате
измерения, но зная, что измерение произошло и его
друг знает результат измерения, он должен
описывать состояние одним из векторов 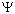 1,
1, 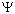 2 (не зная,
правда, каким именно из этих двух). В этом случае
описание состояния Вигнером определяется его
знанием того, что его друг-экспериментатор
посмотрел на прибор, т.е., что в сознание его друга
вошла информация о результате измерения.
2 (не зная,
правда, каким именно из этих двух). В этом случае
описание состояния Вигнером определяется его
знанием того, что его друг-экспериментатор
посмотрел на прибор, т.е., что в сознание его друга
вошла информация о результате измерения.
Ещё один нюанс появляется, если
рассмотреть ситуацию, когда никакого живого
наблюдателя (друга Вигнера) около прибора нет. В
этом случае просто в силу линейности уравнений
квантовой механики Вигнер (как и любой другой
физик на его месте) должен описывать состояние
после измерения вектором 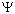 = с1
= с1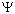 1 + с2
1 + с2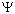 2. Если «измерительный
прибор» является микроскопическим, например,
атомом, то с помощью дополнительных опытов можно
убедиться (по наличию интерференционных
эффектов), что правильное описание состояния
действительно даётся вектором
2. Если «измерительный
прибор» является микроскопическим, например,
атомом, то с помощью дополнительных опытов можно
убедиться (по наличию интерференционных
эффектов), что правильное описание состояния
действительно даётся вектором 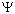 , а не
, а не 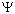 1 или
1 или 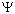 2. В случае макроскопического
прибора такую проверку произвести нельзя, однако
вектор
2. В случае макроскопического
прибора такую проверку произвести нельзя, однако
вектор 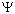 = с1
= с1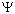 1 + с2
1 + с2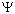 2 можно
вывести теоретически, опираясь только на
линейность уравнений квантовой механики
(например, уравнения Шрёдингера).
2 можно
вывести теоретически, опираясь только на
линейность уравнений квантовой механики
(например, уравнения Шрёдингера).
Из всего этого в статье Вигнера
делался вывод, что живой наблюдатель играет
особую роль в квантовой механике, нарушая
каким-то образом линейный характер эволюции.
Если в сознание наблюдателя входит информация о
результате измерения, то описание состояния
становится таким, которое не может получиться
при эволюции, описываемой линейным оператором.
Статья Вигнера была написана давно, и
её аргументы кажутся, на первый взгляд, наивными.
На самом деле, однако, они вскрывают глубокие и
действительно весьма своеобразные черты
квантовых измерений, которые хорошо понятны с
чисто формальной, математической, стороны, но
плохо уживаются с нашей интуицией.
Для дальнейшего изложения наиболее
важным выводом из сказанного является то, что
только осознание альтернативного результата
измерения приводит к тому, что из двух (или более)
членов суперпозиции остаётся лишь один. Это, в
свою очередь, означает, что сознание наблюдателя
следует явным образом учитывать при анализе
квантового измерения, без такого учёта описание
квантового измерения является неполным.
Роль сознания в квантовом измерении
можно аргументировать и другими способами.
Упомянем некоторые из них.
3.3. Роль сознания наблюдателя
Итак, основой описания измерения в
квантовой механике является, во-первых,
вероятностное распределение по альтернативным
результатам измерения и, во-вторых, постулат
редукции, т.е. переход от суперпозиции
альтернатив к одной из этих альтернатив. Такое
описание позволяет дать ответы на все вопросы,
обычно задаваемые в физике, и предсказать
(вероятностным образом) поведение любых реальных
физических систем. Никакие парадоксы или
концептуальные проблемы не мешают этим
предсказаниям. Квантовая теория измерений
хорошо работает.
Почему же возникают парадоксы, и с чем
связано их возникновение? Нетрудно заметить, что
парадоксы возникают каждый раз, когда
упоминаются не только объективные аспекты
измерения (состояние системы, состояние прибора),
но и субъективный его аспект (что видит или
сознаёт наблюдатель). Это чрезвычайно важно.
Хорошо работающая часть квантовой теории
измерений – та, которая остаётся после
устранения субъективного элемента, сознания
наблюдателя. Заметим, что после устранения
наблюдателя нет никакой причины выделять один
результат измерения (один член суперпозиции), а
следует работать со всем множеством
альтернативных результатов измерения,
сопоставляя каждому из них его вероятность.
Но что же представляет собой этот
субъективный элемент, как он соотносится с
объективными элементами квантовой теории
измерений? При наивном подходе можно было бы
думать, что сознание – это состояние некоторой
материальной системы, скажем, мозга или
некоторой структуры в мозге. Однако это не так,
или не совсем так. Дело в том, что любую
материальную систему, которая так или иначе
отражает в своём состоянии результат измерения,
можно включить в понятие прибора как его часть. А
сознание наблюдателя в контексте квантовой
теории измерений – это то, что остаётся за
пределами прибора. Более того, описание
измерения существенно не изменится, если
какие-то части прибора, отражающие результат
измерения, описывать как части измеряемой
системы. Это относится и к тем структурам в мозге,
которые отражают результат измерения.
Ещё Гейзенберг заметил, что нельзя
однозначно определить границу между измеряемой
системой и прибором (точнее, между измеряемой
системой и измеряющей средой, в которую следует
включить и наблюдателя как материальную
систему). Действительно, описание измерения
принципиально не изменится, если включить в
измеряемую систему и некоторые части прибора,
состояние которых зависит от результата
измерения.
Можно, например, отнести к измеряемой
системе чувствительный элемент прибора,
непосредственно взаимодействующий с измеряемой
системой, а роль прибора отвести лишь к остальным
его частям. Но можно отнести к измеряемой системе
также и регистрирующую часть прибора, его
стрелку. Можно пойти ещё дальше и отнести к
измеряемой системе фотоны, летящие от стрелки к
глазу наблюдателя и несущие информацию о
результате измерения. Сделав ещё один шаг, можно
отнести к измеряемой системе глаз наблюдателя,
затем также нерв, несущий информацию от глаза к
мозгу, затем зрительную часть коры головного
мозга, и т.д. Таким образом, граница («Heisenberg’s cut»)
между измеряемой системой и тем, что мы
уславливаемся называть прибором, по существу,
произвольна.
При любом выборе этой границы
измеряемая система после измерения находится в
одном из альтернативных состояний (в
использованном выше примере это состояние с
номером 1 или состояние с номером 2) и
характеризуется распределением вероятностей по
этим альтернативам (в этом примере —
соответственно |c1|2 и |c2|2).
Множество альтернатив и вероятностное
распределение на этом множестве не зависит от
проведения границы между измеряемой системой и
прибором. Важно, что выбор границы не влияет ни на
рассуждения, проводимые при расчётах, ни на сами
расчёты. Ни при каком выборе границы не возникает
никаких парадоксов и концептуальных проблем,
поскольку мы: 1) рассматриваем всё множество
альтернативных результатов измерения и 2)
миримся с вероятностным характером
предсказаний.
Когда же возникают парадоксы? Только
тогда, когда мы начинаем говорить о том, что видит
(сознаёт) наблюдатель. И именно при таком
описании измерения, включающем сознание
наблюдателя, возникает качественное изменение: 1)
наблюдатель видит (сознаёт) лишь один результат
измерения и 2) когда он видит этот результат, уже
нет смысла говорить о вероятностях, потому что
событие измерения и выбор результата измерения
совершилось.
Это наводит на мысль, которая в той или
иной форме высказывалась большинством авторов,
обсуждавших концептуальные проблемы квантовой
механики: эти проблемы непосредственно связаны с
сознанием наблюдателя, т.е. с субъективным
аспектом измерения. А это, в свою очередь,
означает, что трудно надеяться решить
концептуальные проблемы (разрешить парадоксы)
квантовой механики, если не включить сознание
наблюдателя непосредственно в описание
квантового измерения4. Именно этой линии мы
будем придерживаться, а в качестве инструмента
для этого выберем многомировую интерпретацию
квантовой механики, предложенную Эвереттом.
________________________
1 Здесь c1 и c2 –
комплексные числа, удовлетворяющие условию |c1|2
+ |c2|2 = 1, а в остальном –
произвольные.
2 E.P.Wigner. Remarks on the mind-body question, in L.G. Good,
editor. The Scientist Speculates, p. 284–302, London, Heinemann, 1961.
3 В данном случае система  (измеряемая) находится в
состоянии
(измеряемая) находится в
состоянии  1,
а система
1,
а система  (прибор)
в состоянии
(прибор)
в состоянии  1
или, альтернативно, система
1
или, альтернативно, система  в состоянии
в состоянии  2, а система
2, а система  – в состоянии
– в состоянии  2.
2.
4 С другой стороны, при желании можно
вообще не ставить концептуальные проблемы,
исключив из теории измерений субъективный
элемент (мы уже говорили об этом, но это важное
обстоятельство следует подчеркнуть).
Продолжение в № 22