Продолжение. См. № 2, 4, 6, 8/06

Проф. М.Б.МЕНСКИЙ,
ФИАН им. П.Н.Лебедева, г. Москва
mensky@lebedev.ru

Странности квантового мира и тайна сознания

ГЛ. 1. История создания квантовой механики (продолжение)

1.4. Частица и волна. Корпускулярно-волновой дуализм (де Бройль, 1923)

Одно из самых поразительных отличий квантовой механики – это провозглашаемый ею корпускулярно-волновой дуализм. Этим термином обозначается то обстоятельство, что фундаментальные материальные объекты, называемые элементарными частицами, похожи одновременно и на волну, и на точечную частицу (корпускулу). Точнее, они обладают и волновыми, и корпускулярными свойствами, проявляя те или другие в зависимости от того, какие измерения над ними производятся. Странная двойственная природа квантовых объектов обнаруживала себя с самого момента возникновения квантовой механики и была одним из основных психологических препятствий, которые приходилось преодолевать создателям новой науки.

Макс Планк ещё в 1900 г. вынужден был ввести минимальные порции (кванты) электромагнитного поля энергией E = h/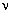, т.е. своего рода «электромагнитные частицы». Однако долгие годы он не мог поверить в их реальность, предпочитая думать о них как об элементах искусственного математического приёма. Следующий шаг в 1905 г. сделал Эйнштейн, который, объясняя фотоэффект, рассуждал о квантах электромагнитного поля как о неделимых порциях, которые могут поглощаться лишь целиком, как элементарные частицы (такие, как электрон). Так были выявлены корпускулярные свойства электромагнитного поля. Поскольку волновые его свойства не подлежали сомнению, фактически приходилось признать двойственную природу этого поля.

В 1923–1924 гг. Луи де Бройль непосредственно подошёл к идее всеобщего корпускулярно-волнового дуализма. Он распространил идею Эйнштейна о двойственной природе электромагнитного поля на вещество. В ряде статей и в своей диссертации де Бройль предположил, что любые материальные частицы (например электрон) обладают волновыми свойствами. Частице с энергией E и импульсом6 p де Бройль сопоставил волну частотой 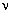= E/h длиной волны 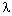= h/p.

Из этого предположения следовало, что все материальные частицы должны в определённых условиях7 вести себя так же, как ведут себя волны, т.е. обнаруживать явления интерференции (когда волны, имеющие противоположные фазы, гасят друг друга, а при совпадении фаз – взаимно усиливаются) и дифракции (когда они огибают непрозрачные препятствия).

Волновые свойства электронов были экспериментально обнаружены Джорджем Томсоном уже в 1927 г. Он наблюдал дифракцию электронов при прохождении их через тонкую золотую фольгу. На экране, который фиксировал прошедшие электроны, обнаруживалась картина дифракционных колец, аналогичная той, что бывает при дифракции волн. Зависимость длины волны электрона от его импульса (т.е. от скорости) совпала с предсказанной де Бройлем.

Ещё раньше, в 1925 г., волновые свойства электронов наблюдал американский физик Клинтон Дэвиссон, который в то время не знал теории де Бройля и потому не мог объяснить свои наблюдения. Таким образом, предположение де Бройля было блестяще подтверждено, и в 1929 г. он получил за свои работы Нобелевскую премию. Вместе с гипотезой Эйнштейна о реальности фотонов теория де Бройля давала симметричную картину. То, что в классической физике представлялось волнами (например свет), как оказалось, обладает свойствами частиц (корпускул), и наоборот: то, что казалось частицами, обнаруживало волновые свойства. Выяснилось, что корпускулярные и волновые свойства неотделимы, они сосуществуют друг с другом. В квантовой механике в отличие от классической нет непроходимой пропасти между волной и частицей. Напротив, любой фундаментальный материальный объект обладает одновременно как волновыми, так и корпускулярными свойствами. Другими словами, вся материя обладает корпускулярно-волновым дуализмом.

Пожалуй, легче примириться с тем, что электромагнитное (да и любое другое) поле состоит из порций, квантов. Гораздо труднее представить себе, что возможна дифракция или интерференция, скажем, электронов. Наиболее яркой иллюстрацией интерференции электронов является двухщелевой эксперимент, который состоит в следующем.

Между источником электронов и сцинтилляционным экраном, на котором они детектируются (или фотоплёнкой), ставится непрозрачный экран с двумя щелями, расстояние между которыми должно быть меньше длины волны электрона 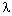= h/p. Тогда на экране образуется интерференционная картина из перемежающихся светлых и тёмных полос (т.е. полос, куда попадает много электронов, и полос, куда их попадает мало). Это значит, что в некоторых точках экрана (фотоплёнки) вероятность обнаружить электрон увеличивается, а в других – уменьшается.

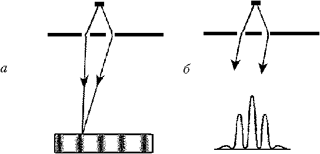
Двухщелевой эксперимент. Электрон, пролетающий через непрозрачный экран с двумя щелями, обнаруживает волновые свойства. При его детектировании возникают интерференционные полосы: направления, в которых электрон обнаруживается с большой вероятностью, чередуются с теми, в которых вероятность мала: а) фотоплёнка засвечивается там, где пролетают электроны; б) зависимость вероятности детектирования электрона от угла (эта зависимость соответствует волновой функции электрона в импульсном представлении)

Легко понять, почему интерференционная картина должна наблюдаться, когда через щели проходит плоская волна. Каждая из щелей становится как бы источником волн, расходящихся во всех направлениях, и в каждую точку экрана (фотоплёнки) приходят две волны, которые там складываются. Они усиливают друг друга, если расстояния от точки наблюдения до щелей одинаковы или различаются на целое число длин волн (в такую точку обе волны приходят с одной и той же фазой), или гасят друг друга, приходя в такую точку в противофазе, если расстояния отличаются на половину длины волны или величину, в нечётное число раз большую. В результате на экране будут чередоваться полосы, в которых амплитуда волны велика, с полосами, где она мала. Это и есть явление интерференции.

Однако, если для волн причина возникающей интерференции ясна, то интерференция электронов кажется неожиданной и странной. По существу, она представляет собой экспериментальное доказательство того, что электроны (да и все вообще материальные частицы) обладают волновыми свойствами.

Странность явления, наблюдаемого в двухщелевом эксперименте, усугубляется тем, что интерференционная картина наблюдается даже в том случае, если поток электронов настолько слаб, что одновременно через щели проходит лишь один электрон. Казалось бы, один электрон может пройти либо через первую, либо через вторую щель, но не через обе. Однако, если это действительно так, то интерференция не может возникнуть. Тот факт, что она всё же возникает, означает, что даже один-единственный электрон проходит сразу через обе щели, и при этом его распространение описывается некоторой волной, полем.

Именно такие соображения в 1926 г. привели Шрёдингера к понятию волновой функции – понятию, до сих пор остающемуся ключевым для квантовой механики.

1.5. Матричная (Гейзенберг, 1925) и волновая (Шрёдингер, 1926) механика

Переход от постулатов Бора к последовательной и точно сформулированной квантовой механике был трудным и совершился в два этапа, которые связаны с именами Гейзенберга и Шрёдингера.

Сначала, в 1925 г., Вернер Гейзенберг предложил матричную форму квантовой механики, в которой наблюдаемые величины (такие, как координата и импульс) представлялись не числами, а матрицами, т.е. квадратными таблицами чисел (строки и столбцы матриц нумеровались частотами, характерными для атома)8. Матрицы, как и числа, можно перемножать, но результат умножения зависит в этом случае от порядка сомножителей. Поэтому умножение наблюдаемых зависит от порядка, в котором они перемножаются. Для двух наблюдаемых, 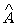и 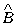, выражение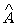 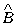отличается от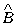 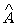выражения . 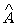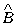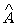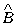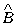Неперестановочность, или некоммутативность, наблюдаемых количественно характеризуется выражением [,] = – 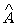, которое называется коммутатором этих наблюдаемых9. Так, коммутатор наблюдаемой положения (координаты) 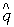и наблюдаемой импульса 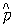равен [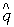, ] = i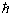, где i – мнимая единица10.

Введение Гейзенбергом некоммутирующих (неперестановочных) наблюдаемых было очень важным шагом. После него коммутатор стал одним из ключевых инструментов в квантовой механике. Впоследствии Гейзенберг показал, что некоммутативность наблюдаемых ведёт к тому, что они не могут быть известны точно, т.е. к тому, что неопределённости, с которыми известны наблюдаемые, подчиняются соотношению неопределённостей и поэтому должны быть отличны от нуля. Но сразу после создания матричной механики он применил её к объяснению спектров атомов – и это ему удалось. Квантовая механика наконец «вышла из пелёнок», получив адекватную и универсальную формулировку, заменившую искусственные конструкции типа постулатов квантования Бора. В 1932 г. Вернер Гейзенберг получил за эту работу Нобелевскую премию.

Параллельно с матричной формой квантовой механики развивалась и другая её форма, волновая. Отправным пунктом была идея де Бройля о том, что движущейся частице с энергией E и импульсом p следует сопоставить волну частоты 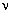= E/h и длины 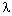= h/p. В 1926 г. Эрвин Шрёдингер довёл эту идею до логического совершенства, сформулировав свою волновую механику. В ней состояние квантовой системы представлялось функцией от координат (волновой функцией) 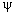(q), а изменение состояния с течением времени описывалось дифференциальным уравнением, впоследствии названным уравнением Шрёдингера. Наблюдаемые величины в волновой механике так же, как в матричной, не коммутировали. Но теперь вместо матриц они выражались операторами, в которых фигурировали производные от волновой функции.

Был некоторый период замешательства, вызванный существованием двух форм механики, применимых к одному и тому же объекту (атому). Для решения конкретных задач можно было пользоваться любой из этих двух форм. Опыт показывал, что они всегда вели к одинаковым выводам. В 1932 г. Джон фон Нейман показал, что эти две физические теории математически эквивалентны. Волновая механика Шрёдингера оказалась удобнее, и в настоящее время для представления состояний квантовых систем и наблюдаемых величин физики используют, как правило, именно язык волновых функций и действующих на эти функции дифференциальных операторов.

Очень важным шагом в понимании роли волновой функции была их вероятностная интерпретация, предложенная в 1926 г. Максом Борном. Волновая функция 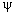(q), введённая Шрёдингером, есть функция координат системы, а значения этой функции – комплексные числа. Борн впервые понял, что квадрат модуля волновой функции |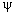(q)|2 в точке q есть плотность вероятности того, что координата имеет значение q. Это значит, что величина |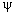(q)|2dq равна вероятности того, что координата лежит в интервале [q, q + dq] (см. рис. а). С большой вероятностью система имеет координату в той области, в которой её волновая функция заметно отличается от нуля. Ширина этой области называется неопределённостью координаты и обозначается q.

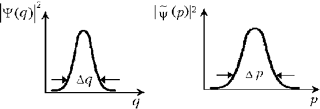
Вероятностная интерпретация волновой функции: а) в координатном представлении: |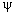(q)|2 – плотность вероятности нахождения частицы в точке q. С большой вероятностью частица находится в области размером q (неопределённость координаты); б) в импульсном представлении: 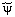|(р)|2 – плотность вероятности того, что частица имеет импульс p. С большой вероятностью импульс частицы принадлежит области размером p (неопределённость импульса)

После работы Борна стало ясно, что волновая функция – это «волна вероятности», и явление интерференции непосредственно следовало из уравнения Шрёдингера. За вероятностную интерпретацию волновой функции Борну в 1954 г. была присуждена Нобелевская премия.

Введение волновой функции существенно изменило представление о том, как ведут себя квантовые частицы, по сравнению с тем, что давали постулаты квантования, введённые Бором. Например, в атоме водорода электрон, согласно постулатам Бора, вращается вокруг положительного ядра (протона) по одной из устойчивых орбит (которые удовлетворяют условию квантования и соответствуют определённой энергии атома En). На самом же деле в атоме, имеющем энергию En, состояние электрона описывается волновой функцией 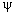n(x, y, z), которая отлична от нуля в некоторой трёхмерной области (а не только на одной кривой – орбите). В частности, в основном состоянии атома водорода (имеющем минимальную энергию E1) волновая функция электрона сферически симметрична. Приближённо можно считать, что эта функция отлична от нуля внутри сферы с центром в ядре атома и с радиусом, равным боровскому радиусу a0 = 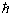2/(me2). Значит, неопределённость каждой из трёх координат электрона (x, y, z) в этом состоянии приблизительно равна a0.

Математический формализм квантовой механики, использующий волновые функции, остался наиболее употребительным до сих пор. В 1926–1927 гг. Поль Дирак разработал теорию преобразований, позволявшую переходить от координатного представления волновой функции 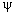(q) к импульсному представлению 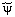(p) или к представлению, связанному с любой другой наблюдаемой11. В 1933 г. Шрёдингер и Дирак были удостоены Нобелевской премии за создание формализма волновых функций, важнейшего математического инструмента в квантовой механике.

Волновая функция в координатном представлении позволяет наглядно представить свойства состояния системы по отношению к координате (или, в общем случае, координатам) этой системы. Переход к другому представлению делает наглядными свойства того же состояния по отношению к другой наблюдаемой.

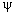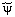Как уже говорилось, величина |(q)|2 (квадрат модуля волновой функции в координатном представлении) интерпретируется как плотность вероятности того, что система имеет координату q. Аналогично интерпретируется и квадрат модуля волновой функции в импульсном представлении, |(р)|2
(см. рис. б). Именно, величина |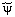(р)|2 есть плотность вероятности того, что система имеет импульс p. Значит, с большой вероятностью импульс системы лежит в области, где волновая функция в импульсном представлении (р) не слишком мала. Ширина этой области p называется неопределённостью импульса12. Оказывается, что неопределённости координат и импульсов квантовой системы не могут быть сколь угодно малыми. Они ограничены принципом неопределённости.

1.6. Особенности квантовых измерений

Измерения, проводимые в квантовой системе, принципиально отличаются от измерений в классической системе. Это отличие было одним из самых трудных пунктов в период становления квантовой механики и обсуждалось с самых разных точек зрения. Существенное прояснение вопроса возникло после открытия Гейзенбергом принципа неопределённости и затем после формулировки Бором принципа дополнительности. Математически корректная формулировка измерения была введена фон Нейманом в форме постулата редукции. Таким образом, к 1932 г. вопрос о квантовых измерениях был в достаточной мере прояснён. На этом мы кратко остановимся в этом разделе.

И всё же даже после этого и вплоть до нашего времени остаются нерешёнными принципиальные вопросы по поводу того, что происходит при измерении квантовой системы. Эти вопросы, ведущие к очень важным выводам, мы будем подробно обсуждать позднее.

1.6.1. Принцип неопределённости (Гейзенберг, 1927). Принцип неопределённости был сформулирован Вернером Гейзенбергом в 1927 г. под сильным влиянием долгих и трудных дискуссий с Бором. Это стало одним из самых важных шагов в понимании той специфики, которой квантовые системы отличаются от классических. Согласно принципу неопределённости, в любом состоянии одномерной системы неопределённость координаты q и неопределённость импульса p удовлетворяют неравенству13 q . 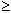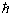p /2.

Это неравенство называется соотношением неопределённостей Гейзенберга, или принципом неопределённости. Оно в чрезвычайно яркой форме выражает одно из основных отличий квантовой механики от классической. Это неравенство применяется чрезвычайно широко, во-первых, для того, чтобы понять поведение той или иной квантовой системы, во-вторых, для грубых оценок некоторых параметров. Пример такой оценки, основанной на соотношении неопределённостей, имеется, например, в начале раздела «Искусственные атомы» (см. № 2/06. – Ред.), где показано, что характерная частота излучения атома обратно пропорциональна квадрату его размера.

Обсудим принцип неопределённости более детально. В классической физике и координата, и импульс точечной частицы имеют определённое значение, т.е. неопределённости и координаты, и импульса равны нулю. Конечно, наблюдаемые всегда известны экспериментатору с некоторыми погрешностями. Однако эти погрешности – всего лишь мера незнания. В принципе, произведя достаточно точные измерения, экспериментатор может сделать погрешности сколь угодно малыми.

В квантовой механике этого сделать нельзя. Даже если состояние частицы известно абсолютно точно (т.е. абсолютно точно известна её волновая функция), неопределённости координаты q и импульса p (ширины координатного и импульсного представлений волновой функции) не равны нулю. Они приобретают в квантовой механике другой статус. Это уже не мера незнания, а характеристики состояния. Произведение q . p ни в каком состоянии не может быть меньше14, чем 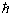/2.

Чтобы проверить соотношение неопределённостей, нужно произвести большое количество очень точных измерений координаты в одном и том же состоянии частицы (которое перед каждым измерением восстанавливается) и выяснить, какой разброс будет наблюдаться в результатах измерений. Затем в том же самом состоянии следует много раз с большой точностью измерить импульс (каждый раз перед измерением приводя частицу в исходное состояние) и найти разброс значений импульса в этой серии измерений. Произведение полученных таким образом величин (Разброс Значений Координаты 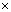Разброс Значений Импульса) будет равен или больше, чем 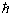/2, где 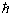= 1,05 . 10–27 эрг . с. Эксперимент всегда подтверждает эту закономерность.

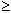
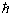Чаще говорят о проверке соотношения неопределённостей в одном измерении, проведённом с конечным разрешением. Например, если измерить координату с разрешением q, то импульс должен получить неопределённость р /(2q). Эту закономерность иллюстрируют обычно мысленным экспериментом, в котором координата измеряется при помощи микроскопа (так называемый микроскоп Гейзенберга), а неопределённость импульса возникает в силу специфических свойств фотонов, которые падают на измеряемый объект во время измерения. Разберёмся в этом более детально.

_____________________

Печатается выборочно и в сокращении по книге М.Б.Менского «Человек и квантовый мир (странности квантового мира и тайна сознания)» (Фрязино: Век 2, 2005; vek-2@mail.ru , http://www.vek2.nm.ru).

6 Импульс, или момент оличества движения, частицы массы m выражается через её скорость формулой p = m.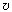

7А именно – когда характерные масштабы, характеризующие среду, через которую распространяются частицы, меньше или порядка 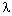= h/p.

8 Гейзенберг, не знавший теории матриц, не подозревал, что в его вычислениях фактически фигурируют именно эти математические объекты. Первым это понял Макс Борн, который вместе с Паскуалем Йорданом сформулировал схему, предложенную Гейзенбергом, в терминах матриц, придав ей более стройный вид.

9 В квантовой механике некоммутирующие наблюдаемые (матрицы или, в более общем случае, операторы), в отличие от обычных числовых переменных, обычно обозначаются буквами с «крышкой», хотя это правило не всегда соблюдается.

10 Мнимая единица появляется не случайно: комплексные и, в частности, мнимые числа – один из основных элементов математического аппарата квантовой механики.

11 Волновые функции в координатном и импульсном представлениях связаны друг с другом преобразованием Фурье.

12 Более точно, q и p – это среднеквадратичные отклонения координаты и импульса от их среднего значения, т.е. 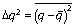и 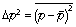, где обозначено 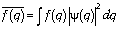и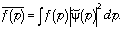

13 Одномерной называется система, которая описывается лишь одной координатой, например электрон, движущийся вдоль заданной прямой. Если система описывается несколькими координатами q1, q2, ... , qn, то каждой из них соответствует свой импульс p1, p2, ... , pn, и для каждой пары qi, pi выполняется точно такое же неравенство.

14 В качестве предельного случая в квантовой механике рассматривают состояния с точно известной координатой, т.е. с нулевой неопределённостью координаты, q = 0. Но неопределённость импульса в таком состоянии бесконечна, p = 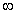. Наоборот, если точно известен импульс, p = 0, то q = .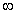

Продолжение в № 12

.  .