Продолжение. См. № 2/06
Проф. М.Б.МЕНСКИЙ,
ФИАН им. П.Н.Лебедева, г. Москва
mensky@lebedev.ru
Странности квантового мира и тайна
сознания
Гл. 2. Некоторые
приложения квантовой механики (продолжение)
2.3. Полупроводниковые
структуры и нанотехнология (продолжение)
Важным направлением в
нанотехнологии оказалось создание углеродных
нанотрубок. Нанотрубка представляет собой
гигантскую молекулу, состоящую из огромного
числа (сотен тысяч и даже миллионов) атомов
углерода.
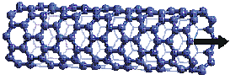
Атомы углерода расположены на
поверхности трубки в вершинах правильных
шестиугольников. Концы трубки закрыты с помощью
шести правильных пятиугольников. Диаметр такой
трубки – около 1 нм, а длина может достигать
нескольких десятков микрометров. Если некоторые
шестиугольники на поверхности трубки заменять
на пятиугольники (тем самым сознательно вводя
«дефекты»), то можно определённым образом
изгибать такие трубки.
Межатомные связи, которые
соединяют атомы углерода друг с другом,
настолько сильны, что бездефектная углеродная
трубка на два порядка прочнее стальной проволоки
того же диаметра. В то же время она в четыре раза
легче. Поэтому на основе таких трубок можно
создавать уникальные прочные и лёгкие
конструкции, которые невозможно изготовить из
обычных материалов.
Конечно, мечтой
исследователей является создание очень длинных
углеродных трубок (теоретически они могут иметь
любую длину). Это открывает фантастические
возможности. Характерным примером является
проект «космического лифта». Это лента длиной в
100 000 км, которая одним концом закреплена на
поверхности Земли. Другой конец оказывается в
космосе, причём вся лента поддерживается в
поднятом положении центробежными силами,
возникающими в результате вращения Земли. Такой
«лифт» позволял бы поднимать в космос грузы с
гораздо меньшей затратой энергии: если на
начальном участке пути грузу нужно сообщить
некоторую скорость, то на конечном этапе
скорость будет увеличиваться за счёт
центробежной силы.
Кроме высокой прочности
длинные нанотрубки должны иметь очень высокую
электрическую проводимость. Предполагается, что
электрические кабели, сделанные из нанотрубок,
при комнатной температуре будут иметь
электрическое сопротивление, которое на два
порядка меньше сопротивления медных кабелей.
Есть, конечно, и другие возможности для
приложения этих удивительных молекул, например,
для конструирования плоских акустических систем
и дисплеев.
Большие технологические
возможности, которые уже сейчас находят
применения, предоставляют так называемые нанокластеры,
т.е. частицы, содержащие от десятков до тысяч
атомов. Из нанокластеров можно целенаправленно
конструировать новые материалы с заранее
заданными свойствами, недостижимыми для обычных
материалов. Можно создать, например, магнитные
кластеры, обладающие собственным магнитным
моментом. Из полученных с помощью таких
кластеров материалов можно создавать магнитную
память нового поколения. Плотность записи при
этом будет достигать 10 ГБ/см2.
Из наноматериалов в принципе
могут создаваться всевозможные наноустройства,
т.е. технические устройства размером в
нанодиапазоне (нанодвигатели, наноманипуляторы,
элементы механизмов нанороботов). Если
большинство такого рода проектов пока остаются
лишь мечтами (хотя в принципе кажутся
возможными), то многочисленные применения
нанотехнологии в медицине и молекулярной
биологии близки к реализации или уже реализованы
в лаборатории. Ведь с помощью наноманипуляторов
можно создавать причудливые конструкции,
включающие как раз те молекулы и макромолекулы,
которые нужны экспериментатору.
Следует заметить, что, как и
всякая эффективная технология, нанотехнология
несёт с собой угрозы, которые трудно заранее
полностью оценить.
2.4. Квантовая информатика
В последние десятилетия ХХ в.
появился ещё один класс приложений квантовой
механики – квантовая информатика. Первая
работа, в которой высказывалась идея квантового
компьютера, была опубликована Р.Фейнманом.
Первые серьёзные разработки по квантовой
информатике связаны с именем Ч.Беннета.
Основными направлениями в квантовой информатике
являются квантовая криптография, квантовый
компьютинг и квантовая телепортация, которые мы
здесь кратко охарактеризуем (интересующиеся
могут найти более детальные, но математически
более сложные сведения о них в самой книге).
Квантовая криптография. Тот
факт, что в классической системе можно
производить измерения, не нарушая её состояния,
означает, что всегда возможен
несанкционированный доступ к такой системе и,
значит, утечка информации. Например, если
некоторое сообщение пересылается по линии связи,
то можно подключиться к этой линии и подслушать
сообщение. При этом всегда можно произвести
подключение таким образом, что само пересылаемое
сообщение никак не изменится и получатель не
будет иметь никакой возможности судить о том,
произошло ли подслушивание. В квантовой механике
дело обстоит совершенно иначе. Любое измерение
квантовой системы неизбежно сопровождается
изменением состояния этой системы. Это позволяет
создавать такие линии связи, что пересылаемые
через них сообщения защищены от подслушивания.
Если говорить точнее, само подслушивание
предотвратить невозможно, однако если
подслушивание произошло, то пересылаемое по
линии сообщение обязательно в чём-то изменится, и
по этим изменениям получатель имеет возможность
обнаружить, что произошло подслушивание и
содержание данного сообщения известно третьей
стороне. Технология квантовой криптографии не
только теоретически обоснована, но и
экспериментально реализована.
Любую информацию можно
представить как длинное двоичное число,
состоящее из нулей и единиц. Поэтому прежде всего
нужен способ записывать каждую из этих двух цифр
(0 и 1) как одно из двух возможных состояний
некоторой квантовой системы. Проще всего в
качестве такой системы взять фотон. В этом случае
цифры 0 и 1 соответствуют одной из двух
поляризаций фотона. Обозначим соответствующие
состояния фотона через 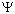 0 и
0 и 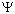 1.
Отправитель сообщения с помощью кодирующего
устройства вырабатывает множество фотонов и
переводит каждый из них, один за другим, либо в
состояние
1.
Отправитель сообщения с помощью кодирующего
устройства вырабатывает множество фотонов и
переводит каждый из них, один за другим, либо в
состояние 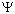 0,
либо в состояние
0,
либо в состояние 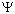 1.
Эта серия фотонов пересылается по световоду к
получателю, где производится измерение
поляризации фотонов, что позволяет расшифровать
сообщение.
1.
Эта серия фотонов пересылается по световоду к
получателю, где производится измерение
поляризации фотонов, что позволяет расшифровать
сообщение.
Если кто-то подключится к
световоду и попытается измерить поляризацию
пересылаемых фотонов, чтобы перехватить
сообщение, то состояния фотонов обязательно (в
силу законов квантовой механики) изменятся.
Протокол, согласно которому отправитель и
получатель производят все операции,
разрабатывается таким образом, чтобы получатель
мог не только расшифровать посланное ему
сообщение, но и убедиться, что полученные им
фотоны не подверглись измерению во время
пересылки, т.е. что не было никакого
подслушивания. И хотя всегда есть некоторая
вероятность того, что подслушивание не будет
обнаружено, за счёт усложнения протокола
кодирования и декодирования она может быть
сделана сколь угодно малой.
Принципиальное отличие
квантовой криптографии от систем, опирающихся
лишь на классическую физику, состоит в том, что
защита от несанкционированного доступа к линии
связи обеспечивается в данном случае законами
природы. Нарушить эти законы и преодолеть защиту
невозможно ни при каких обстоятельствах.
Экспериментальные квантовые
каналы пересылки информации уже сейчас
достигают нескольких десятков километров. Один
такой экспериментальный криптографический
канал проложен по дну Женевского озера. Более
короткие квантово-криптографические линии уже
используются практически. Простейшие из них
поступили на рынок.
Действительно ли квантовая
криптография защищает секреты пользователей?
Какое значение имеет, знает получивший
информацию о том, что информация уже перехвачена
«противником», или нет? Продемонстрируем разницу
на примере двух возможных ситуаций.
Первая относится к случаю,
когда требуется сохранить секретность большей
части пересылаемой информации, однако допустимо,
чтобы небольшая её часть оказалась
рассекреченной. Например, с помощью
квантово-криптографической линии происходит
телефонный разговор. Предположим, что кто-то
сумел подключиться к линии и начал подслушивать.
На то, чтобы обнаружить подслушивание, требуется
некоторое время. Значит, через некоторое время
после начала подслушивания лица,
разговаривающие по секретной линии, получают
предупреждающий сигнал и сразу же прекращают
разговор, после чего принимают меры для
обнаружения и ликвидации подключения.
Если время, когда
подслушивание происходило, но ещё не было
обнаружено, не слишком велико, то за это время
никакой существенной информации «противник» не
получит. Это время можно сделать таким, что его
достаточно лишь для произнесения одного слова.
Можно сделать его ещё короче, и тогда оно вместит
лишь часть слова. В этом случае подслушивание не
принесёт никакого ущерба.
Иная ситуация имеет место в
том случае, если сообщение, пересылаемое по
линии, настолько важно, что нельзя допустить
рассекречивания никакой, даже самой малой его
части. Для этого нужно пересылать по
квантово-криптографической линии не саму
содержательную информацию, а лишь секретное
кодовое слово.
Обычная практика секретной
переписки, используемая спецслужбами во всем
мире, состоит в том, что сами секретные сообщения
пересылаются по открытым каналам, которые может
прослушать кто угодно (например, по радио), однако
в зашифрованном виде. Если «противник»,
перехвативший такое сообщение, не обладает кодом
для его дешифровки, то он увидит лишь длинный ряд
цифр, которые не дадут ему ровно никакой
информации. Скрывающееся за этими цифрами
зашифрованное сообщение останется для него
тайной. Правда, он может применить специальные
методы дешифровки, которые позволяют
расшифровать любое достаточно длинное сообщение
(тем более, что сам метод кодирования применяется
многократно и поэтому известен «противнику»).
Однако на дешифровку достаточно сложного кода,
даже с применением мощных компьютеров, требуется
значительное время, и за это время сообщение
успевает устареть*. (* При необходимости код можно
сделать настолько сложным, что для декодирования
с помощью обычных классических компьютеров не
хватит даже времени, сопоставимого со временем
существования Вселенной. В этом случае помочь в
дешифровке может лишь достаточно мощный
квантовый компьютер, которого пока не
существует. Это одна из причин, почему на
разработку квантовых компьютеров тратятся
большие усилия и деньги.) Что же касается
адресата, которому направлено сообщение, то он
производит расшифровку очень быстро, т.к. знает
не только метод кодирования, но и кодовое слово,
являющееся ключом к шифру. Поэтому, если
периодически менять кодовое слово, секретность
сообщений обеспечивается.
Задача сводится, таким
образом, к тому, чтобы время от времени
пересылать само кодовое слово (практически –
длинное двоичное число) так, чтобы было
достоверно известно, что при пересылке не
произошла утечка информации. В этом уже может
помочь квантовая криптография. Кодовое слово при
помощи специального протокола записывается в
состояниях пересылаемых по световоду фотонов.
Этот протокол устроен таким образом, чтобы
получивший серию фотонов, произведя над ними
соответствующую серию измерений, мог не только
восстановить записанное двоичное число, но и
понять, изменились ли состояния фотонов во время
пересылки, т.е. произошло ли подслушивание. Если
выясняется, что подслушивание произошло, то
получатель сообщает по открытому каналу, что
данное кодовое слово использовать нельзя, и ждёт
присылки другого. Если же он убеждается, что
подслушивания не произошло, кодовое слово
продолжает использоваться для пересылки
содержательных сообщений.
Напомним ещё раз, что
вероятность обнаружения подслушивания зависит
от используемого протокола кодирования, и за
счёт усложнения этого протокола можно сделать
эту вероятность сколь угодно близкой к единице.
Важно, что в рамках данной вероятности
секретность обеспечивается абсолютно. Её
нарушение означало бы нарушение законов
квантовой механики, что в принципе невозможно.
Квантовый компьютинг. В
последние десятилетия предложен, теоретически
разработан и даже реализован (пока лишь на
простейших прототипах) принцип квантового
компьютинга. Он позволяет вместо хорошо всем
знакомых классических компьютеров использовать
квантовые. В чем же преимущества квантовых
компьютеров и на чём основаны эти преимущества?
Довольно широко известно, что квантовые
компьютеры, когда (и если) они достигнут
достаточной мощности, смогут решать такие
вычислительные задачи, которые не под силу
обычным. Это объясняется тем, что в квантовом
компьютере используется квантовый параллелизм.
Суть его можно понять, сравнивая, как хранится
информация в классическом и квантовом
компьютерах.
В обычных компьютерах
информация хранится в форме двоичных чисел, у
которых в каждом разряде стоит либо цифра 0, либо
цифра 1. Каждая из этих цифр хранится в двоичной
ячейке памяти. Таким образом, одна двоичная
ячейка – это физическая система, которая может
находиться в одном из двух устойчивых состояний.
Одно из них соответствует цифре 0, другое – цифре
1. В такой ячейке хранится информация,
соответствующая выбору между двумя вариантами
(цифрами 0 и 1 или, эквивалентно, двумя состояниями
системы). Говорят, что количество информации,
хранящееся в двоичной ячейке, равно 1 биту. В
двух двоичных ячейках хранится 2 бита информации.
Это соответствует выбору между 2-разрядными
двоичными числами 00, 01, 10 и 11. В регистре,
состоящем из N двоичных ячеек, хранится N
битов информации, что соответствует выбору
одного N-разрядного двоичного числа из всех
возможных (всего таких чисел 2N).
Посмотрим теперь, чем
отличается хранение информации в квантовом
компьютере. Сама информация тоже может быть
представлена в форме двоичных чисел, т.е. цепочек
нулей и единиц. Одна цифра двоичного числа
хранится в двоичной ячейке. Эта ячейка
называется кубитом (англ. qubit, сокращённое от quantum
bit, т.е. квантовый бит) и представляет собой
квантовую систему, одно из состояний которой
соответствует цифре 0, а второе – цифре 1.
Обозначим эти состояния 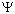 0 и
0 и 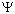 1.
1.
Именно в этом пункте
появляется существенное отличие от
классического компьютера. Дело в том, что для
квантовых систем имеет место так называемый принцип
суперпозиции. Он состоит в следующем. Если
квантовая система может находиться в одном из
двух состояний, скажем, в состоянии 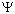 0 и в состоянии
0 и в состоянии 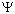 1, то она может также
находиться в целом семействе состояний, которые
строятся как линейные комбинации исходных.
Это значит, что исходные состояния умножаются на
некоторые (комплексные) числа и складываются.
Если выбираются числа c0 и c1,
то получается состояние c0
1, то она может также
находиться в целом семействе состояний, которые
строятся как линейные комбинации исходных.
Это значит, что исходные состояния умножаются на
некоторые (комплексные) числа и складываются.
Если выбираются числа c0 и c1,
то получается состояние c0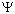 0 + c1
0 + c1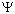 1. Таким образом, с состояниями
можно обращаться как с векторами, т.е. умножать их
на любые числа и складывать. Говорят, что все
возможные состояния образуют векторное
пространство (другой термин – линейное
пространство). Отличие от обычных векторов
состоит лишь в том, что числовые множители могут
быть не только вещественными, но и комплексными
числами, т.е. состояния образуют векторное
пространство над полем комплексных чисел. Нам
не нужна будет эта математика в полном объёме, но
если читатель интересуется, он может
познакомиться с ней ближе (см. книгу).
1. Таким образом, с состояниями
можно обращаться как с векторами, т.е. умножать их
на любые числа и складывать. Говорят, что все
возможные состояния образуют векторное
пространство (другой термин – линейное
пространство). Отличие от обычных векторов
состоит лишь в том, что числовые множители могут
быть не только вещественными, но и комплексными
числами, т.е. состояния образуют векторное
пространство над полем комплексных чисел. Нам
не нужна будет эта математика в полном объёме, но
если читатель интересуется, он может
познакомиться с ней ближе (см. книгу).
Для нас достаточно будет
выбрать простейшие множители c0 = c1=
1. Тогда мы заключаем, что наряду с состояниями 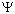 0 и
0 и 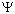 1 кубит может также
находиться в состоянии
1 кубит может также
находиться в состоянии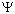 0 +
0 + 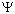 1. Но
это значит, что в одном кубите одновременно
хранятся обе цифры, 0 и 1. Вот это и приводит к
тому, что квантовый компьютер обладает свойством
квантового параллелизма.
1. Но
это значит, что в одном кубите одновременно
хранятся обе цифры, 0 и 1. Вот это и приводит к
тому, что квантовый компьютер обладает свойством
квантового параллелизма.
Итак, в одной двоичной ячейке
квантового компьютера, называемой кубитом,
может храниться не только одна из двух цифр
двоичного счисления, 0 или 1 (как было бы в случае
классического компьютера), но одновременно обе
эти цифры. В двух кубитах могут храниться
одновременно 4 двоичных числа 00, 01, 10 и 11. А если в
некотором регистре квантового компьютера
содержится N кубитов, то в таком регистре
может храниться одновременно 2N
двоичных чисел длины N. И при действии
квантового компьютера одновременно
обрабатываются все эти числа.
Если бы в нашем распоряжении
были только классические компьютеры, каждый из
которых работает с двоичными числами длины N,
то для одновременной обработки 2N таких
чисел было бы необходимо 2N компьютеров.
Если же мы сумели построить квантовый компьютер,
содержащий N кубитов, то один (!) этот
компьютер одновременно обрабатывает все 2N
чисел.
Если, скажем, N = 100, то мы
получаем выигрыш в 2100 раз, что примерно
равно миллиону. А если
N = 1000, то получается выигрыш в 21000 ~ 10300
раз. Именно этим объясняется, почему квантовый
компьютер может (если он будет практически
реализован с достаточно большим N) решать
такие задачи, на которые классическим
компьютерам не хватит времени, сравнимого с
временем существования Вселенной.
Проблема, стоящая перед этой
областью науки, состоит в том, чтобы реализовать
квантовые компьютеры с достаточно большим
числом кубитов. Пока удалось реализовать лишь
образцы с N порядка десяти*. (* Кубиты могут быть реализованы
различными способами. Это могут быть, например,
ионы, подвешенные в магнитной ловушке. Роль
выделенных состояний 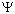 0 и
0 и 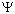 1 играют два уровня энергии иона, тогда
как некоторые другие уровни используются для
управления кубитом. Нахождение в магнитной
ловушке обеспечивает изоляцию иона. Это
необходимо для того, чтобы он работал в квантовом
режиме.) Целью же является реализовать компьютер,
в котором N достигает тысячи или хотя бы ста.
Над этим работают во всем мире огромное число
специалистов, и принципиальных запретов на
построение таких устройств пока не обнаружено.
1 играют два уровня энергии иона, тогда
как некоторые другие уровни используются для
управления кубитом. Нахождение в магнитной
ловушке обеспечивает изоляцию иона. Это
необходимо для того, чтобы он работал в квантовом
режиме.) Целью же является реализовать компьютер,
в котором N достигает тысячи или хотя бы ста.
Над этим работают во всем мире огромное число
специалистов, и принципиальных запретов на
построение таких устройств пока не обнаружено.
Мы видели, что квантовые
компьютеры, которые работали бы с достаточно
длинными двоичными числами, имели бы огромные
преимущества перед классическими. Это
преимущество на практике должно проявляться в
скорости вычислений. Если с ростом длины
двоичных чисел N время вычислений на
классическом компьютере растёт экспоненциально
(TN 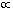 e
e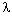 N – c некоторым
числовым множителем
N – c некоторым
числовым множителем 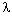 ), то для квантового компьютера этот рост
лишь полиномиальный, т.е. TN
), то для квантового компьютера этот рост
лишь полиномиальный, т.е. TN 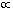 N
N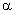 – c некоторым числом
– c некоторым числом 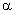 в качестве показателя степени).
При больших N разница между этими двумя
законами роста становится решающей. В результате
некоторые задачи, решение которых на
классическом компьютере заняло бы время,
сравнимое со временем существования Вселенной,
на квантовом компьютере могут быть решены за
разумное время.
в качестве показателя степени).
При больших N разница между этими двумя
законами роста становится решающей. В результате
некоторые задачи, решение которых на
классическом компьютере заняло бы время,
сравнимое со временем существования Вселенной,
на квантовом компьютере могут быть решены за
разумное время.
В отличие от классических,
квантовые компьютеры не универсальны: не для
всяких вычислительных задач существует алгоритм
их решения. До сих пор найдено лишь небольшое
число квантовых алгоритмов. Зато среди них есть
практически очень важные. Наиболее известен
алгоритм Шора, который позволяет решить любую из
двух математически эквивалентных задач: найти
период сложной периодической функции или
разложить на простые множители очень большое
число.
Вторая задача имеет важное
прикладное значение, потому что она используется
в криптографии. Дело в том, что в одной из
криптографических методик для шифровки и
дешифровки секретных посланий используют
большие числа, для которых известны их
разложения на множители. Ясно, что такие числа
получить легко: достаточно перемножить большое
число простых чисел, и мы получим очень большое
число, для которого разложение на простые
множители известно. Получатель закодированного
секретного послания может его декодировать
потому, что в процедуре декодирования
используется разложение на множители длинного
числа, а он знает это разложение. Если бы
противник смог разложить это число на простые
множители, он также смог бы декодировать
послание. Однако для такого разложения требуется
огромное время. Поэтому с практической точки
зрения декодировать такое послание невозможно.
Но если бы в распоряжении противника был
квантовый компьютер (достаточной мощности,
т.е.работающий с достаточно большими числами), то
он мог бы это делать и значит легко мог бы
расшифровывать такого рода послания.
Распространённый в криптографии метод перестал
бы работать. Это один из аргументов, которые
делают важным создание квантового компьютера.
До практической реализации мощных
квантовых компьютеров ещё очень далеко, если
вообще эта цель достижима. Однако уже сейчас
созданные прототипы показывают, что сам принцип
квантового компьютинга справедлив. Ниже мы
вернёмся к этому в связи с совершенно другим, но
не менее интригующим вопросом о работе сознания.
_______________________________
Печатается выборочно и в сокращении по
книге М.Б.Менского «Человек и квантовый мир
(странности квантового мира и тайна сознания)»
(Фрязино: Век2, 2005; vek-2@mail.ru)