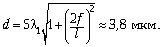Продолжение. См. № 1, 3, 5, 7/06
С.С.ЧЕСНОКОВ, С.Ю.НИКИТИН,
И.П.НИКОЛАЕВ, Н.Б.ПОДЫМОВА,
М.С.ПОЛЯКОВА, проф. В.И.ШМАЛЬГАУЗЕН,
физфак МГУ, г. Москва
sergeychesnokov@mail.ru
Хочу учиться на ВМК!
Задачи, предлагавшиеся на
вступительных экзаменах на факультет
вычислительной математики и кибернетики МГУ им.
М.В.Ломоносова в 2005 г.
IV. ОПТИКА (окончание)
2 На некотором
расстоянии от стеклянного шара находится
точечный источник света, дающий узкий световой
пучок, ось которого проходит через центр шара.
При каких значениях показателя преломления
стекла n изображение источника будет
находиться вне шара независимо от расстояния, на
котором находится источник?
 Решение
Решение
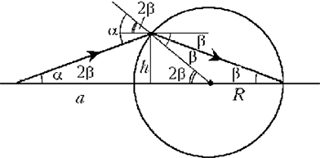
Пусть источник находится на
расстоянии a от поверхности шара. Ход одного
из лучей, испущенных источником, изображён на
рисунке в предположении, что этот луч пересекает
заднюю часть поверхности шара на оптической оси.
В этом случае с учётом малости углов падения и
преломления имеем:
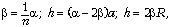
где h – расстояние от точки падения
луча на поверхность шара до его оси, R –
радиус шара. Объединяя эти равенства, находим
показатель преломления n0, при котором
изображение источника располагается на задней
поверхности шара:
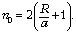
При n < n0 точка
пересечения преломлённых шаром лучей с
оптической осью (изображение источника) выйдет
за пределы шара. При a 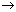
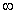 находим, что n0
находим, что n0 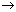 2. Таким образом, для источника, удалённого на
большое расстояние, достигается наименьшее
значение показателя преломления,
удовлетворяющее условию задачи. Следовательно,
изображение источника всегда будет находиться
вне шара при n < 2.
2. Таким образом, для источника, удалённого на
большое расстояние, достигается наименьшее
значение показателя преломления,
удовлетворяющее условию задачи. Следовательно,
изображение источника всегда будет находиться
вне шара при n < 2.
3 Узкий световой
пучок падает на тонкую собирающую линзу
параллельно её главной оптической оси и образует
светлое пятно на экране, параллельном плоскости
линзы и расположенном за ней на расстоянии l.
Когда линзу передвинули на расстояние 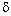 в направлении,
перпендикулярном её главной оптической оси,
центр пятна сместился на величину
в направлении,
перпендикулярном её главной оптической оси,
центр пятна сместился на величину 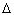 . Найдите фокусное
расстояние линзы f.
. Найдите фокусное
расстояние линзы f.
 Решение
Решение
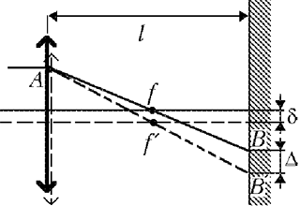
Ход одного из лучей, образующих пучок,
изображён на рисунке для случая, когда l > f.
Сплошные линии соответствуют исходному
положению линзы, штриховые – смещённому. Из
подобия 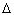 Aff '
и
Aff '
и 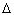 ABB'
следует, что
ABB'
следует, что
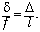
Отсюда 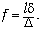 Аналогично рассматривается случай,
когда l < f. Наконец, если перемещение
линзы выходит из плоскости рисунка, то лучи,
преломлённые линзой в исходном и смещённом её
положениях, по-прежнему будут лежать в одной
плоскости, в которой можно рассмотреть такие же
подобные треугольники. Следовательно, связь
между смещениями линзы и светового пятна на
экране во всех случаях имеет один и тот же вид.
Аналогично рассматривается случай,
когда l < f. Наконец, если перемещение
линзы выходит из плоскости рисунка, то лучи,
преломлённые линзой в исходном и смещённом её
положениях, по-прежнему будут лежать в одной
плоскости, в которой можно рассмотреть такие же
подобные треугольники. Следовательно, связь
между смещениями линзы и светового пятна на
экране во всех случаях имеет один и тот же вид. 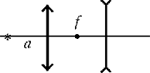
4 Собирающая и
рассеивающая линзы имеют одинаковые по модулю
фокусные расстояния f и расположены так,
что задний фокус собирающей линзы совмещён с
передним фокусом рассеивающей. На каком
расстоянии а от собирающей линзы следует
поместить точечный источник света, чтобы после
рассеивающей линзы получить пучок параллельных
лучей?
Решение 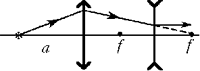
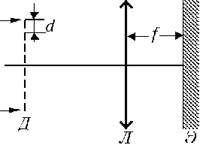
Пучок света после рассеивающей линзы
будет параллельным, если продолжения падающих на
неё лучей пересекаются в её заднем фокусе (см.
рисунок). Для этого изображение источника,
даваемое собирающей линзой, должно
располагаться на расстоянии f позади
рассеивающей линзы, т.е. на расстоянии 3f от
собирающей линзы. Расстояние a, на котором
надо поместить источник света перед собирающей
линзой, можно найти по формуле тонкой линзы:
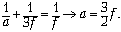
5 С помощью
установки, схема которой показана на рисунке,
наблюдают дифракцию параллельного пучка белого
света на дифракционной решётке Д,
расположенной перпендикулярно оси пучка. При
этом на экране Э, установленном в фокальной
плоскости тонкой собирающей линзы Л, видны
две светлые полосы, вызванные наложением
спектральных компонент с длинами волн 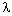 1 = 460 нм и
1 = 460 нм и 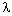 2 = 575 нм. Эти
полосы расположены симметрично относительно
главной оптической оси линзы на расстоянии l =
30 см друг от друга. Найдите минимальный период
решётки dmin, при котором наблюдается эта
картина, если фокусное расстояние линзы f = 20
см.
2 = 575 нм. Эти
полосы расположены симметрично относительно
главной оптической оси линзы на расстоянии l =
30 см друг от друга. Найдите минимальный период
решётки dmin, при котором наблюдается эта
картина, если фокусное расстояние линзы f = 20
см.
Решение 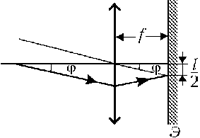
Углы, определяющие направления на
дифракционные максимумы, определяются условием 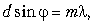
где m = 0, 1, 2, ... . Наложение
спектральных компонент с длинами волн 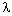 1 и
1 и 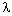 2
происходит, если m1
2
происходит, если m1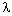 1 = m2
1 = m2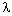 2.
2.
Анализ числовых данных показывает, что
минимальные значения m1 и m2,
при которых выполняется это условие, равны: m1
= 5, m2 = 4. Следовательно,
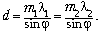
Из рисунка видно, что 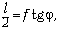 откуда
откуда 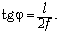
Используя формулу 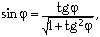 получаем ответ:
получаем ответ: