Продолжение. См. № 1, 3/06

С.С.ЧЕСНОКОВ, С.Ю.НИКИТИН,
И.П.НИКОЛАЕВ, Н.Б.ПОДЫМОВА,
М.С.ПОЛЯКОВА, проф. В.И.ШМАЛЬГАУЗЕН,
физфак МГУ, г. Москва
sergeychesnokov@mail.ru

Хочу учиться на ВМК!

III. Электродинамика (продолжение)

10 Заряженный конденсатор ёмкостью C замыкают на реостат, сопротивление которого плавно изменяется от R₀ до нуля. По какому закону нужно менять во времени сопротивление реостата, чтобы сила тока через него оставалась постоянной вплоть до полной разрядки конденсатора? Сопротивление реостата в начале разрядки равно R₀.

Решение

По закону Ома, ток через резистор равен 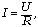где 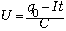– напряжение на конденсаторе в момент времени t, R – сопротивление резистора в этот же момент, q₀ – начальный заряд на конденсаторе. Здесь учтено, что, по условию, ток через резистор постоянен. Используя для тока его значение 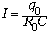  в начальный момент времени, приходим к равенству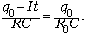

Отсюда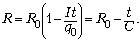

Ответ. 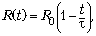  где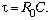

11 Два плоских воздушных конденсатора ёмкостями С₁ = 100 мкФ и С₂ = 200 мкФ соединены последовательно и подключены к источнику с ЭДС 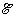= 60 В. Какую работу А совершит источник, если пространство между пластинами конденсатора С₁ заполнить диэлектриком с диэлектрической проницаемостью 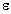= 4?

Решение

Начальный заряд на конденсаторах равен

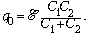
После внесения диэлектрика заряд на конденсаторах станет

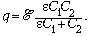
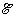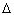Работа источника по переносу заряда q = q – q₀ равна А = • q.

Ответ.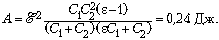

12 Плоский воздушный конденсатор ёмкостью C₀ с квадратными обкладками, сторона каждой из которых равна l, подключён к источнику с ЭДС 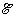. В конденсатор вставляют пластинку диэлектрической проницаемостью 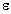, занимающую всё пространство между обкладками, а затем выдвигают её из конденсатора на небольшое расстояние, как показано на рисунке. Какую силу F нужно приложить к пластинке, чтобы удерживать её в таком положении?

Решение

Обозначим через x расстояние, на которое диэлектрическая пластинка выдвинута из конденсатора. Ёмкость конденсатора с частично выдвинутой пластинкой равна

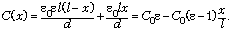
При выдвигании пластинки заряд на конденсаторе изменится на величину

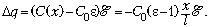
Поскольку заряд на конденсаторе уменьшается, работа источника отрицательна:

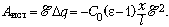
Энергия конденсатора при выдвигании пластинки также уменьшится:

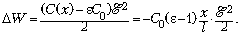
Изменение энергии конденсатора равно сумме работы A силы F и работы источника A_ист: 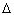W = A + A_ист, откуда

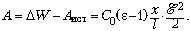
Поскольку A = Fx, ответ имеет вид:

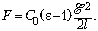
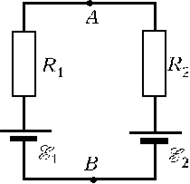
13 В схеме, изображённой на рисунке, напряжение между точками A и B равно U, а сопротивления резисторов R₁ и R₂ неизвестны. Каким будет напряжение V между точками A и B, если поменять местами резисторы R₁ и R₂? ЭДС источников равны 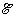₁ и 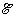₂, внутренними сопротивлениями источников пренебречь.

Решение

Согласно закону Ома для полной цепи, ток в цепи

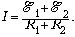
Применяя закон Ома для участка цепи, содержащего ЭДС, имеем:

U = 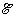₁ – IR₁ (при исходном подключении резисторов);

V = 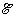₁ – IR₂ (когда резисторы поменяли местами).

Подставив в эти равенства найденную выше силу тока, приведём их к виду:

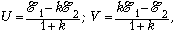где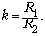

Исключая отсюда k, получаем ответ:

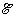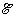V = ₁ – ₂ – U.