Продолжение. См. № 23/05
С.С.ЧЕСНОКОВ,С.Ю.НИКИТИН,
И.П.НИКОЛАЕВ, Н.Б.ПОДЫМОВА,
М.С.ПОЛЯКОВА, проф. В.И.ШМАЛЬГАУЗЕН,
физфак МГУ, г. Москва
sergeychesnokov@mail.ru
Хочу учиться на ВМК!
Задачи, предлагавшиеся на
вступительных экзаменах на факультет
вычислительной математики и кибернетики МГУ им.
М.В.Ломоносова в 2005 г.
I. МЕХАНИКА (окончание)
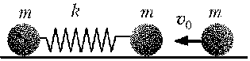
9 Два одинаковых
шарика массой m каждый, связанные пружиной
жёсткостью k и длиной l, лежат неподвижно
на гладком горизонтальном столе. Третий такой же
шарик движется со скоростью 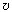 0 по линии, соединяющей центры
шариков, связанных пружиной, и упруго
соударяется с одним из них. Определите
максимальное и минимальное расстояния между
шариками, связанными пружиной, при их дальнейшем
движении. Принять, что
0 по линии, соединяющей центры
шариков, связанных пружиной, и упруго
соударяется с одним из них. Определите
максимальное и минимальное расстояния между
шариками, связанными пружиной, при их дальнейшем
движении. Принять, что 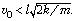 Массой пружины, временем соударения и
трением пренебречь.
Массой пружины, временем соударения и
трением пренебречь.
Решение
Из законов сохранения импульса и
энергии, записанных для упругого соударения
одинаковых по массе шариков, следует, что они при
центральном ударе обмениваются скоростями.
Поэтому после соударения двигавшийся шарик
остановится, а покоившийся приобретёт скорость 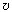 0. При последующем
движении шариков, связанных пружиной, будут
сохраняться импульс и энергия этой системы.
Учитывая, что в моменты времени, когда расстояния
между шариками максимальны или минимальны, их
относительная скорость обращается в нуль, для
этих моментов времени имеем:
0. При последующем
движении шариков, связанных пружиной, будут
сохраняться импульс и энергия этой системы.
Учитывая, что в моменты времени, когда расстояния
между шариками максимальны или минимальны, их
относительная скорость обращается в нуль, для
этих моментов времени имеем:
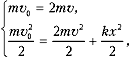
где 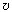 –
скорость шариков, x – удлинение пружины. Из
этих соотношений находим
–
скорость шариков, x – удлинение пружины. Из
этих соотношений находим
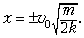
Ответ. 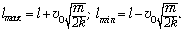
10 Груз массой M
подвешен на пружине. Удерживая груз в положении
равновесия, на него кладут брусок массой m, а
затем отпускают. С какой максимальной силой
брусок будет действовать на груз в процессе
движения? Ускорение свободного падения g.
Сопротивлением воздуха пренебречь.
Решение
Из условия равновесия неподвижно
висящего груза kx0 = Mg следует, что
удлинение пружины при этом равно 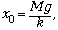 где k – жёсткость
пружины. Совместим начало отсчёта потенциальной
энергии с концом недеформированной пружины.
Учитывая, что при максимальном растяжении
пружины (x = xmax) скорость груза с
бруском обращается в нуль, запишем закон
сохранения энергии:
где k – жёсткость
пружины. Совместим начало отсчёта потенциальной
энергии с концом недеформированной пружины.
Учитывая, что при максимальном растяжении
пружины (x = xmax) скорость груза с
бруском обращается в нуль, запишем закон
сохранения энергии:
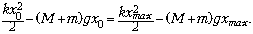
Подставляя сюда x0, находим 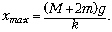
Запишем далее уравнения движения для
груза с бруском и отдельно для бруска:
(M + m)a = (M + m)g – kx; ma =
mg – F.
Отсюда сила, с которой груз действует
на брусок, равна 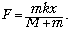
Максимальное значение эта сила
принимает при x = xmax. Объединяя
записанные выражения, получаем окончательно 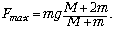
II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
1 Плотность смеси
азота и кислорода при температуре t = 17 °С и
давлении p0 = 105 Па равна 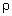 = 1,2 кг/м3. Найдите
концентрации n1 и n2 молекул
азота и кислорода в смеси. Молярная масса азота M1
= 28 г/моль, кислорода M2 = 32 г/моль.
Постоянная Больцмана k = 1,38 · 10–23 Дж/К,
универсальная газовая постоянная R = 8,31
Дж/(моль·К).
= 1,2 кг/м3. Найдите
концентрации n1 и n2 молекул
азота и кислорода в смеси. Молярная масса азота M1
= 28 г/моль, кислорода M2 = 32 г/моль.
Постоянная Больцмана k = 1,38 · 10–23 Дж/К,
универсальная газовая постоянная R = 8,31
Дж/(моль·К).
Решение
Плотность и давление идеального газа
выражаются следующим образом: 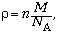 p = nkT, где n –
концентрация молекул, M – молярная масса
газа, k – постоянная Больцмана, NA –
число Авогадро, T – абсолютная температура.
Используя эти выражения, для смеси газов
получаем систему уравнений:
p = nkT, где n –
концентрация молекул, M – молярная масса
газа, k – постоянная Больцмана, NA –
число Авогадро, T – абсолютная температура.
Используя эти выражения, для смеси газов
получаем систему уравнений:
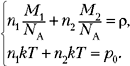
Отсюда, учитывая, что kNA = R,
получаем ответ:
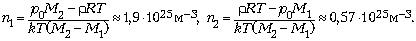
2 Тонкая
сферическая оболочка воздушного шара
изготовлена из однородного материала, масса
единицы площади которого 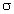 = 1 кг/м2. Шар наполнен гелием при
атмосферном давлении p0 = 105 Па.
Какой минимальный радиус rmin должен
иметь шар, чтобы он начал подниматься?
Температуры гелия и окружающего воздуха
одинаковы и равны t0 = 0 °С. Молярные
массы гелия и воздуха соответственно MHe
= 4 г/моль и Mв = 29 г/моль. Универсальная
газовая постоянная R = 8,31 Дж/(моль · К).
= 1 кг/м2. Шар наполнен гелием при
атмосферном давлении p0 = 105 Па.
Какой минимальный радиус rmin должен
иметь шар, чтобы он начал подниматься?
Температуры гелия и окружающего воздуха
одинаковы и равны t0 = 0 °С. Молярные
массы гелия и воздуха соответственно MHe
= 4 г/моль и Mв = 29 г/моль. Универсальная
газовая постоянная R = 8,31 Дж/(моль · К).
Решение
Шар будет подниматься, если
действующая на него выталкивающая сила превысит
силу тяжести. По закону Архимеда, выталкивающая
сила равна mвg, где mв –
масса воздуха в объёме, занимаемом шаром.
Обозначив через mHe массу гелия,
содержащегося в шаре, а через M – массу
оболочки шара, запишем условие, при котором шар
начнёт подниматься: 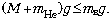
Массы гелия и воздуха, содержащихся в
объёме V, можно найти из уравнений состояния
этих газов:
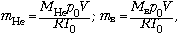
где T0 = t0 + 273 °C, 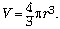 Учитывая, что
масса оболочки шара равна
Учитывая, что
масса оболочки шара равна 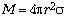 , перепишем условие подъёма шара
в виде
, перепишем условие подъёма шара
в виде
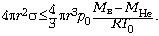
При этом знак равенства достигается
при минимальном радиусе шара.
Окончательно 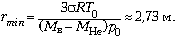
3 Внутри
вертикально расположенного цилиндра, воздух из
которого откачан, находится тонкий массивный
поршень. Под поршень ввели смесь водорода и
гелия, в результате чего поршень поднялся до
середины цилиндра. Поскольку материал, из
которого изготовлен поршень, оказался
проницаемым для гелия, поршень начал медленно
опускаться. Спустя достаточно большое время
поршень занял окончательное положение
равновесия на высоте, составляющей 1/3 высоты
цилиндра. Найдите отношение k масс водорода и
гелия в смеси в первоначальный момент. Молярная
масса водорода M1 = 2 г/моль, молярная
масса гелия M2 =
= 4 г/моль. Температуру считать постоянной.
Решение
Пусть m1 и m2 –
соответственно массы водорода и гелия в смеси, M0
– масса поршня, V – объём цилиндра, S –
площадь сечения поршня, T – температура. Из
условия равновесия поршня и уравнения
начального состояния смеси следует равенство
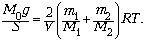
В конечном состоянии, когда диффузия
гелия закончится, концентрация гелия в обеих
частях цилиндра станет одинаковой.
Следовательно, станут равными парциальные
давления гелия снизу и сверху от поршня. Поэтому
давление поршня будет уравновешиваться только
давлением водорода:
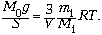
Сопоставляя записанные выражения,
получаем, что 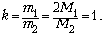 Массы водорода и гелия в смеси были одинаковыми.
Массы водорода и гелия в смеси были одинаковыми.
4 В тепловом
двигателе, рабочим телом которого является
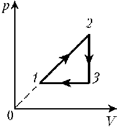
идеальный одноатомный газ, совершается
циклический процесс, изображённый на рисунке.
Максимальный объём газа в этом процессе в n = 3
раза больше минимального объёма. Найдите КПД
двигателя 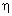 .
.
Решение
Работа газа в циклическом процессе
численно равна площади фигуры, ограниченной
графиком процесса на p, V-диаграмме:
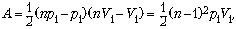
где p1 и V1 –
давление и объём газа в точке 1. Количество
теплоты, полученной газом в данном процессе,
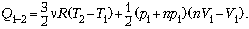
Поскольку 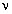 RT1 = p1V1 и
RT1 = p1V1 и 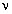 RT2 = n2p1V1,
то Q1–2 = 2p1V1(n2
– 1). КПД цикла
RT2 = n2p1V1,
то Q1–2 = 2p1V1(n2
– 1). КПД цикла 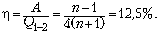
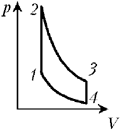
5 В тепловом
двигателе, рабочим телом которого является
идеальный одноатомный газ, совершается
циклический процесс, изображённый на рисунке,
где участок 2–3 – адиабатическое расширение,
а участок 4–1 – адиабатическое сжатие.
Найдите КПД двигателя 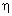 , если известно, что температура газа при
адиабатическом расширении уменьшается в n
раз, а при адиабатическом сжатии увеличивается в n
раз, где n = 1,5.
, если известно, что температура газа при
адиабатическом расширении уменьшается в n
раз, а при адиабатическом сжатии увеличивается в n
раз, где n = 1,5.
Решение
Работа газа за цикл равна
алгебраической сумме количеств теплоты,
которыми газ обменивается с окружающими телами:
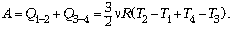
Количество теплоты, полученной газом,
равно
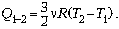
Следовательно, КПД цикла 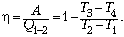
По условию задачи, T2 = nT3;
T1 = nT4.
Ответ.
6 В тепловом
двигателе, рабочим телом которого является один
моль идеального одноатомного газа, совершается
циклический процесс, изображённый на рисунке,
где участок 2–3 – изотермическое расширение.
Найдите работу газа на участке 2 – 3, если КПД
двигателя 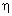 = 20%, а
разность между максимальной и минимальной
температурами газа
= 20%, а
разность между максимальной и минимальной
температурами газа 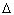 T
= 100 К.
T
= 100 К.
Решение
Работа газа за цикл равна (см. решение
задачи 5)
A = Q1–2 + Q2–3 + Q3–1.
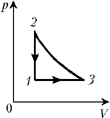
Количество теплоты, полученное газом,
равно
Qi = Q1–2 + Q2–3.
Следовательно, КПД рассматриваемого
цикла равен 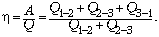
По условию задачи, T2 = T3
= Tmax. Поэтому
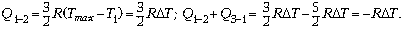
Таким образом, 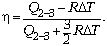
Отсюда 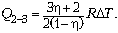 В изотермическом процессе количество
теплоты, полученное от термостата, равно работе
газа Q2–3 = A2–3.
В изотермическом процессе количество
теплоты, полученное от термостата, равно работе
газа Q2–3 = A2–3.
Ответ. 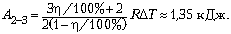
Продолжение в № 3/06