О.Ю.Шведов, С.Д.Варламов, М.В.Семёнов, А.И.Елантьев, В.А.Погожев,
Д.Э.Харабадзе, Д.А.Ягнятинский, А.А.Якута,К.В.Дмитриев, В.В.Птушенко,
А.В.Андрианов, К.В.Башевой, А.Р.Зильберман, Ю.В.Старокуров
yakuta@genphys.phys.msu.ru

Продолжение. См. № 1, 3, 5/05

65-я Московская региональная олимпиада
школьников по физике-2004

7–11-й классы

10-й класс (окончание)

Задача 2

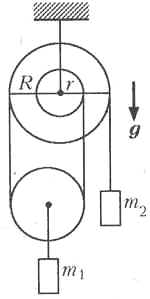
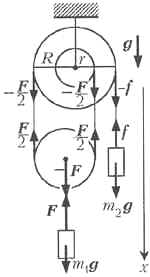
Найдите ускорение груза массой m₁ в системе, изображённой на рисунке. Блоки невесомы, нить невесома, нерастяжима и не проскальзывает по верхнему двухступенчатому блоку радиусами r и R. Один конец нити закреплён на этом блоке, к другому концу прикреплён груз массой m₂. Участки нити, не лежащие на блоках, вертикальны, трение в осях блоков и о воздух отсутствует, ускорение свободного падения равно g.

Решение

Обозначим силу натяжения подвеса, на котором закреплён груз m₁, через F. Тогда сила натяжения нити на вертикальных участках по обе стороны от нижнего блока равна F/2 – из-за невесомости этого блока и нити, а также из-за отсутствия трения в оси блока и трения о воздух. Силу натяжения нити, действующую на подвешенный к ней груз m₂, обозначим через f. Так как двухступенчатый блок невесом и трение в его оси и о воздух отсутствует, то сумма моментов сил натяжения нити, действующих на него, равна нулю:

Отсюда

Поскольку система из таких блоков не даёт выигрыша в работе, то при смещении нижнего груза, например, вниз, верхний груз сместится вверх, и будет справедливо соотношение между перемещениями грузов x₁ и    x₂ : Fx₁ + fx₂ = 0. Отсюда с учётом найденной связи между силами F и f  получаем Таким образом, связь проекций a₁ и a₂ ускорений грузов на вертикальную ось (уравнение кинематической связи) имеет вид:

Запишем уравнения движения грузов в проекциях на ту же ось:

Для решения получившейся системы подставим во второе уравнение выражения для a₂ и f:

Умножим второе уравнение на и сложим результат с первым уравнением. В результате получим

Отсюда

Задача 3

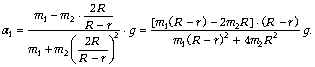
Лёгкая нерастяжимая нить длиной L = 2 м удерживается за концы так, что они находятся на одной высоте рядом друг с другом. На нити висит кусочек проволоки массой M = 1 г, изогнутый в виде перевёрнутой буквы U. Нить выдерживает максимальную силу натяжения F = 5 Н. Концы нити одновременно начинают перемещать в противоположных горизонтальных направлениях с одинаковыми скоростями  = 1 м/с. В какой-то момент нить не выдерживает и рвётся. На какую максимальную высоту относительно уровня концов нити взлетит кусочек проволоки? Ускорение свободного падения g = 10 м/с², сопротивлением воздуха пренебречь.

Решение

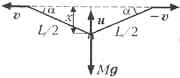
Изобразим нить в тот момент времени, когда она ещё не порвалась, но вот-вот порвётся. Пусть в этот момент расстояние от проволочного грузика до линии, вдоль которой перемещаются концы нити, равно х, а скорость грузика равна u. Так как нить нерастяжима, то проекция скорости грузика и проекция скорости конца нити на направление нити должны быть одинаковы. Следовательно, cos = usin. Поэтому

Из условия задачи видно, что . Поэтому угол, который составляют две половинки нити в момент перед разрывом, близок к 180°, а угол мал. Это означает, что , т.е. Уменьшение расстояния x на малую величину x приведёт к тому, что скорость u увеличится на u. При этом изменения скорости u и величины x связаны друг с другом соотношением

Разделим данное соотношение на величину малого промежутка времени t, за который эти изменения произошли, и учтём,

что

В соответствии со вторым законом Ньютона ускорение u/t равно сумме всех действующих на груз сил, разделённой на его массу. Так как перед самым обрывом нити равнодействующая сил натяжения равна то

Предположим, что не только , но и (потом нужно будет обязательно проверить, выполняется ли на самом деле это неравенство!). В этом случае

и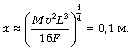

Неравенство действительно выполняется. Теперь можно определить скорость груза в момент разрыва нити:

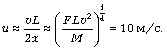
Следовательно, груз после разрыва нити взлетит на высоту

Задача 4

Идеальный одноатомный газ находится в гладком вертикальном цилиндре под невесомым поршнем, на котором стоит груз массой m. Снаружи цилиндра вакуум, теплообмен газа с окружающими телами отсутствует. Над газом совершают процесс, состоящий из n стадий, на каждой из которых массу груза увеличивают в одно и то же число раз по сравнению с предыдущим значением, а затем дожидаются установления равновесия. Конечная масса груза равна М. Во сколько раз изменится объём газа после завершения этого процесса? Решите задачу в общем случае, а затем получите приближённый ответ для n = 2004, Ускорение свободного падения равно g, действием силы тяжести на газ можно пренебречь.

Примечание. При малых и справедливо соотношение

Решение

Пусть масса груза на каждой стадии увеличивается в раз по сравнению с предыдущим значением. Ясно, что Рассмотрим процесс на k-й стадии. Пусть в начале этой стадии поршень площадью S находится в равновесии на высоте h_k–1, температура газа в цилиндре равна T_k–1, вес груза на поршне составляет а давление газа равно В момент, когда на поршень поставили следующий перегрузок, энергия системы стала равна

После затухания колебаний поршень опустится и остановится на высоте h_k, а энергия системы в конце рассматриваемой стадии станет равна

где Так как теплообмен газа с окружающими телами отсутствует, то в соответствии с законом сохранения энергии

Отсюда

Следовательно, после n стадий процесса объём газа изменится в

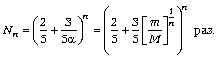
Получим теперь приближённый ответ для При больших n в соответствии с примечанием к условию задачи имеем

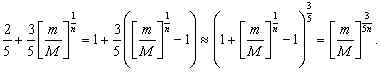
Таким образом, при объём газа изменится в раз, т.е. результат не зависит от n и годится, в частности, для n = 2004. При получаем

т.е. объём газа уменьшится в раза.

Задача 5

Два школьника на уроке физики собрали самодельные приборы для измерения сопротивлений – омметры, – состоящие из последовательно соединённых батарейки, резистора и амперметра, причём эти элементы у каждого школьника были разные. Потом они откалибровали свои приборы, подключая к ним резисторы известного сопротивления, и нанесли на шкалы амперметров эти значения сопротивлений. Далее школьники решили вместе измерить неизвестное сопротивление R_x резистора, одновременно подключив параллельно к нему оба своих прибора с соблюдением одинаковой полярности батареек. При этом один прибор показал значение сопротивления, равное R₁, а второй – R₂. Каково истинное значение R_x?

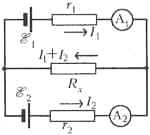
Решение

Нарисуем схему разветвлённой электрической цепи, получившейся у школьников после подключения их приборов к неизвестному резистору. Сопротивления r₁ и r₂ включают в себя сопротивления использовавшихся школьниками резисторов, а также внутренние сопротивления соответствующих батареек и амперметров.

Согласно правилам расчёта разветвлённых цепей постоянного тока, сумма токов в каждом узле разветвлённой цепи равна нулю, а сумма падений напряжений вдоль замкнутых контуров, на которые можно разбить эту цепь, равна суммарной ЭДС в этих контурах. Отсюда, выбрав направления текущих в участках цепи токов, как показано на рисунке, получаем:

Заметим, что при измерении сопротивления резистора R_x одним из самодельных омметров через этот омметр течёт ток (здесь i = 1, 2), так что показание каждого омметра связано с текущим через него током формулой I_iR_х = _i – I_ir_i. Поэтому записанную выше систему уравнений можно переписать в виде:

откуда

Складывая эти равенства, получим

Отсюда

11-й класс

Задача 1

Два однородных концентрических обруча жёстко скреплены невесомым стержнем АВ и могут вращаться без трения в вертикальной плоскости вокруг неподвижной горизонтальной оси О, проходящей через их центр. К обручам прикреплены лёгкие упругие нити, другие концы которых неподвижно закреплены на потолке и стене, как показано на рисунке. Масса и радиус внутреннего обруча равны m и R соответственно, а внешнего – 2m и 2R. В начальном положении системы, когда обе нити не растянуты, длина вертикальной нити равна l₀, длина горизонтальной 2l₀. Коэффициент упругости на растяжение у горизонтальной нити равен k, у вертикальной 2k. Обручи поворачивают из начального положения по часовой стрелке на угол ₀ и отпускают с начальной скоростью, равной нулю. Найдите период колебаний системы, считая, что нити абсолютно гибкие, гладкие и при растяжении наматываются на обручи.

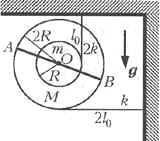
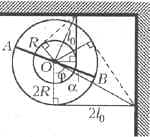
Решение

При повороте обручей по часовой стрелке на угол от начального положения удлинение вертикальной нити при её наматывании на внутренний обруч радиусом R составит а удлинение горизонтальной нити при наматывании на внешний обруч радиусом 2R будет равно Сила натяжения вертикальной нити при этом будет равна а горизонтальной Таким образом, на систему из двух обручей будет действовать суммарный возвращающий момент сил, равный R • 2kR + 2R • 2kR = 6kR² и пропорциональный угловому смещению обручей от положения, в котором обе нити были не растянуты.

По аналогии с гармоническими колебаниями в системе, состоящей из груза массой m, подвешенного на пружине жёсткостью k, для которой модуль возвращающей силы F пропорционален смещению x груза от положения равновесия (F = kx), можно утверждать, что в нашей системе вращательное движение обручей при натянутых нитях будет также происходить по гармоническому закону Круговая частота колебаний для груза на пружине, равная может быть найдена, например, как квадратный корень из отношения коэффициента при x² в выражении для потенциальной энергий W_пот = kx²/2 к коэффициенту при квадрате скорости в выражении для кинетической энергий (точкой над переменной принято обозначать её производную по времени). Пользуясь данной аналогией, можно найти частоту в нашем случае таким же образом. Для этого запишем выражения для потенциальной и кинетической энергии нашей системы с учётом того, что линейная скорость внутреннего обруча а внешнего – :

Отсюда получаем, что а время t₁, за которое система перейдёт из положения с углом отклонения ₀ к положению с = 0, когда нити не растянуты, равно 1/4 периода соответствующих гармонических колебаний:

Далее система будет вращаться по инерции с угловой скоростью которую она приобретёт к моменту t₁, до тех пор, пока нити снова не натянутся. Поскольку запасённая в упругих нитях потенциальная энергия к моменту времени t₁ перейдёт в кинетическую энергию обручей: то

Когда нити вновь (и одновременно!) натянутся, система, вращаясь с постоянной угловой скоростью   повернётся на угол за время

В дальнейшем за время, равное t₁, кинетическая энергия вращательного движения обручей снова превратится в потенциальную энергию растянутых нитей, и потом весь процесс будет повторяться. Таким образом, период колебаний нашей системы будет равен

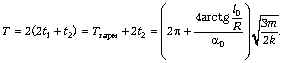
Заметим, что период таких колебаний, как видно из ответа, зависит от величины угла поворота обручей ₀ из начального положения.

Продолжение в № 9