О.Ю.Шведов, C.Д.Варламов, М.В.Семёнов, А.И.Елантьев, В.А.Погожев,
Д.Э.Харабадзе, Д.А.Ягнятинский, А.А.Якута, К.В.Дмитриев, В.В.Птушенко,
А.В.Андрианов, К.В.Башевой, А.Р.Зильберман, Ю.В.Старокуров
yakuta@genphys.phys.msu.ru

Продолжение. См. № 1, 3/05

65-я Московская региональная олимпиада школьников по физике-2004

8-й класс (продолжение)

Задача 3

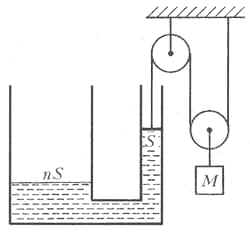
U-образная трубка заполнена водой плотностью (см. рисунок). Узкое колено этой трубки с площадью сечения S закрыто невесомым поршнем, к которому привязана нить, перекинутая через неподвижный и подвижный блоки. Широкое колено трубки, площадь сечения которого в n = 2 раза больше, чем у узкого, открыто. К оси подвижного блока подвешен груз массой M, и система находится в равновесии. На какое расстояние сдвинется груз, если в открытое колено трубки долить воду массой m, а к грузу массой M прикрепить дополнительный груз массой m? Считать, что поршень всё время касается поверхности воды, трения нет, нить и блоки невесомы.

Решение

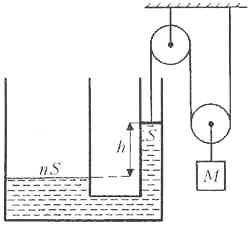
Поскольку подвижный блок даёт выигрыш в силе в два раза, то сила натяжения нити вдвое меньше веса груза. В состоянии равновесия вес груза равен Mg, поэтому разность уровней воды h в коленах трубки определяется из условия и равна, таким образом, После увеличения массы груза на m разность уровней увеличится на Пусть теперь после увеличения массы груза долили воду массой m в открытое колено трубки, и полное (по сравнению с начальным) повышение уровня воды в узком колене составило величину y.

Тогда, поскольку при навешивании дополнительного груза разность уровней воды в коленах трубки увеличилась на в открытом широком колене уровень воды должен повыситься на При этом изменение объёма воды равно Отсюда

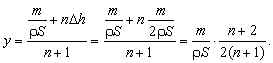
Груз, очевидно, опустится вниз на расстояние

9-й класс

Задача 1

На горизонтальной поверхности стоит круглое пластмассовое блюдце (см. рисунок) с нижним и верхним радиусами R₁ = 6 см и R₂ = 8 см и массой m = 5 г.

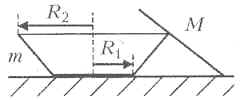
На край блюдца и стол опирается металлический нож массой M, центр тяжести которого расположен на середине его длины. Какую долю от длины ножа может составлять его часть, нависающая над блюдцем, чтобы система оставалась в равновесии? Решите задачу при M = 10 г, M = 20 г и M = 40 г. Трение между ножом и поверхностью стола отсутствует, а коэффициент трения между ножом и блюдцем достаточно большой, так что нож не скользит по блюдцу.

Решение

Рассмотрим сначала условия равновесия ножа. На него действуют (см. рисунок): сила тяжести Mg (направлена вниз); сила реакции N со стороны стола (направлена перпендикулярно столу, вертикально вверх, поскольку трение отсутствует); сила F со стороны блюдца (направлена не обязательно перпендикулярно ножу, т.к. трение между ножом и блюдцем присутствует). Из условия равновесия ножа F + Mg + N = 0 находим, что сила F должна быть вертикальна.

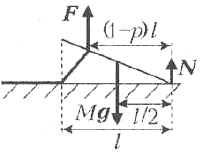
Величины сил F и N можно найти, воспользовавшись правилом моментов, записанным относительно точки опоры ножа на стол. Пусть над блюдцем нависает доля длины ножа, равная p, а длина проекции ножа на стол равна l. Тогда момент силы тяжести положителен и равен Mg • l/2 (сила Mg вращает нож против часовой стрелки), момент силы F отрицателен и равен –F • (1 – p)l (сила F вращает нож по часовой стрелке), и сумма этих моментов сил должна быть равна нулю:

откуда

При этом

Так как нож давит на стол, то   Отсюда следует, что

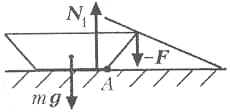
Рассмотрим теперь условия равновесия блюдца. На него действуют (см. рисунок) направленная вниз сила –F со стороны ножа, сила тяжести Mg и сила реакции опоры со стороны стола N₁. Поскольку момент силы тяжести относительно точки A положителен и равен mg • R₁, момент силы –F отрицателен и равен –F(R₂ – R₁), а момент силы N₁ должен быть также отрицательным, то из условия равновесия блюдца получаем

Отсюда:

Следовательно, кроме уже полученного первого условия при равновесии системы должно выполняться и второе условие

При нарушении первого условия будет опрокидываться нож, а при нарушении второго – блюдце. При M = 10 г условия имеют вид: отсюда  При М = 20 г условия имеют вид: ; отсюда: . При M = 40 г второе условие имеет вид но, поскольку p > 0, оно не будет выполняться никогда,  и равновесие системы в этом случае невозможно.

Задача 2

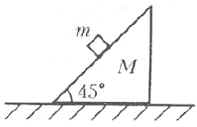
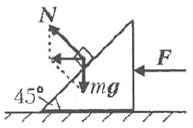
На гладкой горизонтальной плоскости находится клин массой М с углом 45° при основании. По его наклонной грани может двигаться без трения небольшое тело массой m (см. рисунок). Чему должна быть равна и куда (вправо или влево) направлена горизонтальная сила, приложенная к клину, чтобы ускорение тела массой m было направлено: (а) вертикально; (б) горизонтально; (в) составляло угол 45° с вертикалью? Клин не опрокидывается, ускорение свободного падения равно g.

Решение

На тело массой m действуют сила тяжести mg и сила реакции опоры N со стороны клина.

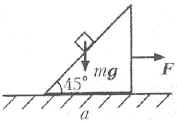
(а) Ускорение тела может быть направлено вертикально, только если сила реакции опоры равна нулю (см. рисунок). При этом величина ускорения тела будет равна g, т.е. оно будет свободно падать. Для того чтобы при падении тела оно не касалось клина с углом при основании 45°, клин должен двигаться вправо с ускорением Следовательно, к клину нужно приложить направленную вправо силу

(б) Как видно из следующего рисунка, ускорение тела будет горизонтально, если

При этом равнодействующая сил, приложенных к телу, равна по модулю mg и направлена влево. Поэтому ускорение тела направлено влево и равно по величине g. Для того чтобы в процессе движения клин давил на тело с необходимой силой N, он также должен двигаться влево с таким же по величине ускорением g. Чтобы сообщить и клину, и телу такое ускорение, к клину необходимо приложить направленную влево силу

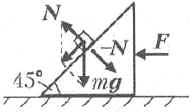
(в) Для того чтобы ускорение тела составляло угол 45° с вертикалью, сила реакции опоры, как видно из рисунка, должна быть по величине равна При этом, очевидно, клин должен покоиться (в противном случае он выскользнет из-под тела). На клин со стороны тела действует сила –N с направленной вправо горизонтальной составляющей, равной по величине mg/2. Чтобы её компенсировать, к клину необходимо приложить такую же по величине силу, направленную влево: F = mg/2.

Задача 3

Внутри куска льда без воздушных пузырей находится вмёрзший камень, плотность которого  = 2000 кг/м³, т.е. вдвое больше, чем у воды ( = 1000 кг/м³). Масса куска льда вместе с камнем М = 3 кг, а температура равна 0 °C. Этот кусок льда опустили в ведро объёмом V = 10 л с водой, причём оказалось, что ведро заполнено по самые края, а над поверхностью воды выступает только 5% от общего объёма куска льда с камнем. Через некоторое время, после того как часть льда растаяла, кусок льда полностью погрузился в воду и продолжал плавать, не касаясь в течение длительного времени ни дна, ни стенок ведра. Найти массу камня и температуру воды в ведре до опускания в него куска льда. Удельная теплоёмкость воды C = 4,2 кДж/(кг • °C), плотность льда  = 900 кг/м³, удельная теплота плавления льда  = 335 кДж/кг. Теплообменом с окружающей средой и тепловым расширением тел пренебречь.

Решение

Согласно условию плавания, вес куска льда с камнем должен равняться весу вытесненной воды. Следовательно, объём вытесненной воды (объём подводной части «айсберга») равен M/ = 3 л, объём воды в ведре равен V – M/ = 7 л, начальная масса воды в ведре m_в = V – M = 7 кг. Обозначим через V_к и V_л объём камня и начальный объем льда. По условию задачи, из воды вначале выступает только 5% от суммарного объёма льда и камня. Поэтому объём их погружённой части равен объёму вытесненной воды: 0,95(V_к + V_л) = M/, а суммарная масса равна Следовательно,

Масса камня и начальная масса льда равны

Обозначим конечную массу льда через Тогда сила тяжести, действующая на «айсберг» по окончании таяния, когда он плавает внутри воды с температурой 0 °C, уравновешивается силой Архимеда. Следовательно,

Отсюда

Следовательно, растаяла масса льда На плавление льда массой потребовалось количество теплоты которое было отнято от воды в ведре при её охлаждении от начальной температуры t до 0 °C: откуда

Задача 4

Прибор для измерения сопротивлений состоит из батарейки с напряжением  резистора сопротивлением R = 10 Ом и амперметра, соединённых так, как показано на рисунке a. На амперметр нанесена шкала, показывающая значение сопротивления резистора, подключаемого к клеммам 1 и 2. С помощью данного прибора пытаются измерить сопротивление электрической цепи, изображённой на рисунке б, которая состоит из источника напряжения и резистора. Оказалось, что показания прибора зависят от полярности подключения к нему этой цепи: в одном направлении показание прибора равно r₁ = 20 Ом, в другом – r₂ = 5 Ом. Найти напряжение источника и сопротивление r резистора. Батарейка, источник напряжения и амперметр имеют пренебрежимо малое внутреннее сопротивление.

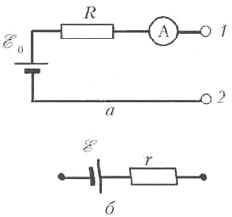
Решение

Показание прибора равно r, если ток через амперметр равен Таким образом, в электрических цепях, изображённых на рис. а и б, токи равны:

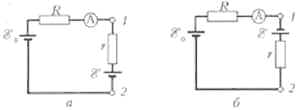
При этом сопротивления цепей на этих рисунках одинаковы и равны R + r, а суммарные напряжения батарейки и источника равны и соответственно. Отсюда

Следовательно,

и

Далее

откуда

10-й класс

Задача 1

Две одинаковые дощечки плывут вдоль берега по прямому широкому каналу, вода в котором течёт с постоянной скоростью, одинаковой по всей ширине канала. В некоторый момент времени дощечкам сообщили скорость относительно воды, равную по величине  = 1 м/с. При этом скорость первой дощечки оказалась перпендикулярной берегу в связанной с ним неподвижной системе отсчёта, а скорость второй дощечки оказалась перпендикулярной берегу в системе отсчёта, связанной с водой. Через достаточно большое время, когда движение дощечек относительно воды прекратилось, расстояние от первой дощечки до берега увеличилось на s₁ = 4 м, а от второй – на s₂ = 5 м. Найти скорость течения воды в канале.

Решение

В системе отсчёта, связанной с водой, дощечки проплывут до полной остановки одинаковое расстояние. Поскольку вторая дощечка движется в этой системе отсчёта перпендикулярно берегу, это расстояние как раз и равно s₂. Следовательно, первая дощечка сместилась тоже на расстояние s₂, и при этом её смещение перпендикулярно берегу составило s₁ (см. рисунок).

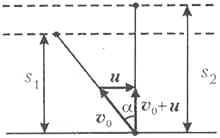
Следовательно, смещение первой дощечки параллельно берегу равно Угол между скоростями дощечек в системе отсчёта, связанной с водой, определяется из соотношения

При переходе в систему отсчёта, связанную с берегом, начальные скорости дощечек складываются со скоростью течения воды в канале u. Следовательно, для первой дощечки

Продолжение в № 7