Задача 3
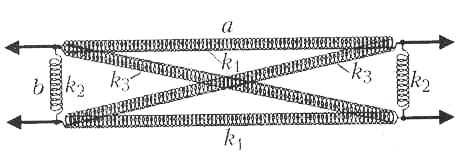
Прямоугольная рама образована тремя
парами пружин с разными коэффициентами
жёсткости (см. рисунок). Все пружины не
деформированы и в углах рамы шарнирно соединены
друг с другом. Известно, что отношение длинной и
короткой сторон рамы a/b = 25, а отношение
коэффициентов жёсткости диагональных и
поперечных пружин k3/k2 = 100.
Раму растягивают, прикладывая к ней четыре
одинаковые силы вдоль длинных сторон, как
показано стрелками на рисунке. При этом длина
рамы a увеличивается на ![]() = 0,001a. Найти
относительные изменения ширины рамы
= 0,001a. Найти
относительные изменения ширины рамы
![]() и
её площади
и
её площади ![]() при таком растяжении.
при таком растяжении.
Решение
При действии на раму в продольном направлении внешних сил Fвн все пружины будут деформироваться: продольные и диагональные – растягиваться, а поперечные – сжиматься. Вследствие этого возникнут силы упругости, действующие на шарниры. Равновесное состояние рамы установится при равенстве нулю суммы сил, действующих на каждый шарнир.
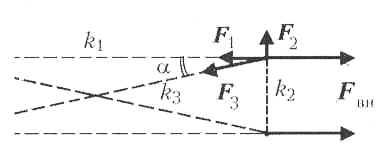
Обозначим угол между диагональю
недеформированной рамы и её длинной стороной
через ![]() , а
силы упругости, действующие на шарнир со стороны
продольной, поперечной и диагональной пружин, –
через F1, F2,
и F3 соответственно (см.
рисунок). Так как относительное удлинение рамы в
продольном направлении
, а
силы упругости, действующие на шарнир со стороны
продольной, поперечной и диагональной пружин, –
через F1, F2,
и F3 соответственно (см.
рисунок). Так как относительное удлинение рамы в
продольном направлении ![]() a/a очень мало, то при
рассматриваемой деформации угол
a/a очень мало, то при
рассматриваемой деформации угол ![]() практически не
изменится. Поэтому условие равновесия шарнира в
поперечном направлении имеет вид
практически не
изменится. Поэтому условие равновесия шарнира в
поперечном направлении имеет вид ![]() Учтём, что
Учтём, что ![]() и
и ![]() Удлинение
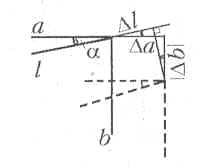
Удлинение ![]() l диагональной пружины определим
при помощи чертежа (см. рисунок):
l диагональной пружины определим
при помощи чертежа (см. рисунок):
![]()
Отсюда получим:
![]()
и
![]()
Так как b = a ![]() , то
, то
![]()
Учитывая, что ![]() b отрицательно (рама в
поперечном направлении сжимается),
b отрицательно (рама в
поперечном направлении сжимается), ![]()
![]() окончательно найдём
окончательно найдём
![]()
т.е. относительное изменение ширины рамы составляет около 10%. Относительное изменение площади рамы при этом равно:
![]()
Так как ![]() то
то ![]()
Мы видим, что в данном случае площадь рамы при её растяжении уменьшается. Это свидетельствует о том, что объём тела при растяжении может не только увеличиваться (как это имеет место для большинства упругих тел), но и уменьшаться. Приведённая в задаче модель показывает, каким может быть внутреннее строение вещества (например, некоторого полимера), обладающего такими необычными свойствами.
Задача 4
Маленький заряженный шарик массой m
шарнирно подвешен на невесомом непроводящем
стержне длиной l. На расстоянии 1,5l слева
от шарнира находится вертикальная заземлённая
металлическая пластина больших размеров.
Стержень отклоняют от вертикали вправо на угол ![]() и
отпускают без начальной скорости. В ходе
начавшихся колебаний стержень достигает
горизонтального положения, после чего движется
обратно, и процесс повторяется. Найдите заряд
шарика. Ускорение свободного падения равно
и
отпускают без начальной скорости. В ходе
начавшихся колебаний стержень достигает
горизонтального положения, после чего движется
обратно, и процесс повторяется. Найдите заряд
шарика. Ускорение свободного падения равно ![]() .
.
Решение
Поскольку в условии сказано, что при колебаниях процесс повторяется, то потерями энергии можно пренебречь. Для решения задачи воспользуемся законом сохранения энергии: в крайних положениях, когда шарик останавливается, сумма его потенциальной энергии в поле силы тяжести и энергии электрического поля, имеющегося в системе, должна быть одна и та же.
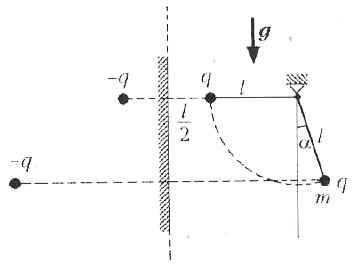
Электрическое поле в пространстве
справа от пластины, как нетрудно показать,
совпадает с полем, которое создавалось бы в
отсутствие пластины двумя зарядами (+q и –q),
расположенными зеркально симметрично по
отношению к поверхности пластины. Действительно,
суммарный потенциал, создаваемый двумя такими
зарядами в каждой точке плоскости симметрии
системы, равен нулю, и, таким образом, в эту
плоскость можно поместить тонкую заземлённую
пластину. Все силовые линии заряда +q при
этом будут замыкаться на её правой поверхности,
индуцированный заряд на которой, очевидно, будет
равен –q. Если теперь удалить заряд
–q, находящийся слева от пластины, и снять
индуцированный заряд +q с левой поверхности
пластины, то справа от неё поле не изменится, а
поле слева исчезнет. Поэтому все точки
пространства слева от тонкой пластины будут
иметь одинаковый потенциал, и это пространство
можно заполнить проводником, что не скажется на
поле справа.
Таким образом, энергия электрического
поля, имеющегося в нашей системе, равна половине
электростатической энергии ![]() взаимодействия двух
точечных зарядов +q и –q, расположенных
на расстоянии r друг от друга. В начальном
положении это расстояние равно
взаимодействия двух
точечных зарядов +q и –q, расположенных
на расстоянии r друг от друга. В начальном
положении это расстояние равно ![]() а в конечном r2
= l. Отсчитывая потенциальную энергию в поле
силы тяжести от начального положения шарика,
запишем закон сохранения энергии:
а в конечном r2
= l. Отсчитывая потенциальную энергию в поле
силы тяжести от начального положения шарика,
запишем закон сохранения энергии:
![]()
Отсюда
![]()
и
![]()
Задача 5
В вертикальный цилиндрический стакан
налита вязкая жидкость коэффициентом
преломления n = 1,5. Сверху в стакан
вертикально падает параллельный пучок света
постоянной интенсивности. Стакан с жидкостью
раскрутили вокруг его оси до угловой скорости ![]() = 1
рад/с, при этом высота столба жидкости на оси
стакана стала равной h = 30 см. На сколько
процентов изменилась после раскручивания
интенсивность света, падающего вблизи центра дна
стакана? Ускорение свободного падения
= 1
рад/с, при этом высота столба жидкости на оси
стакана стала равной h = 30 см. На сколько
процентов изменилась после раскручивания
интенсивность света, падающего вблизи центра дна
стакана? Ускорение свободного падения ![]() = 10 м/с2,
поглощением света в жидкости и отражением его
внутри стакана пренебречь.
= 10 м/с2,
поглощением света в жидкости и отражением его
внутри стакана пренебречь.
Решение
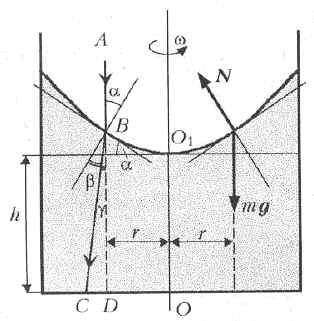
При вращении жидкости вместе со
стаканом её поверхность искривляется,
вследствие чего параллельный пучок света после
преломления становится расходящимся. Рассмотрим
небольшой элемент жидкости, находящийся на её
поверхности на расстоянии r от оси вращения O1O.
На него действуют сила тяжести ![]() и суммарная сила
давления N со стороны остальной
жидкости. Эти силы обеспечивают равномерное
вращение рассматриваемого элемента по
окружности с угловой скоростью
и суммарная сила
давления N со стороны остальной
жидкости. Эти силы обеспечивают равномерное
вращение рассматриваемого элемента по
окружности с угловой скоростью ![]() , сообщая ему
центростремительное ускорение. Уравнения
движения этого элемента в проекциях на
горизонтальную и вертикальную оси имеют вид:
, сообщая ему
центростремительное ускорение. Уравнения
движения этого элемента в проекциях на
горизонтальную и вертикальную оси имеют вид:
![]()
![]()
где ![]() – угол наклона к горизонту поверхности
жидкости в данной точке. Отсюда
– угол наклона к горизонту поверхности
жидкости в данной точке. Отсюда ![]()
Луч света, идущий вдоль оси вращения O1O,
не преломляется. Рассмотрим ход луча ABC,
преломляющегося в точке B на небольшом
расстоянии r от оси вращения. В соответствии
с законом преломления света ![]() Углы
Углы ![]() ,
, ![]() и
и ![]() можно считать малыми, так что
можно считать малыми, так что
![]()
![]()
![]() Отсюда
Отсюда
![]()
![]()
Далее найдём расстояние OC от оси вращения до точки падения преломленного луча на дно стакана:
![]()
Пока жидкость была не раскручена, все
лучи, идущие на расстоянии, меньшем r, от оси O1O,
не преломлялись и попадали в круг радиусом r
на дне, т.е. энергия этого пучка распределялась по
площади S0 = ![]() После раскручивания
жидкости эти же лучи попадут в круг на дне
радиусом OC, т.е. энергия пучка распределится
по площади
После раскручивания
жидкости эти же лучи попадут в круг на дне
радиусом OC, т.е. энергия пучка распределится
по площади
![]()
Поэтому интенсивность света, падающего вблизи центра дна стакана, изменится в
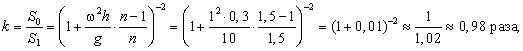
т.е. уменьшится на ![]()
Задача 1
На длинном шоссе на расстоянии 1 км друг от друга установлены светофоры. Красный сигнал каждого светофора горит в течение 30 с, зелёный – в течение следующих 30 с. При этом все автомобили, движущиеся со скоростью 40 км/ч, проехав один из светофоров на зелёный свет, проезжают без остановки, т.е. тоже на зелёный свет, и все следующие светофоры. С какими другими скоростями могут двигаться автомобили, чтобы, проехав один светофор на зелёный свет, далее нигде не останавливаться?
Решение
Нарисуем график движения автомобиля. По горизонтальной оси будем откладывать время t в секундах, по вертикальной – пройденный путь s в километрах. Изобразим на этом графике сигналы каждого из светофоров: запрещающие красные – в виде чёрточек, а разрешающие зелёные – в виде промежутков между ними.
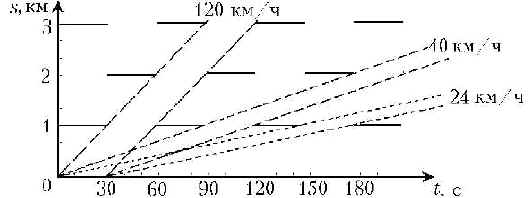
Тогда график движения любого автомобиля, движущегося без остановок, должен проходить только через светлые промежутки. Заметим, что расстояние 1 км между соседними светофорами автомобиль, движущийся со скоростью 40 км/ч, проедет за 1/40 ч = 90 с. Таким образом, он сможет проехать следующий светофор без остановки, только если разрешающие и запрещающие сигналы светофоров будут распределены так, как показано на рисунке. Из графика видно, что автомобиль будет двигаться без остановок на светофорах в том случае, если он будет преодолевать 1 км за 30 с, 90 с, 150 с, … , 30 + 60n с, … , где n = 0, 1, 2, … Следовательно, скорость автомобиля, которая требуется для движения по шоссе без остановок на светофорах, может быть равна
![]() 120 км/ч, 40 км/ч, 24 км/ч…
120 км/ч, 40 км/ч, 24 км/ч…
Задача 2
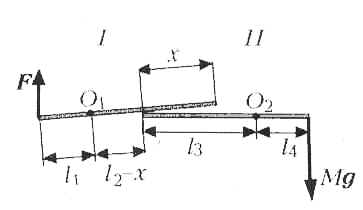
Для того чтобы измерить подъёмную силу воздушного шарика, Вася использовал два тонких невесомых рычага I и II, оси которых O1 и O2 параллельны. Рычаги горизонтальны и имеют область «перекрытия» длиной x. К свободному концу рычага I Вася привязал шарик, а на свободный конец рычага II поставил гирю массой M. Какой должна быть подъёмная сила F шарика, чтобы он мог перетянуть гирю? А какой она должна быть, чтобы гиря перетянула шарик? Расстояния l1, l2, l3 и l4 считать известными.
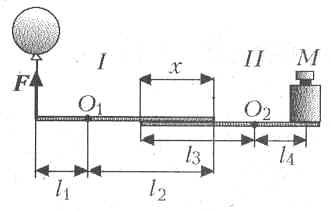
Решение
Рассмотрим по отдельности два возможных случая.
1. Шарик перетягивает гирю. При этом рычаг I касается рычага II в точке, находящейся на расстоянии x от левого конца рычага II, и левое плечо рычага II становится равным l3 – x. В точке касания рычаги действуют друг на друга силами f1 и f2, равными по величине (f1 = f2 = f) и противоположными по направлению. Используя правило рычага, получим условия, которые должны выполняться для того, чтобы шарик мог перетянуть гирю:
![]() – для рычага I;
– для рычага I;
– для рычага II.
Отсюда:
![]()
2. Гиря перетягивает шарик. В этом случае рычаг II касается рычага I в точке, находящейся на расстоянии x от правого конца рычага I, и правое плечо рычага I становится равным l2 – x. При этом неравенства, полученные из правила рычага, выглядят так:
– для рычага I;
– для рычага II.
Отсюда:
![]()