t
= 4 °С. Необходимые данные возьмите из таблицы
по свойствам материала опоры. (Указанный дистанционный курс (16-004) читается уже третий год и неизменно пользуется успехом. Каждый год автор даёт новую подборку задач для контрольных работ. – Ред.)
КОНТРОЛЬНАЯ № 2 (окончание)
Задача 8 (9–10-й кл.). Вертикальная
опора (6 баллов). Вертикальная стальная опора в
виде буквы I в основании здания имеет длину L =
6 м и массу M = 300 кг. Она подвержена нагрузке
сверху F = 300 кН. Вычислите изменение
внутренней энергии балки, если её температура
понизилась на t
= 4 °С. Необходимые данные возьмите из таблицы
по свойствам материала опоры.
Свойства стали
Плотность........................................................................................ 7700–7900 кг/м3
Теплоёмкость.................................................................................... 460 Дж/(кг · К)
Коэффициент термич. расшир. ..................................................... 11 · 10–6 1/град.
Модуль Юнга................................................................................................ 210 ГПа
[Задача из учебника «Физика» (т. 1) Д.Джанколи, но, как известно, там нет решений.]
Решение
Изменение внутренней энергии происходит в результате работы внутренних сил. Перечислим возможные слагаемые:
1) изменение внутренней энергии за счёт работы диссипативных сил (нагревание тела);
2) изменение потенциальной энергии сил деформации за счёт опускания центра масс.
Оценим каждое из слагаемых:
1) W2
= cM · t =
–300 · 4 · 460 
–5,5 ·
105 Дж;
2) W3 =
0. Поясним последнюю оценку. Запишем известные
соотношения законов упругости (Гука и Юнга): 
(здесь L – текущее значение
деформации балки), и выражение для энергии
деформации: 
200
Дж. Эта величина определена, по условию,
значением внешней силы (внешняя нагрузка F) и
остаётся постоянной при тепловом расширении
(сжатии). Иное дело, если бы опора стояла (лежала)
без начальной деформации, а при изменении
температуры упёрлась бы или потянула за собой
места закрепления.
Всё-таки оценим значение статической и температурной деформаций:
1,5 · 10–3
м.
Отметим, что изменение потенциальной энергии сил гравитации за счёт опускания центра масс описывает работу внешней силы и не относится к изменению внутренней энергии. Тем не менее это значение можно оценить:
Таким образом, главный вклад в изменение внутренней энергии – охлаждение балки: внутренняя энергия уменьшилась на 5,5 · 105 Дж.
Задача 9 (11-й класс). ТЭЦ на реке (3 балла). На берегу реки расположена тепловая станция. Произведённый пар подаётся в турбины при температуре 250 °С, а израсходованная вода сливается в реку при температуре 20 °С. При какой температуре забирается вода выше станции по течению реки, если мощность станции 1000 МВт, а расход речной воды 40 м3/с? Для удобства оценки считайте, что тепловая станция работает по обратимому циклу Карно. [По материалам учебника «Физика» Д.Джанколи.]
Решение
Для цикла Карно справедливо
соотношение между совершённой работой A и
полученным от котла теплом Qi через
температуру нагревателя Th (пар) и
холодильника Tc (вода в реке): 
Ясно также, что A = Qi – Qp,
где Qp – отдаваемое тепло, которое в
конечном счёте (в результате цепочки
преобразований
нагревание–пар–конденсация–охлаждение),
нагревает воду на 
Используя эти соотношения, а также
выражение для мощности N = A/t, получаем: 
Значит, вода забирается при температуре 12,5 °С.
Задача 10 (11-й класс). Электромагнит (6
баллов).Обмотка электромагнита имеет полное
сопротивление Z1 = 10 Ом и коэффициент
мощности сos
1=
0,6. Каким станет новое значение коэффициента
мощности сos 2,
если параллельно к обмотке присоединить
конденсатор реактивным сопротивлением Z2
= 7 Ом?
Решение
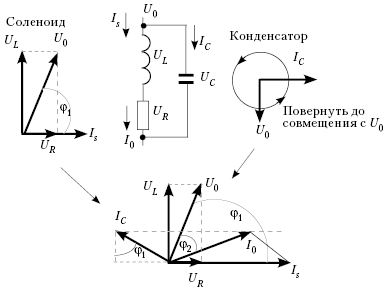
Построения векторных диаграмм
представлены на рисунке. Слева от схемы –
диаграмма ветви электромагнита, cправа –
диаграмма ветви с конденсатором, внизу –
совмещение диаграмм на основании равенства
приложенного напряжения U0 для
получения результирующей диаграммы с полным
током I0. Задача состоит в получении
выражения для сos2,
между током I0 и напряжением U0.
На первом этапе запишем очевидные соотношения: Ic
= U0/Z2 и Is = U0/Z1
(ловушка: I0 = U0/Z12, где
– реактивные
импедансы не подчиняются этому правилу, так
можно делать лишь в комплексной форме, когда
учитываются и фаза, и модуль).
Далее учтём равенство вертикальных
проекций векторов токов Ic и I0:
IC cos1
= I0 sin (1
– 2).
Теперь запишем соотношение для горизонтальных проекций этих векторов:
I0 сos (1 – 2)
= Is – IC sin1.
Осталось решить систему этих двух уравнений.
Исключим ток I0: 
Подставим значения токов и исключим U0:
Преобразуем:
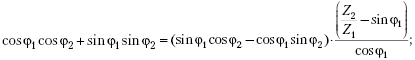
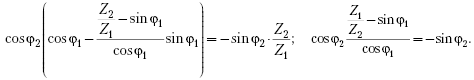
Отсюда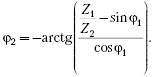 
И окончательно:
