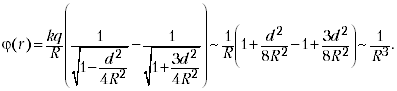
Продолжение. См. № 10/08

А.А.КНЯЗЕВ,
ЛПН, СГУ им. Н.Г.Чернышевского, г. Саратов

Олимпиадный материал в повседневной работе учителя физики

Дистанционный курс: концепция, анализ контрольных работ, выполненных слушателями, и решения задач, предлагавшихся в 2007/08 уч.г.

(Указанный дистанционный курс (16-004) читается уже третий год и неизменно пользуется успехом. Каждый год автор даёт новую подборку задач для контрольных работ. – Ред.)

КОНТРОЛЬНАЯ № 1 (окончание)

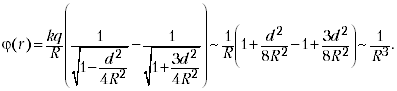
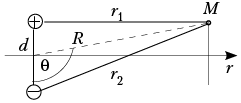
Как видим, здесь авторы опрометчиво воспользовались известным результатом, согласно которому модуль напряжённости поля диполя определяется формулой при фиксированном значении угла . Далее, имея в виду соотношение между напряжённостью поля и потенциалом E = –d/dr, просто мысленно учли понижение степени знаменателя на единицу при интегрировании. Однако в поставленной формулировке условия изменились, и теперь угол на направление точки М не постоянен – он уменьшается с увеличением расстояния до точки.

Впрочем, возможно, в текст закралась опечатка (и такое сейчас не редкость). В любом случае возможность проникновения ошибок, которые впоследствии очень трудно оспорить (на это просто нет времени), является важным доводом против использования тестов дистанционного типа на решающих (выпускных или вступительных) экзаменах. Предлагаемые в настоящее время тесты требуют жёсткого ответа в противоположность устному экзамену, допускающему непродолжительный, но последовательный диалог для каждого шага получения ответа на вопрос. Лишь так можно выявить реальный уровень подготовленности с учётом естественного волнения учащегося на экзамене. Иное дело – использование тестов для оперативной работы в процессе обучения. Тут никто и не возражает: «троечники», «зубрилки» и «законники» получат своё, а с толковыми ребятами можно и побеседовать. А борьбу с коррупцией нужно начинать не с образовательных учреждений.

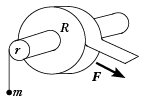
5. Скотч (5 баллов). На вал радиуса r прочно насажен моток нерастяжимой липкой ленты (скотча) радиусом R. На этом же валу на лёгкой нити висит груз массой m. Если ленту тянуть с силой F, то груз будет подниматься с постоянной скоростью. С какой силой F'  надо тянуть ленту, чтобы с той же скоростью поднимать груз 2m? [Всероссийская олимпиада по физике, 1998, г. Чебоксары. 9-й кл.]

Решение. Здесь важно понять действие силы F и удачно выделить её составляющие. Рабочий рисунок показывает, что тангенциальная составляющая силы создаёт момент вращения, а нормальная действует против сил сцепления слоёв ленты-скотча, и эта составляющая остаётся неизменной по модулю при увеличении полной силы. Теперь можно записать две пары соотношений статики:

Отсюда получаем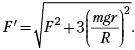

КОНТРОЛЬНАЯ № 2

Тема задания: для предложенного фрагмента олимпиадного пакета из десяти задач сделайте рисунки, подробные расчёты, пояснения, проведите анализ, выскажите мнение о возможности частичного или полного его использования в своей работе, другое мнение.

В задании приведены фрагменты олимпиады среднего уровня (школьная, районная, городская). Выбраны одна-две задачи для каждого класса. По сути, это тренировка перед выполнением третьего, заключительного задания, где нужно будет уже самому составить школьную олимпиаду. Предлагаемые ниже задачи также частично составлены автором.

Задача 1 (8-й класс). Проба воды на льдине (1 балл). Во время экспедиции на дрейфующей льдине пробурили скважину для отбора проб воды. Какую толщину имеет эта льдина, если глубина до поверхности воды в скважине оказалась равной 1,5 м? Считайте, что плотности льда и воды равны соответственно 900 кг/м³ и 1000 кг/м³. [Сборник Кировских олимпиад.]

Решение

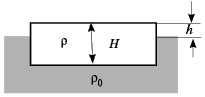
Конечно, здесь возможно и эвристическое решение, к которому чаще всего обращаются школьники младших классов. Действительно, лёд плавает в воде, выступая над поверхностью воды на одну десятую часть своего объёма, значит, толщина льдины 15 м.

А вот формальное решение: условие плавания льдины выражает равенство силы гравитационного притяжения и силы Архимеда: mg = F_A. Запишем это равенство через плотности и объёмы: ₀S(H – h)g = SHg. Отсюда получим для толщины льдины:

Задача 2 (8–9-й классы). Замерзание воды (1 балл). Ожидается, что ночью температура на улице понизится от 0 °С до –5 °С. Сколько (минимум) литров воды нужно вылить под решётки, на бетонный пол ещё не отапливаемого хранилища, чтобы температура в нём осталась нулевой? Какую толщину будет иметь этот слой воды? Размеры хранилища 5 10 3 м³. Удельная теплоёмкость воздуха 1,007 кДж/(кг · К). Удельная теплота отвердевания (плавления) льда 333 кДж/кг. Плотности воздуха и воды равны соответственно 1,4 кг/м³ и 1000 кг/м³. Наличие овощей при оценке можно не учитывать (почему?).

Решение

Тепло, выделившееся при замерзании воды, идёт на нагревание воздуха: CSHT = ₀Sh, откуда   То есть объём воды, который нужно вылить на пол, по оценке, равен 5 10 10^–4 10³ дм³ = 5 л. При замерзании этой воды тепла выделится около 1,7 МДж. Такое же количество теплоты можно получить при сжигании в помещении 150 г дров открытым пламенем.

При таянии это же тепло будет отнято у воздуха хранилища. Однако этот процесс может растянутьcя во времени или прийтись на весну, когда окажется только на пользу. Учёт присутствия овощей для минимальной оценки необязателен, т.к. биологические процессы в овощехранилище идут, как правило, с выделением тепла, а значит, овощи немного подогревают сами себя.

Задача 3 (8–9-й классы). Охлаждение крыши веранды (3 балла). В жаркий солнечный день основное количество теплоты поступает в виде энергии излучения Солнца. Солнечная постоянная J₀ 1 кВт/м². Укроем крышу веранды площадью 20 м² слоем материала, впитывающего влагу. Какое минимальное количество воды нужно испарять за 1 ч, чтобы температура в помещении оставалась постоянной? Удельная теплота испарения воды r = 2,4 МДж/кг.

Решение

Представим, что вода просто налита на крышу. Её нужно испарить в таком количестве, чтобы скомпенсировать приход тепла: J₀ST = r₀Sh, откуда ~ 1мм, т.е. около 20 л/ч.

Примечательно, что для испарения (и применения этой формулы) нет необходимости нагревать воду до температуры кипения: если вода испарилась, то унесено данное количество теплоты. Другое дело, что при кипении отключается другой канал – расход теплоты на нагревание. В этой задаче учёт нагревания воды только усложняет расчёт, но практически не влияет на результат, поскольку здесь сT r, а открытый воздух и явно выраженная конвекция увеличивают скорость процесса испарения.

Не так уж и плох способ. Возможно, что кондиционер и окупит себя при решении проблемы в доме или в душном автомобиле. Но для тента на даче, балконе или веранде лучше придумать простое приспособление для непрерывного полива крыши, ведь каждому известно, насколько прохладнее на берегу речки или в лесу, – процесс тот же.

Задача 4 (9-й класс). «Ядерная» физика (3 балла). В военных записках о войне Пруссии против Дании (1864 г.) отмечается, что в ночном бою «при удачном попадании в бронированный борт броненосца видели сверкание внезапно раскалившегося ядра» (т.е. нагрев больше, чем на 700 °С). Оцените, какую скорость имели перед ударом железные ядра массой 12 кг, если в тепло переходит почти 80% кинетической энергии. Известно, что половина из этой части расходуется на нагрев борта, причём передняя четверть ядра раскаляется примерно втрое сильнее, чем остальная часть. Удельная теплоёмкость железа около 0,46 кДж/(кг · К). [Задача составлена буквально по тексту книги Ф.Энгельса «Диалектика природы». А вот с цифрами пришлось повозиться.]

Решение

Здесь всё просто. Удачный удар – лобовой. Определим количество теплоты, идущее на нагревание передней части ядра:

Отсюда следует, что для возникновения подобного эффекта необходима скорость около 900 м/с.

Задача 5 (9-й класс). Галилей (2 балла). Галилей утверждал (1637 г.), что при свободном падении без начальной скорости расстояния, проходимые телом за равные последовательные промежутки времени, относятся между собой как последовательные нечётные числа:
s₁ : s₂ : s₃ : ... = 1 : 3 : 5... Докажите это утверждение и найдите, как соотносятся расстояния, пройденные за третью и шестую секунды. Расчёт проводите без учёта сопротивления воздуха.

Решение

При равноускоренном падении справедлива формула для пройденного пути: Если время измерять промежутками длительностью , то эта формула примет вид Для отрезка пути, пройденного за n-й промежуток, получим:

Преобразуем:

Таким образом, пройденный за n-й промежуток времени путь пропорционален нечётному числу (2n –1). Это и требовалось доказать. Для расстояний, пройденных за последовательные третью и шестую секунды, запишем ряд значений:

Отсюда

Задача 6 (10-й класс). Деревянная броня (2 балла). Подводная часть броненосца «Пётр Великий» (1872 г.) состояла из наружной стальной плиты толщиной 305 мм, скреплённой болтами с дубовой «подушкой» толщиной 330 мм для обеспечения плавучести и амортизации ударов снарядов. Во сколько раз деревянная подушка ослабляла таким образом силу ударов? Сравнительные справочные данные по свойствам брони и дерева приведены в таблице:

Решение

«Пётр Великий» – сильнейший в мире броненосец в 1872 г. (Черноморский флот, 9665 т, 13,5 узлов, первоначальное название «Крейсер»). Средняя сила удара снаряда (или, с 1865 г., торпеды) массой m, летящего со скоростью , может быть определена по основному закону динамики где – длительность удара. Чем больше это время, тем больше ослабляется удар. Для слоистого материала «деревянной брони» время можно оценить как где c – скорость распространения волны сжатия (звука). Поскольку оба слагаемых сравнимы по значению, то сила удара ослаблялась вдвое, т.е. настолько же, насколько ослабила бы её удвоенная толщина брони. Отметим, что броня в то время только что была изобретена. В соответствии с современными технологиями бронезащиты от разрывных и кумулятивных снарядов деревянную подушку следовало бы укрепить снаружи.

Задача 7 (10-й класс). Снаряд (3 балла). Снаряд, выпущенный со скоростью ₀ под углом к горизонту, разрывается на две равные части на некоторой высоте. Одна половина полетела строго параллельно поверхности земли, а вторая – с той же скоростью, строго вертикально. На какой высоте произошёл такой разрыв? [С.П. Кузнецов. Саратовские олимпиады.]

Решение

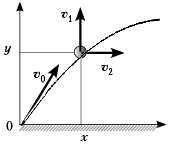
Запишем кинематические соотношения:

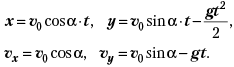
Из условия задачи следует, что в момент разрыва выполняются условия равенства значений горизонтальной и вертикальной проекции импульса (и скоростей, при равных массах). Иначе, в этот момент скорость исходного целого заряда направлена под углом 45° к горизонту.

Отсюда следует: ₀cos = ₀sin – gt.

Получим отсюда значение момента времени и подставим в выражение для вертикальной координаты. Получим:

Далее:

Видно, что неотрицательное решение возможно, если sin > cos, т.е. если начальный угол больше 45°. Итак, при выполнении условий задачи, снаряд разрывается на высоте

Окончание см. в № 17/08