Продолжение. См. № 1, 3, 5, 7/08

К.А.КОХАНОВ < center@extedu.kirov.ru >, М.В.ГЫРДЫМОВ,
П.Я.КАНТОР, Л.И.ВАСИЛЕВСКАЯ,
ЦДООШ, г. Киров

Кировские экспериментальные задачи

Задачи областных и городских олимпиад Кировской области,
2004–2007 гг.

18 (10Г.06). Оцените атмосферное давление.

Оборудование: открытая с обоих концов стеклянная трубка, пластиковая линейка, прозрачный стакан объёмом 0,5 л с холодной водой.

Для организаторов. Трубки следует подбирать высотой не менее 30 см и внутренним диаметром около 10 мм. При таком диаметре на результатах не так сильно сказывается поверхностное натяжение, а водяной столбик не вытекает из трубки при её вытаскивании из воды.

Решаемость: 6/45 = 13%.

Решение. Опускаем трубку длиной L одним концом в воду и измеряем линейкой высоту столба h1 воды в ней. Закрываем находящийся в воздухе конец трубки пальцем и достаём трубку из воды. (Немного воды из трубки вытекает.) Измеряем высоту оставшегося в трубке столба воды h2. Поскольку вода из трубки не вытекает, можно заключить, что атмосферное давление у открытого конца трубки равно давлению столба воды и воздуха p в трубке под пальцем: pа = gh2 + p (1), где – плотность воды.

Давление воздуха р в трубке после вытекания части жидкости можно найти с использованием уравнения Клапейрона–Менделеева:

pаS(L – h1) = pS(L – h2), или          (2)

Подставляя выражение для р в равенство (1), получим

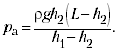             (3)

Эксперимент следует повторить несколько раз, изменяя начальный уровень воды в трубке. После нахождения среднего значения атмосферного давления и средней абсолютной погрешности измерений результат может быть записан так:

pа = pа ср ± pа ср .         (4)

Разбалловка: приведено выражение (1) – 1 балл; записано уравнения Клапейрона–Менделеева и формула (2) – 1 балл; получена конечная формула (3) – 2 балла; выполнены необходимые измерения – 2 балла; получено численное значение атмосферного давления – 1 балл; найдено среднее значение атмосферного давления (по результатам трёх-пяти опытов) – 1 балл; записан численный результат в виде (4) с учётом правила округлений – 2 балла.

19 (10Г.05). Определите относительную влажность воздуха.

Оборудование: два пластиковых стаканчика до 200 мл (один прозрачный), сосуд с ледяной водой (один на всех) и черпаком, сосуд с горячей водой (один на всех) и черпаком, термометр, таблица зависимости давления насыщенных водяных паров от температуры.

Таблица 2. Давление насыщенного водяного пара при разных температурах

t, °C

p, мм рт.ст.

t, °C

p, мм рт.ст.

t, °C

p, мм рт.ст.

t, °C

p, мм рт.ст.

0

4,58

11

9,84

22

19,83

33

37,73

1

4,93

12

10,52

23

21,07

34

39,90

2

5,29

13

11,23

24

22,38

35

42,18

3

5,60

14

11,99

25

23,76

36

44,56

4

6,10

15

12,79

26

25,21

37

47,07

5

6,54

16

13,63

27

26,74

38

49,69

6

7,01

17

14,53

28

28,35

39

52,44

7

7,51

18

15,48

29

30,04

40

55,32

8

8,05

19

16,48

30

31,82

45

71,88

9

8,61

20

17,54

31

33,70

50

92,5

10

9,21

21

18,65

32

35,66

55

118,0

Для организаторов. Для лучшего наблюдения запотевания перед опытами наружные стенки стаканчика следует обезжирить, протерев их сухой тряпкой.

Решаемость: 4/68 = 6%.

Решение. Наливаем в прозрачный стаканчик ледяную воду и опускаем в неё термометр. Через некоторое время наружные стенки стаканчика запотеют. Очень медленно доливаем из второго стаканчика горячую воду, пока не исчезнет роса на стенках. Замечаем температуру, при которой исчезла роса. По таблице определяем парциальное давление водяных паров p в классе, затем, измерив комнатную температуру, определяем максимальное давление водяных паров р0 в классе. По формуле = (p/p0)100% находим относительную влажность воздуха в классе.

Разбалловка: описан способ определения влажности воздуха – 2 балла; получена температура исчезновения росы на стенках стакана – 2 балла; определена относительная влажность воздуха – 2 балла; выполнено несколько измерений и получено среднее значение влажности – 2 балла; найдена погрешность измерений ср – 1 балл; результат записан в виде: = ср ± ср (с учётом правила округлений) – 1 балл.

20 (10О.06). Погрузив иглу шприца в стакан с водой и выдвинув быстрым движением поршень шприца из крайнего нижнего положения в крайнее верхнее, продолжайте удерживать его в этом положении и наблюдайте процесс заполнения шприца водой.

Задание: определите среднюю скорость прохождения воды через штуцер (самое узкое место) полимерного шприца в вышеуказанном процессе.

Оборудование: полимерный медицинский шприц со съёмной иглой, стаканчик с водой, миллиметровая бумага, ножницы, секундомер.

Указания: 1) Не прикладывайте к поршню чрезмерную силу, чтобы он не вышел из корпуса шприца, преодолев сопротивление упора в верхней части; 2) хотя игла шприца предварительно затуплена и никогда не использовалась по прямому назначению, всё-таки соблюдайте осторожность, манипулируя с оборудованием.

Решаемость: 6/22 = 27%.

Решение. Измеряем время t заполнения шприца водой. Скорость воды определяется из соотношения v.jpg (1798 bytes)S = V/t, где S = D2/4 – площадь поперечного сечения штуцера, V – объём шприца. Для определения внутреннего диаметра D штуцера целесообразно использовать вырезанный из миллиметровой бумаги остроко-нечный прямоугольный треугольник. Таким образом, v.jpg (1798 bytes) = 4V/(D2t) (1).

Разбалловка: получена формула для определения скорости воды (1) – 3 балла; описан метод определения внутреннего диаметра штуцера (с помощью треугольника из миллиметровой бумаги) – 2 балла; выполнены необходимые измерения – 1 балл; определена скорость прохождении воды через штуцер шприца – 1 балл; проведены повторные измерения (по крайней мере дважды) и получены значения скорости воды в штуцере – 1 балл; найдена погрешность в определении скорости воды – 1 балл; результат записан в виде: v.jpg (1798 bytes) = v.jpg (1798 bytes)ср ± v.jpg (1798 bytes) – 1 балл.

21 (11Г.05). Определите внутреннее сопротивление батарейки: 1) проведите необходимые измерения и расчёты, считая вольтметр идеальным; 2) сделайте качественную оценку, насколько разумно допущение об идеальности вольтметра.

Оборудование: батарейка, резистор известного сопротивления (1...4 Ом), вольтметр учебный.

Для организаторов. Батарейку лучше взять обычную на 1,5 В, вольтметр – с пределом измерений до 6 В, резистор сопротивлением от 1 до 4 Ом.

Решаемость: 38/86 = 44%.

Решение. У идеального вольтметра бесконечно большое внутреннее сопротивление. Тогда, соединив вольтметр с клеммами батарейки (собрав цепь 1), определяем её ЭДС:

= U1.          (1)

Далее присоединяем к батарейке резистор известного сопротивления и параллельно ему вольтметр (цепь 2). Сила тока I, протекающего по резистору, может быть найдена двояко:

– из закона Ома для замкнутой цепи:

         (2)

– из закона Ома для участка цепи:

             (3)

где r – внутреннее сопротивление батарейки, R – сопротивление резистора, U2 – показания вольтметра в цепи 2.

Решая совместно уравнения (2) и (3), получим

         (4)

Проверим, насколько уместно было считать вольтметр идеальным. Запишем для первого измерения закон Ома для замкнутой цепи: откуда

I1RV = U1 = – I1r.

Далее собираем цепь 3, в которой последовательно соединяем батарейку, вольтметр и резистор. Сила тока в этой цепи откуда I3RV = U3 = – I3(r + R).

Если U1 U3, то I1 I3, значит, RV r и RV R, т.е. предположение об идеальности вольтметра справедливо. В противном случае сделанное допущение ошибочно.

Разбалловка: предложены цепи, позволяющие определить внутреннее сопротивление – 1 балл; записаны уравнения (1)–(3) или им подобные – по 1 баллу за уравнение; получена формула для расчёта внутреннего сопротивления – 2 балла; описана методика проверки допущения идеальности вольтметра – 1 балл; сделаны необходимые измерения для определения r – 2 балла; определено r – 2 балла; получены экспериментальные данные, доказывающие допустимость допущения, – 1 балл.

Продолжение см. в № 11/08