Продолжение. См. № 1/08
4 (8Г.05). Наиболее точно оцените объём пасты в стержне шариковой ручки.
Оборудование: стержень с пастой для шариковой ручки, линейка, миллиметровая бумага, ножницы.
Примечание: не портите и не расходуйте стержень!
Решаемость: 8/72 = 11%.
Решение.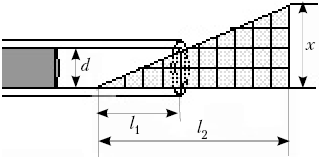 
Объём пасты определяется так: V = Sl,
где l – длина той части стержня ручки, в
которой находится паста, её можно
непосредственно измерить с помощью линейки, S
= 
d2 –
площадь поперечного сечения внутреннего канала
стержня ручки, d – диаметр этого канала.
Итак, искомый объём пасты V = d2l (1). В
эксперименте возникает проблема при измерении
диаметра канала пишущего стержня d,
поскольку точность непосредственного его
измерения линейкой мала. Поэтому можно поступить
так: аккуратно тонкими линиями отчертите на
миллиметровой бумаге узкий прямоугольный
треугольник, а затем вырежьте его. Полученный
треугольник поместите в канал пишущего стержня,
и, опираясь на подобие сторон в указанных на
рисунке треугольниках, определить диаметр
канала стержня. В итоге можно записать
соотношение: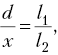 
откуда
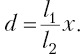(2)
Тогда окончательная расчётная формула примет вид:
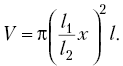(3)
Разбалловка: приведена формула (1) для определения объёма пасты в стержне – 2 балла; описан метод наиболее точного определения диаметра канала стержня и получена расчётная формула (2) – 4 балла; измерена длина той части стержня, которая занята пастой – 1 балл; непосредственно линейкой измерен диаметр канала стержня и на основе этого измерения определён объём пасты – 1 балл; использован метод наиболее точного определения диаметра канала стержня и определены параметры l1, l2 и x – 2 балла; исходя из формулы (2), определён объём пасты – 1 балл.
5 (8Г.06). Оцените объём одной скобы для степлера.
Оборудование: полоска скоб для степлера, кусок миллиметровой бумаги, ножницы или ножик для отламывания скоб (скобы можно отламывать от полоски).
Для организаторов. Каждому ученику следует выдать полоску скоб для степлера
Решение. 
Объём одной скобы V = abc (1), где а – длина скобы, b – ширина скобы, с – толщина скобы. Измерив длину полоски L и сосчитав количество N входящих в неё скоб, можно определить ширину одной скобы: b = L/N (2). Отломив и распрямив одну из скоб, определяем её длину а.
Для нахождения толщины c отделяем от полоски n скоб, выпрямляем у них один конец и укладываем, как показано на рисунке. Измерив толщину полоски l, находим толщину одной скобы: с = l/n (3).
Итак, с учётом формул (1) – (3),
получим: 
Разбалловка: описан метод определения длины одной скобы – 1 балл; определена длина одной скобы – 1 балл; описан метод определения ширины скобы – 1 балл; определена ширина скобы – 2 балла; описан метод определения толщины скобы – 2 балла; определена толщина скобы – 2 балла; выполнено несколько измерений и найдено среднее значение объёма скобы – 1 балл.
6 (8О.04.1). Сравните поверхностные плотности трёх листов бумаги.
Оборудование: три листа бумаги, на одном из которых нанесена миллиметровая сетка, ножницы или лезвия.
Примечание: поверхностной плотностью бумаги называется величина, равная отношению массы бумаги к площади её поверхности.
Решаемость: 4/18 = 22%.
Решение. Из листов нарезаем
одинаковые бумажные полоски и сгибаем их вдоль б
льшей стороны –
получаем бумажные уголки. Из уголков сооружаем
весы: две полоски, вложенные одна в другую,
являются коромыслом, а третья – опорой.
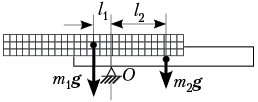
Для сравнения масс и плотностей
взвешиваемые полоски смещаем друг относительно
друга, кладём на полоску-опору и устанавливаем
равновесие. Тогда отношение плотностей полосок
можно найти из условия: m1gl1 = m2gl2,
откуда 
(1),
где 
1 –
поверхностная плотность листа бумаги с
миллиметровыми делениями, 2 – поверхностная плотность
второго листа.
Разбалловка: описан метод определения отношения поверхностных плотностей – 3 балла; получена расчётная формула для определения отношения поверхностных плотностей – 2 балла; проведены однократные измерения – 2 балла; выполнен повторный эксперимент – 1 балл; найдено численное значение искомого отношения поверхностных плотностей – 2 балла.
7 (8О.04.2). Изучите зависимость силы трения скольжения бруска от площади его соприкосновения с горизонтальной поверхностью и от его веса.
Оборудование: прямоугольный брусок, линейка, грузик массой 100 г, динамометр, нить любой длины.
Решаемость: 2/18 = 11%
Решение.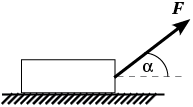 
Для изучения зависимости Fтр(S) брусок по очереди устанавливаем на исследуемую поверхность разными гранями и равномерно тянем за нить динамометром. Динамометр должен располагаться горизонтально, тогда его показания будут соответствовать значению силы трения скольжения. Зависимость имеет вид: Fтр(S) = С, где С – некоторая константа.
При изучении зависимости Fтр(P) последовательно измеряем силу тяги, необходимую для равномерного движения cамого бруска и бруска с грузом при горизонтальном расположении нити. Затем измеряем значения силы тяги при расположении нити под углом к горизонту. При горизонтальном расположении нити значение силы тяги равно величине силы трения. Вес бруска можно определить с помощью динамометра.
При тяге бруска под углом к горизонту
сила трения равна Fcos
. Вес бруска при этом уменьшается на
величину Fsin,
т.е. Р = Fт – Fsin, где Fт –
сила тяжести для одного бруска или бруска с
грузом. Значения cosa и sina определяем из
геометрических соображений, пользуясь линейкой.
По результатам измерений строим график зависимости Fтр(P) = kP, где k – некоторая константа.
Разбалловка: экспериментально показано, что сила трения не зависит от площади контакта бруска с поверхностью – 2 балла; описан метод определения зависимости силы трения скольжения бруска от его веса – 3 балла; снята зависимость силы трения скольжения от веса бруска (по отношению к горизонтальной поверхности) – 3 балла; построен график зависимости – 2 балла.
8 (8О.05.2). Определите коэффициент
поверхностного натяжения жидкости 
.
Оборудование: медицинский шприц вместимостью 5 мл, стаканчик с водой, кусок миллиметровой бумаги, линейка, ножницы.
Примечание: свисающая
капля жидкости удерживается от падения силой
поверхностного натяжения F = l, где l –
длина линии границы с поверхностью твёрдого
тела. Если капля жидкости свисает, например, из
тонкой вертикальной трубочки, то l равна
длине окружности внутреннего отверстия
трубочки.
Решаемость: 6/26 = 25%.
Решение. Используем метод отрыва
капель. В момент отрыва капли модуль силы
поверхностного натяжения F равен модулю
силы тяжести mg, действующей на каплю массой m:
F = mg, или D = mg,
где D – внутренний диаметр сопла шприца.
Отсюда 
Для
определения D вырежем из миллиметровой
бумаги остроконечный прямоугольный треугольник
и вставим его в сопло шприца. Отметим деление
(например, т. А), до которого конус свободно
входит в сопло. Из подобия треугольников ОАВ
и ОСF: 
Массу одной капли найдём, выпуская из шприца жидкость по капельке. Для успеха эксперимента перед опытом из шприца удалим поршень. Воду в шприц набираем так: опускаем шприц в жидкость соплом вниз, ждём, когда баллончик заполнится, закрываем отверстие пальцем. Замечаем по шкале шприца начальный уровень жидкости и, слегка приоткрыв палец, выпускаем часть отдельными каплями со скоростью 1–2 капли в секунду. Масса одной капли m = M/N , где М – масса вытекшей из шприца воды, N – число капель. В итоге
Разбалловка: описан метод определения – 2 балла;
использована возможность повышения точности
эксперимента в определении массы одной капли
(путем выпускания из шприца несколько капель) – 2
балла; получена расчётная формула для – 2 балла; проведены
необходимые измерения – 2 балла; получено
численное значение – 2 балла.
Продолжение см. в № 5/08