13 (9Г.06). Оцените плотность цилиндрического тела.
Оборудование: непрозрачный сосуд с водой, цилиндрическое тело, линейка, динамометр с непроградуированной шкалой.
Указание: сосуд нельзя
считать цилиндрическим; плотность воды 
в = 1000 кг/м3; на
шкале динамометра можно делать отметки.
Для организаторов. Шкала динамометра должна быть заклеена картоном. Если с одним динамометром будут работать несколько школьников, то следует предусмотреть возможность смены шкал. Исследуемое тело должно полностью входить в сосуд с водой.
Решаемость: 11/66 = 17%.
Решение. Взвесим исследуемое тело
в воздухе и в воде, отмечая при этом штрихами
положение указателя динамометра. Затем
проградуируем шкалу динамометра. Пусть действие
тела на пружину в воздухе Р1, а в воде P2.
Тогда сила Архимеда, действующая на тело: FA
= Р1 – Р2. Расстояние между
отмеченными штрихами 
x на шкале динамометра
соответствует действию на пружину найденной
силы Архимеда. Численное значение действующей на
цилиндрическое тело силы Архимеда может быть
рассчитано так: FA= вg(Sh) (1), где S –
площадь основания цилиндрического тела, h –
его высота.
Таким образом, нам известна связь
деформации пружины x с величиной приложенной силы FA.
Учитывая линейную связь между деформацией
пружины с приложенной к ней силой, выполняем по
линейке градуировку динамометра и определяем
численное значение веса тела Р1 в тех
же единицах, что и FA.
Тогда плотность тела 
(2)
Разбалловка: описан метод градуировки динамометра – 2 балла; описан метод определения объёма тела – 1 балл; найден объём тела – 1 балл; рассчитана величина силы Архимеда по формуле (1) – 1 балл; определён вес тела – 3 балла; определена плотность тела по формуле (2) – 2 балла.
14 (9О.04.2). Определите массу железа, которым «начинён» кусок пластилина.
Оборудование: кусок пластилина с железной «начинкой», динамометр, нить, сосуд с водой.
Указания: 1) плотность пластилина считать равной 1,2 г/см3, плотность железа 7,8 г/см3, плотность воды 1,0 г/см3; 2) кусок пластилина НЕ ДЕФОРМИРОВАТЬ!
Решаемость: 18/29 = 62%.
Решение. Динамометром определяем
вес пластилина с «начинкой» в воздухе: Р0
= (mпл + mж)g (1), затем
находим его вес в воде:
P = P0 – FA (2).
Cила Архимеда:
(3)
в, пл, ж – плотности воды,
пластилина и железа соответственно.
Из выражения (1) получаем 
тогда:
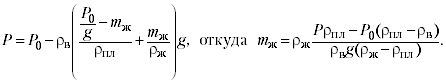(4)
Относительная погрешность измерений может быть найдена так:
(5)
где Р
= Р0 –
половина цены деления динамометра. Погрешность
метода не превышает 10%.
Окончательный результат записывается, например, в таком виде: mж = (95 ± 8) г.
Разбалловка: описан метод
определения массы железной начинки и получены
формулы (1)–(3) – 3 балла; найдена расчётная
формула (4) – 1 балл; произведены необходимые
измерения – 2 балла; получено численное значение
искомой массы – 1 балл; оценена погрешность
измерения массы железной начинки, например, по
формуле (5), – 2 балла, записан окончательный
результат в виде mж = mж ср ± mж ср
– 1 балл.
15 (9О.06). Сравните у двух ламп для карманного фонаря сопротивления и напряжения, на которые они рассчитаны.
Оборудование: две лампы для карманного фонаря с различными сопротивлениями, источник тока (батарейка), соединительные провода, патроны для ламп (или провода, припаянные к лампам).
Решаемость: 11/24 = 46%.
Решение. Количественное
сравнение сопротивлений и напряжений с
использованием предложенного оборудования
невозможно. Качественное сравнение основано на
оценке яркостей лампочек, т.е. выделяемого в них
тепла при прохождении электрического тока.
Соединим лампочки последовательно и подключим к
батарейке. Так как сила тока, протекающего по
лампочкам, одинакова, то, согласно закону
Джоуля–Ленца Q = I2Rt, больше
тепла будет выделяться в лампочке с бoльшим
сопротивлением (соответственно и светиться
будет ярче лампочка с б
льшим сопротивлением). Для сравнения
номинальных напряжений лампочки можно
подключить параллельно к источнику тока. Та
лампочка, которая рассчитана на большее
напряжение, должна светиться с меньшим накалом.
Из формулы Q = I2Rt следует, что
на большее напряжение рассчитана лампочка, у
которой мы обнаружили большее сопротивление.
Обратим внимание, что с помощью параллельного
соединения неодинаковость свечения фиксируется
слабо (особенно если ЭДС батарейки не очень
велика). Поэтому вывод о том, какая лампа
рассчитана на большее напряжение, лучше делать
из анализа последовательного соединения:
лампочка, рассчитанная на большее напряжение, в
этом случае будет светиться ярче.
Разбалловка: указано, что
количественное сравнение рабочих сопротивлений
и напряжений на лампочках при данном
оборудовании невозможно, – 2 балла; выполнен
сравнительный анализ яркостей свечения лампочек
при их последовательном и параллельном
соединениях – 4 балла; экспериментально
выявлено, какая лампочка имеет большее рабочее
сопротивление – 2 балла; экспериментально
выявлено, какая лампочка рассчитана на бльшее напряжение,
– 2 балла.
16 (9О.07.2). Определите плотность неизвестной жидкости.
Оборудование: сосуды с водой и неизвестной жидкостью, две линейки, два одинаковых стакана.
Решаемость: 17/26 = 65%.
Решение. Наливаем в один из
стаканов некоторое количество воды,
уравновешиваем на линейке его и пустой стакан.
Опора находится под центром масс линейки. Тогда mстgl1
= (mст + mв)gl2, где l1
и l2 – плечи сил тяжести пустого
стакана и стакана с водой. Наливаем в пустой
стакан исследуемую жидкость, причём её объём
берём равным объёму воды, так что mв = вV, mж
= жV.
Снова уравновешиваем стаканы с жидкостями на
линейке: (mст + mж)gl3
= (mст + mв)gl4, где l3
и l4 – плечи сил тяжести стакана с
жидкостью и стакана с водой. Исключив из двух
уравнений mст, получим:
Целесообразно повторить измерения не
менее трёх раз, меняя расположение стаканов на
линейке или объём жидкостей (оставляя их
одинаковыми), вычислить ж ср, ж ср
и записать результат в виде:
ж = ж ср ± ж ср.
Разбалловка: приведена идея
метода – 2 балла; получена итоговая формула – 2
балла; выполнены необходимые измерения – 2 балла;
сделан расчёт плотности – 1 балл; произведены
повторные измерения и определена средняя
плотность – 2 балла; записан результат в виде
ж = ж ср ± ж ср – 1 балл.
17 (10Г.04). Определите
коэффициент трения деревянной линейки о
поверхность ровного стола. 
Оборудование: две одинаковые деревянные линейки, скреплённые скотчем с одного края, лист белой бумаги.
Указание: снимать скотч с линеек и наклонять стол запрещается!
Для организаторов. Заранее склейте две сложенные вместе линейки, используя по маленькому кусочку скотча для склеивания наружных и внутренних сторон.
Решаемость: 1/81 
1%.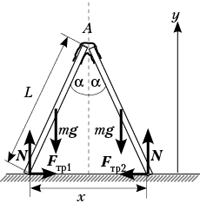 
Решение. Поставьте линейки на поверхность стола. Медленно отодвигайте, допустим, нижний конец левой линейки влево. Как только нижний конец правой линейки начнёт скользить, остановите его. Рядом с линейками положите лист белой бумаги, на котором отметьте положения нижних концов линеек, а затем расстояние х между отметками измерьте одной из линеек. Для симметричной системы двух линеек уравнение 2-го закона Ньютона в проекции на направление оси Y имеет вид: 0 = 2N – 2mg (1) (силы, действующие в т. А, не указаны), значит, N = mg (2).
Для одной из линеек относительно т. А
можно записать равенство моментов сил: 
(3), здесь Fтр
= µN. (4)
Из равенств (2)–(4) получаем 
Причём 
(5)
Опыт следует повторить несколько (N) раз,
определить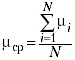 
и
найти среднюю случайную погрешность где µi
– измерение, полученное в i-м опыте, N –
общее количество опытов.
Разбалловка: приведена идея
метода – 2 балла; записана формула (1) – 1 балл;
записана формула (3) – 1 балл; получена
формула (5) – 1 балл; опыт проведён один раз,
измерены величины L и x – 1 балл;
вычислено µ – 1 балл; выполнена попытка повешения
точности измерений: опыт повторен 2–3 раза
(определена повторно величина x) – 1 балл;
найдена случайная погрешность – 1 балл;
правильно записан результат в виде µ = µср ±
µср – 1
балл.
Продолжение см. в № 9/08