Продолжение. См. № 21/06
С.С.ЧЕСНОКОВ, С.Ю.НИКИТИН,
И.П.НИКОЛАЕВ, Н.Б.ПОДЫМОВА,
М.С.ПОЛЯКОВА, проф. В.И.ШМАЛЬГАУЗЕН,
физфак МГУ, г. Москва
sergeychesnokov@mail.ru
Хочу учиться на ВМК!
Задачи, предлагавшиеся на
вступительных экзаменах
на факультет вычислительной математики и
кибернетики МГУ имени М.В.Ломоносова в 2006 г.
I. МЕХАНИКА (окончание)
6
Простейший прибор для измерения объёма
протёкшей через него воды (водомер) представляет
собой 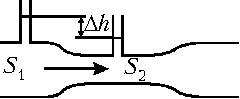 отрезок горизонтальной трубы переменного
сечения, в широкую и узкую части которой
вмонтированы тонкие вертикальные трубки.
Площади сечения широкой и узкой части трубы
равны соответственно S1 = 30 см2 и S2
= 10 см2. Какой объём воды V протекает
через водомер за 1 с, если разность уровней воды в
вертикальных трубках составляет
отрезок горизонтальной трубы переменного
сечения, в широкую и узкую части которой
вмонтированы тонкие вертикальные трубки.
Площади сечения широкой и узкой части трубы
равны соответственно S1 = 30 см2 и S2
= 10 см2. Какой объём воды V протекает
через водомер за 1 с, если разность уровней воды в
вертикальных трубках составляет 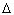 h = 4 см? Течение воды
считать стационарным, капиллярными эффектами в
вертикальных трубках пренебречь. Ускорение
свободного падения принять равным g = 10 м/с2.
h = 4 см? Течение воды
считать стационарным, капиллярными эффектами в
вертикальных трубках пренебречь. Ускорение
свободного падения принять равным g = 10 м/с2.
Решение
Записывая для воды, текущей по трубе
переменного сечения, уравнение Бернулли, имеем:
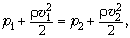
где p1, p2 –
давления воды в широком и узком сечениях трубы, 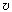 1,
1, 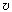 2 – скорости воды в
этих сечениях,
2 – скорости воды в
этих сечениях, 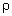 –
плотность воды. Отсюда следует, что
–
плотность воды. Отсюда следует, что
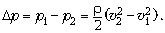
С другой стороны, 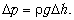 Объём воды, протекающей через
водомер за единицу времени, определяется как
Объём воды, протекающей через
водомер за единицу времени, определяется как
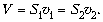
Объединяя записанные выражения,
находим ответ:
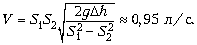
7 Математический
маятник отклонили от положения равновесия на
малый угол 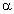 0
= 0,1 рад и отпустили без начальной скорости, после
чего маятник стал совершать гармонические
колебания. Найдите максимальную величину
0
= 0,1 рад и отпустили без начальной скорости, после
чего маятник стал совершать гармонические
колебания. Найдите максимальную величину 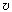 y max
вертикальной составляющей скорости маятника.
Длина маятника l = 0,4 м. Ускорение свободного
падения принять равным g = 10 м/с2.
Считать, что sin
y max
вертикальной составляющей скорости маятника.
Длина маятника l = 0,4 м. Ускорение свободного
падения принять равным g = 10 м/с2.
Считать, что sin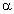
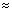
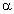 .
.
Решение
Угол отклонения маятника от вертикали
изменяется во времени по закону:
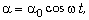
где 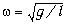 –
циклическая частота. Следовательно, модуль
линейной скорости маятника
–
циклическая частота. Следовательно, модуль
линейной скорости маятника 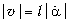 зависит от времени следующим
образом:
зависит от времени следующим
образом:

Величина вертикальной составляющей
скорости маятника равна
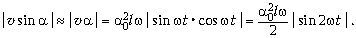
Максимальное значение этой величины
достигается при 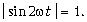
Ответ. 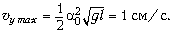
8 По
гладкому жёлобу, имеющему форму дуги окружности,
из точки A без начальной скорости начинает
скользить маленький брусок. Когда этот брусок
проходит половину пути до нижней точки жёлоба
(точки B), из точки A начинает скользить
без начальной скорости второй такой же брусок.
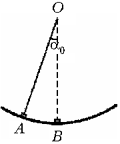
Найдите, какой угол 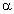 будет составлять с вертикалью
прямая, соединяющая второй брусок с центром дуги
(точкой O), в момент, когда первый брусок
достигнет точки B, если
будет составлять с вертикалью
прямая, соединяющая второй брусок с центром дуги
(точкой O), в момент, когда первый брусок
достигнет точки B, если 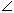 AOB известен и равен
AOB известен и равен 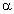 0 (
0 (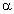 0
0 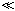 1).
1).
Решение
При движении первого бруска угол 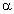 1, задающий его
положение, меняется во времени по закону
1, задающий его
положение, меняется во времени по закону
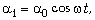
где 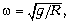 R
– радиус жёлоба. В момент t1, когда
начинает движение второй брусок,
R
– радиус жёлоба. В момент t1, когда
начинает движение второй брусок,
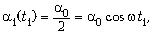
откуда 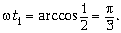 Следовательно, закон движения второго
бруска имеет вид:
Следовательно, закон движения второго
бруска имеет вид:
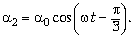
Когда первый брусок в момент времени t2
достигает точки B, 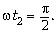 Поскольку искомый угол
Поскольку искомый угол 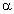 =
= 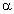 2(t2),
ответ имеет вид:
2(t2),
ответ имеет вид:
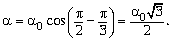
9 На ракете,
взлетающей вертикально с постоянным ускорением а = 1,25g,
установлены маятниковые часы. Точно такие же
часы расположены на поверхности Земли. На какое
время 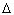 t
будут отличаться показания этих часов по
истечении t = 1 мин после взлёта ракеты? Время t
измерено по часам, находящимся на Земле.
Зависимостью ускорения свободного падения g
от высоты пренебречь.
t
будут отличаться показания этих часов по
истечении t = 1 мин после взлёта ракеты? Время t
измерено по часам, находящимся на Земле.
Зависимостью ускорения свободного падения g
от высоты пренебречь.
Решение
По закону сложения ускорений модуль
ускорения свободного падения в системе отсчёта,
связанной с ракетой, равен g' = g + a.
Следовательно, частота малых колебаний маятника,
установленного на ракете,
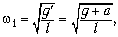
где l – длина нити. Частота
колебаний маятника, находящегося на Земле,
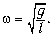
Так как показания часов
пропорциональны числу колебаний маятника за
рассматриваемое время, то по истечении времени
полёта t часы на ракете покажут время
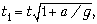
т.е. уйдут вперёд на 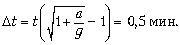
10 Два
шарика массами m и 2m прикреплены к
пружинам жёсткостями k и 8k
соответственно и надеты на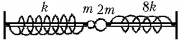 гладкий
горизонтальный стержень. Свободные концы пружин
заделаны в неподвижные стенки так, что в
положении равновесия пружины не деформированы, а
шарики касаются друг друга. Шарик массой m
отводят влево на небольшое расстояние и
отпускают без начальной скорости. Найдите время
гладкий
горизонтальный стержень. Свободные концы пружин
заделаны в неподвижные стенки так, что в
положении равновесия пружины не деформированы, а
шарики касаются друг друга. Шарик массой m
отводят влево на небольшое расстояние и
отпускают без начальной скорости. Найдите время 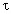 между первым и
вторым соударениями шариков, считая их абсолютно
упругими.
между первым и
вторым соударениями шариков, считая их абсолютно
упругими.
Решение
Пусть скорость шарика массой m
перед ударом равна 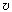 0.
Из законов сохранения импульса и энергии при
упругом столкновении шариков вытекают
равенства:
0.
Из законов сохранения импульса и энергии при
упругом столкновении шариков вытекают
равенства:
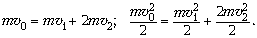
Отсюда 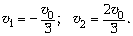 Направив координатную ось OX вправо
и совместив начало координат с положением
равновесия, для координат шариков имеем:
Направив координатную ось OX вправо
и совместив начало координат с положением
равновесия, для координат шариков имеем:
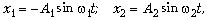
где A1 и A2 –
амплитуды колебаний шариков, 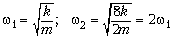 – частоты колебаний.
– частоты колебаний.
Скорости колеблющихся шариков
определяются по формулам:
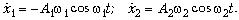
Полагая в этих формулах t = 0 и
используя найденные ранее начальные значения
скоростей 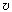 1 и
1 и 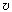 2, получаем, что
2, получаем, что 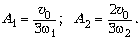 Отсюда следует,
что А1 = А2 = А. Второе
столкновение шариков произойдёт в момент
Отсюда следует,
что А1 = А2 = А. Второе
столкновение шариков произойдёт в момент 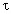 , когда x1 = x2.
Имеем:
, когда x1 = x2.
Имеем:
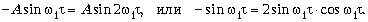
Отсюда
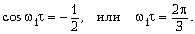
Ответ. 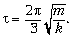
Продолжение в № 7

 отрезок горизонтальной трубы переменного
сечения, в широкую и узкую части которой
вмонтированы тонкие вертикальные трубки.
Площади сечения широкой и узкой части трубы
равны соответственно S1 = 30 см2 и S2
= 10 см2. Какой объём воды V протекает
через водомер за 1 с, если разность уровней воды в
вертикальных трубках составляет
отрезок горизонтальной трубы переменного
сечения, в широкую и узкую части которой
вмонтированы тонкие вертикальные трубки.
Площади сечения широкой и узкой части трубы
равны соответственно S1 = 30 см2 и S2
= 10 см2. Какой объём воды V протекает
через водомер за 1 с, если разность уровней воды в
вертикальных трубках составляет 