Продолжение. См. № 3/07
1 На
металлическую пластинку напыляют серебряное
покрытие, используя пучок атомов серебра,
направленный перпендикулярно пластинке. С какой
скоростью ![]() 0
растёт толщина покрытия, если атомы серебра
оказывают на пластинку давление p = 0,1 Па?
Кинетическая энергия одного атома E = 10–17
Дж, молярная масса серебра M = 108 г/моль, его
плотность
0
растёт толщина покрытия, если атомы серебра
оказывают на пластинку давление p = 0,1 Па?
Кинетическая энергия одного атома E = 10–17
Дж, молярная масса серебра M = 108 г/моль, его
плотность ![]() = 10,5
г/см. Постоянная Авогадро NA = 6,02·1023
моль–1.
= 10,5
г/см. Постоянная Авогадро NA = 6,02·1023
моль–1.
Решение
На площадке пластинки площадью S
за время ![]() осаждается масса серебра
осаждается масса серебра
![]()
где m – масса атома серебра, N0
– число атомов, попадающих на единичную площадку
в единицу времени, ![]() 0
– скорость роста толщины покрытия. Отсюда
0
– скорость роста толщины покрытия. Отсюда
![]()
С другой стороны, давление, оказываемое атомами, осаждающимися на пластинке, равно
p = muN0,
где u – скорость атомов. Следовательно,
![]()
Поскольку ![]() и m = M/NA, ответ имеет вид:
и m = M/NA, ответ имеет вид:
![]()
2 В баллоне
находится смесь азота, кислорода и углекислого
газа, причём массы всех трёх газов одинаковы.
Какова плотность смеси ![]() , если давление смеси p = 105 Па,
а температура t = 27 °C? Молярные массы газов:
азота M1 = 28 г/моль, кислорода M2
= 32 г/моль, углекислого газа M3 =
44 г/моль. Универсальная газовая постоянная R
= 8,3 Дж/(моль · К).
, если давление смеси p = 105 Па,
а температура t = 27 °C? Молярные массы газов:
азота M1 = 28 г/моль, кислорода M2
= 32 г/моль, углекислого газа M3 =
44 г/моль. Универсальная газовая постоянная R
= 8,3 Дж/(моль · К).
Решение
Записывая уравнения состояния компонент смеси, находим их парциальные давления:
![]()
где m – масса каждого из газов, V – объём баллона. По закону Дальтона,
p = p1 + p2 + p3.
Плотность смеси ![]() Объединяя записанные выражения,
получаем ответ:
Объединяя записанные выражения,
получаем ответ:
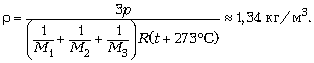
3 В тепловом двигателе, рабочим телом которого является идеальный одноатомный газ, совершается циклический процесс, изображённый на рисунке.
На участке 1–2 давление газа
изменяется пропорционально его объёму. Участок 2–3
– адиабатическое расширение, участок 3–1 –
изобарное сжатие. Чему равен коэффициент
полезного действия двигателя ![]() , если в процессе 1–2
давление газа увеличивается в n = 2 раза, а в
процессе 3–1 объём газа уменьшается в m =
3 раза?
, если в процессе 1–2
давление газа увеличивается в n = 2 раза, а в
процессе 3–1 объём газа уменьшается в m =
3 раза?
Решение
В циклическом процессе работа газа равна алгебраической сумме количеств теплоты, которыми газ обменивается с окружающей средой:
A = Q1–2 + Q3–1.
Газ получает теплоту на участке 1–2. Следовательно, КПД цикла:
![]()
Согласно первому закону термодинамики:
![]()
где ![]() –
количество газа, R – универсальная газовая
постоянная. Учитывая, что
–
количество газа, R – универсальная газовая
постоянная. Учитывая, что
![]()
и используя уравнение состояния газа, выражаем полученное газом количество теплоты в виде:
![]()
Кроме того, по условию, ![]() Следовательно,
Следовательно, ![]()
Ответ: ![]()
4 В
теплоизолированном вертикальном цилиндре под
тяжёлым теплоизолирующим поршнем находится
идеальный одноатомный газ. Расстояние между
поршнем и дном сосуда H. Сверху на поршень
медленно насыпали порцию песка, масса которой m
значительно меньше массы поршня. На какую
величину ![]() U
изменится в результате этого внутренняя энергия
газа? Ускорение свободного падения g.
U
изменится в результате этого внутренняя энергия
газа? Ускорение свободного падения g.
Решение
Изменение внутренней энергии одноатомного идеального газа равно
![]()
где ![]() –
количество газа, R – универсальная газовая
постоянная. Уравнения Клапейрона–Менделеева
для начального и конечного состояний газа имеют
вид:
–
количество газа, R – универсальная газовая
постоянная. Уравнения Клапейрона–Менделеева
для начального и конечного состояний газа имеют
вид:
![]()
Здесь p, V и T – начальные
давление, объём и температура газа; ![]() p,
p, ![]() V и
V и ![]() T – их приращения. Пренебрегая
произведением малых величин
T – их приращения. Пренебрегая
произведением малых величин ![]() p
p![]() V, из этих уравнений находим:
V, из этих уравнений находим:
![]()
Поскольку газ теплоизолирован, из
первого закона термодинамики следует, что p![]() V =
V = ![]() U. Условия
равновесия поршня массой M в начальном и
конечном состояниях имеют вид:
U. Условия
равновесия поршня массой M в начальном и
конечном состояниях имеют вид:
![]()
где S – площадь поршня, p0
– атмосферное давление. Отсюда ![]()
Объединяя записанные выражения,
получаем ответ: ![]()
5 Цилиндрический сосуд площадью сечения S = 10 см2 соединён трубкой с вертикально расположенным капилляром радиусом r = 0,5 мм. В сосуд налили воду и поместили на её поверхность поршень массой M = 100 г.
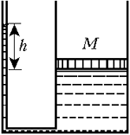
Какова разность уровней воды h в
сосуде и капилляре, если вода смачивает стенки
капилляра? Плотность воды ![]() = 1 г/см3, поверхностное
натяжение воды
= 1 г/см3, поверхностное
натяжение воды ![]() = 73 мН/м, ускорение свободного падения g = 10 м/с2.
= 73 мН/м, ускорение свободного падения g = 10 м/с2.
Решение
Поскольку стенки капилляра смачиваются водой, поверхность воды в капилляре образует вогнутый мениск, имеющий форму полусферы радиусом r, равным радиусу капилляра. Давление воды в капилляре непосредственно под мениском:
![]()
а на уровне поршня
![]()
Здесь p0 – атмосферное давление. Давление воды в сосуде под поршнем:
![]()
Из условия равновесия воды следует, что p1 = p2.
Объединяя записанные равенства, получаем ответ:
![]()