АБИТУРИЕНТУ

С.С.Чесноков, С.Ю.Никитин,
И.П.Николаев, Н.Б.Подымова,
М.С.Полякова, проф. В.И.Шмальгаузен,
физфак МГУ, г. Москва

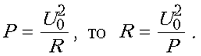
Окончание. См. № 14, 18, 22/02

Хочу учиться на ВМК!

Задачи, предлагавшиеся на вступительных экзаменах на факультет вычислительной математики и кибернетики МГУ им. М.В.Ломоносова в 2001 г.

III. электродинамика

• Напряжение на зажимах генератора постоянного тока U₀ = 220 В, а на зажимах нагрузки U₁ = 210 В. Определите мощность Pл, выделяющуюся в линии между генератором и потребителем, если номинальная мощность нагрузки при напряжении на ней, равном U₀, составляет P = 10 кВт.

Решение

Обозначим через R сопротивление нагрузки. Поскольку номинальная мощность нагрузки при напряжении на ней U₀ равна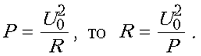

Далее находим ток через нагрузку и передающую линию :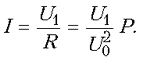

Поскольку падение напряжения в линии равно DU = U₀ – U₁, мощность, выделяющаяся в ней, есть P_л=(U₀–U₁) I. Подставляя сюда найденное значение тока, получаем ответ:

• Катушка индуктивностью L=0,4 Гн и сопротивлением обмотки R=2 Ом подключена параллельно с резистором сопротивлением R₁=8 Ом к источнику с ЭДС и внутренним сопротивлением r = 0,2 Ом. Какое количество тепла Q выделится на резисторе R₁ после отключения источника?

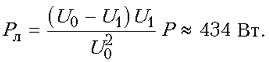
 Решение

При замкнутом ключе через источник течет ток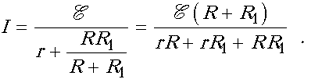

Этот ток разветвляется на два тока I_L и I_R, протекающих соответственно через катушку и резистор R₁ и удовлетворяющих системе уравнений:

I_L + I_R = I;

I_LR = I_RR₁.

Отсюда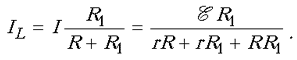

После отключения источника (размыкания ключа) возникающая в катушке ЭДС самоиндукции будет какое-то время поддерживать в цепи, образованной катушкой и резистором R₁, ток

При этом полная мощность выделяющаяся в этой цепи, распределится между катушкой и резистором пропорционально их сопротивлениям:

Следовательно, мощность, выделяющаяся на резисторе, составляет от полной мощности, выделяющейся в этой цепи, следующую долю: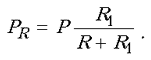

Поскольку данное отношение мощностей не зависит от времени, очевидно, что такую же долю составит и энергия, выделившаяся на резисторе за время существования ЭДС самоиндукции, от полной энергии, выделившейся в цепи. В свою очередь, полная выделившаяся энергия равна энергии магнитного поля в катушке в момент отключения источника. Таким образом, количество тепла, выделившегося на резисторе R1 после отключения источника, равно :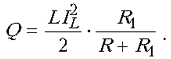

Подставляя в это равенство найденный ранее ток через катушку, получаем ответ:

•  Катушка индуктивностью L = 2 мГн с обмоткой сопротивлением R = 10 Ом и конденсатор емкостью C = 10^–5 Ф подключены параллельно к источнику с ЭДС и внутренним сопротивлением r = 10 Ом. Какое количество тепла Q выделится в контуре после отключения источника?

Решение

При замкнутом достаточно долгое время ключе в цепи устанавливается ток через источник и катушку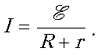

Напряжение на конденсаторе равно напряжению на катушке: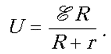

Суммарная энергия заряженного конденсатора и катушки с током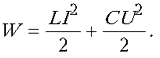

После отключения источника в контуре, состоящем из катушки и конденсатора, возникнут затухающие электромагнитные колебания, в результате которых вся начальная энергия перейдет в тепло:

 IV. Оптика

На равнобедренную стеклянную призму падает широкий параллельный пучок света, перпендикулярный грани BC, ширина которой d = 5 см. На каком расстоянии L от грани BC преломленный приз-мой свет разделится на два не перекрывающихся пучка? Показатель преломления стекла n = 1,5, угол при основании призмы a = 5,7°. При расчетах учесть, что для малых углов tga » sina » a.

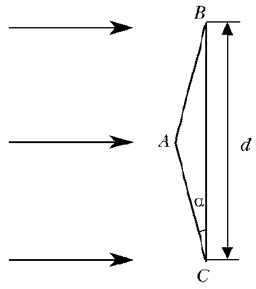
Решение

Каждый из лучей света, падающих на призму, преломляется дважды: на передней и задней ее гранях (см. рисунок).

Закон преломления на этих гранях, записанный с учетом малости углов падения и преломления, дает следующие соотношения:

.

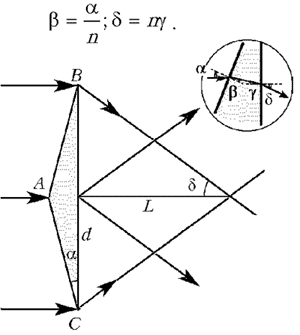
Поскольку g = a – b, получаем для угла преломления значение d = a(n – 1). Из рисунка видно, что пучки света, преломленные призмой, перестанут перекрываться на расстоянии L, удовлетворяющем условию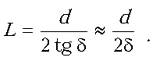

Объединяя записанные выражения, получаем ответ: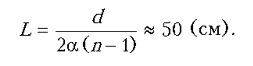

• Точечный источник света находится на главной оптической оси рассеивающей линзы. Если поместить источник в точку А, то его изображение расположится в точке В. Если поместить источник в точку В, то его изображение расположится в точке С. Зная расстояния между точками А и В (l₁ = 20 см) и между точками В и С (l₂ = 10 см), найдите фокусное расстояние линзы f.

Решение

Расположение линзы, источника и его изображения в обоих случаях показано на рисунке.

 Запишем формулу тонкой линзы с использованием для соответствующих расстояний обозначений, приведенных на рисунке: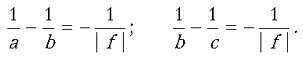

В этих выражениях учтено, что расстояние от линзы до мнимого изображения, а также модуль фокусного расстояния рассеивающей линзы должны войти в формулу линзы со знаком «минус». Кроме того, справедливы также следующие соотношения:

a-b=l₁;  b-c=l₂

Объединяя записанные выражения, получаем ответ: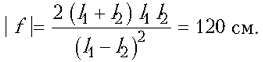

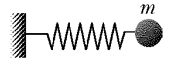I. механика (окончание)

Тело массой m = 1 кг, насаженное на гладкий горизонтальный стержень, совершает гармонические колебания под действием пружины. Какова полная механическая энергия колебаний E, если амплитуда колебаний A = 0,2 м, а максимальное ускорение тела в процессе колебаний a_max = 3 м/с²?

Решение

В проекции на ось, вдоль которой движется тело, уравнение его колебаний под действием пружины жесткостью k имеет вид:

ma = –kx,

где a – ускорение тела, x – его смещение от положения равновесия. Отсюда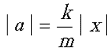

и, следовательно,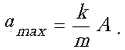

Учитывая, что полная механическая энергия колебаний равна 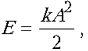, после элементарных преобразований получаем ответ:

• Гиря массой m = 1 кг, подвешенная на пружине, совершает вертикальные гармонические колебания амплитудой A = 0,2 м и периодом Т = 2 с. Определите силу натяжения пружины F в момент, когда гиря достигает нижней точки. Ускорение свободного падения g = 9,8 м/с².

Решение

Будем отсчитывать координату гири относительно точки подвеса пружины, координатную ось OY направим вниз. Пусть длина недеформированной пружины равна l₀, а ее жесткость равна k. Тогда координата положения равновесия гири x0 определится из условия:

mg = k(x₀ – l₀),

откуда 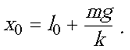 . Гиря совершает колебания относительно положения равновесия с амплитудой A, поэтому в нижней точке координата гири будет x_max= x₀ + A.

По закону Гука, сила растяжения пружины при этом равна F = k(x_max– l₀) = mg + kA.

Жесткость пружины легко найти, зная период колебаний гири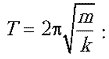

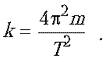
Подставляя найденное k в выражение для силы растяжения пружины, получаем ответ:

.