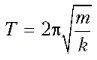 соотношением
соотношением 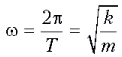 . Обозначив через t0
время, за которое тело проходит от крайнего
положения путь x0/2, можно записать:
. Обозначив через t0
время, за которое тело проходит от крайнего
положения путь x0/2, можно записать: 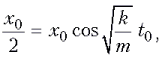 откуда
откуда 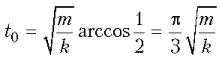 .
.I. Механика
Решение
Выберем в качестве начала отсчета времени момент, когда тело, смещенное от положения равновесия на расстояние x0, отпускают без начальной скорости. Тогда его координата будет меняться со временем в соответствии с выражением
x(t) = x0 cos wt,
где w – круговая частота
колебаний, связанная с периодом колебаний 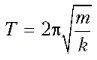 соотношением
соотношением 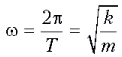 . Обозначив через t0
время, за которое тело проходит от крайнего
положения путь x0/2, можно записать:
. Обозначив через t0
время, за которое тело проходит от крайнего
положения путь x0/2, можно записать: 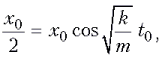 откуда
откуда 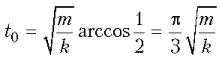 .
.
Средняя скорость тела за время t0 определяется
выражением: 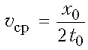
Отсюда 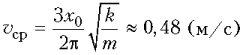
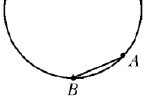 Два
маленьких тела начинают одновременно
соскальзывать без начальной скорости из точки А:
первое – по внутренней поверхности гладкой
сферы до ее нижней точки В, второе – по гладкой
наклонной плоскости АВ. Пренебрегая трением,
найдите, во сколько раз k отличаются времена
движения этих тел от начальной до конечной точек.
Расстояние АВ намного меньше радиуса сферы.
Два
маленьких тела начинают одновременно
соскальзывать без начальной скорости из точки А:
первое – по внутренней поверхности гладкой
сферы до ее нижней точки В, второе – по гладкой
наклонной плоскости АВ. Пренебрегая трением,
найдите, во сколько раз k отличаются времена
движения этих тел от начальной до конечной точек.
Расстояние АВ намного меньше радиуса сферы.Решение
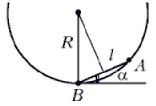 Поскольку
расстояние между точками A и B намного меньше
радиуса сферы, можно считать, что тело,
скользящее по гладкой сферической поверхности
радиусом R, движется как математический маятник
длиной R, совершающий малые колебания. Поэтому
время его движения из точки A в точку B равно
четверти периода
Поскольку
расстояние между точками A и B намного меньше
радиуса сферы, можно считать, что тело,
скользящее по гладкой сферической поверхности
радиусом R, движется как математический маятник
длиной R, совершающий малые колебания. Поэтому
время его движения из точки A в точку B равно
четверти периода 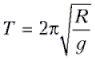 колебаний маятника, т.е.
колебаний маятника, т.е. 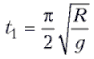 .
.
Тело на гладкой наклонной плоскости, составляющей угол a с горизонталью, движется с ускорением a=2Rsina. Длина наклонной плоскости совпадает с расстоянием между точками A и B, которое, как видно из рисунка, есть l=2Rsina. Следовательно, время движения этого тела из точки A в точку B:
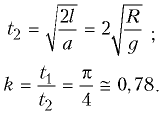
II. Молекулярная физика и термодинамика
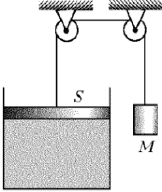 В
цилиндре под невесомым поршнем площадью S = 100 см2
находится 1 моль идеального газа при температуре
t1 = 100 °C. К поршню через два блока на
невесомой нерастяжимой нити подвешен груз
массой М = 17 кг. На какую высоту Dh
поднимется груз, если медленно охладить газ до
температуры t2=0°C? Атмосферное давление p0=10–5
Па, универсальная газовая постоянная R= 8,3 Дж/(моль
· К), ускорение свободного падения принять g=10 м/с2.
Трением пренебречь.
В
цилиндре под невесомым поршнем площадью S = 100 см2
находится 1 моль идеального газа при температуре
t1 = 100 °C. К поршню через два блока на
невесомой нерастяжимой нити подвешен груз
массой М = 17 кг. На какую высоту Dh
поднимется груз, если медленно охладить газ до
температуры t2=0°C? Атмосферное давление p0=10–5
Па, универсальная газовая постоянная R= 8,3 Дж/(моль
· К), ускорение свободного падения принять g=10 м/с2.
Трением пренебречь.Решение
Поршень находится под действием трех сил: силы натяжения нити T и силы давления газа в сосуде pS, направленных вверх, а также силы атмосферного давления p0S, направленной вниз. Поскольку процесс охлаждения газа является медленным, можно считать, что ускорение системы равно нулю и сила натяжения нити в каждый момент времени равна весу неподвижного груза, т.е. T=Mg. Следовательно, поршень находится в равновесии при выполнении условия:
![]()
Как видно из этой формулы, давление газа p при изменении его объема постоянно. Записывая уравнение Клапейрона–Менделеева для начального и конечного состояний газа, получаем
pV1 = RT1; pV2 = RT2,
где T1=(t1 + 273) К; T2= (t2 + 273) К; V1 и V2 – начальный и конечный объемы газа, причем V1 – V2 = DhS. Объединяя записанные соотношения, получаем ответ:
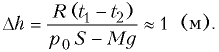
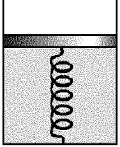 В
вертикально расположенном цилиндре находится
кислород массой m=64 г, отделенный от атмосферы
поршнем, который соединен с дном цилиндра
пружиной жесткостью k=8,3 · 102 Н/м. При
температуре T1=300 К поршень располагается на
расстоянии h=1 м от дна цилиндра. До какой
температуры T2 надо нагреть кислород, чтобы
поршень расположился на высоте H=1,5 м от дна
цилиндра? Универсальная газовая постоянная
R=8,3 Дж/(моль · К), молярная масса кислорода M=32
г/моль.
В
вертикально расположенном цилиндре находится
кислород массой m=64 г, отделенный от атмосферы
поршнем, который соединен с дном цилиндра
пружиной жесткостью k=8,3 · 102 Н/м. При
температуре T1=300 К поршень располагается на
расстоянии h=1 м от дна цилиндра. До какой
температуры T2 надо нагреть кислород, чтобы
поршень расположился на высоте H=1,5 м от дна
цилиндра? Универсальная газовая постоянная
R=8,3 Дж/(моль · К), молярная масса кислорода M=32
г/моль.Решение
Поскольку в условии задачи не сказано, что поршень невесом, будем полагать, что он обладает некоторой неизвестной массой, которую обозначим через M0. Ничего не говорится также про атмосферное давление, поэтому будем считать, что оно действует, и обозначим его через p0. Таким образом, на поршень действуют в общем случае четыре силы: сила тяжести M0g, сила упругости пружины kx (x – удлинение пружины) и сила атмосферного давления p0S, направленные вниз, и сила давления газа в цилиндре pS, направленная вверх. Условия равновесия поршня в начальном и конечном состояниях имеют вид:
![]()
Здесь p1 и p2 – давления газа в начальном и конечном состояниях. Вычитая из второго уравнения первое, получаем:
![]()
С другой стороны, из уравнения Клапейрона–Менделеева, записанного для начального и конечного состояний газа, следует:
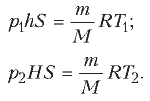
Отсюда вытекает, что 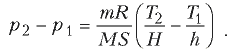
Приравнивая разности давлений газа, найденные
этими двумя способами, после несложных
преобразований получаем ответ: ![]()
Видно, что наличие атмосферного давления и масса поршня не влияют на ответ.
Решение
Обозначим через p1 и p2 давления газов, находящихся в верхней и нижней частях трубки соответственно. Поскольку количества газов в верхней и нижней частях трубки, по условию задачи, различны, а при одной и той же начальной температуре объемы этих частей одинаковы, равновесие поршня возможно только при условии, что он имеет некоторую конечную массу. Обозначив массу поршня через M0, а его площадь через S, запишем условие равновесия поршня в виде:
![]()
Используя уравнение Клапейрона–Менделеева для описания состояния гелия и неона при произвольной температуре T, получаем для разности их давлений следующее выражение:
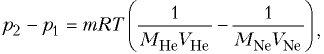
где m – масса каждого из газов, R – универсальная газовая постоянная.
Обозначим через V объем всей трубки. Тогда начальные объемы газов (при температуре T'):
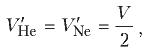
а их конечные объемы (при температуре T''):
![]()
Объединяя записанные равенства, приходим к соотношению:
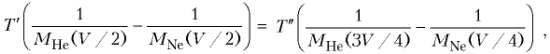
из которого после несложных преобразований
получаем ответ: 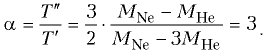
Окончание см. в № 27-28/02