Абитуриенту

С.С. Чесноков, С.Ю. Никитин,
И.П. Николаев, Н.Б. Подымова,
М.С. Полякова, проф. В.И. Шмальгаузен,
физфак МГУ, г. Москва

Хочу учиться на ВМК!

Продолжение. См. № 2, 6, 10/01

Задачи, предлагавшиеся на вступительных экзаменах
на факультет вычислительной математики и кибернетики МГУ им. М.В. Ломоносова в 2001 г.

I. Механика

• Канат длиной l = 2 м переброшен через блок. В начальный момент канат покоится, и по обе стороны блока свешиваются равные его отрезки. Затем в результате незначительного толчка равновесие каната нарушается, и он приходит в движение. Какова будет скорость каната v в тот момент, когда с одной стороны блока будет свешиваться отрезок каната длиной l₁ = 1,5 м? Массой блока и его размерами пренебречь, энергию толчка и трение в блоке не учитывать, ускорение свободного падения g = 10 м/с².

Решение

Когда один из концов каната начнет перевешивать другой, канат придет в движение, причем его ускорение будет все время увеличиваться. В самом деле, поскольку по мере движения будет возрастать масса одной из свешивающихся частей каната и уменьшаться масса другой, будет соответственно увеличиваться сила, сообщающая канату ускорение. Поэтому попытка применить для решения задачи законы динамики обречена на неудачу, т.к. без привлечения высшей математики мы не сможем по переменному ускорению найти скорость тела. Но использование закона сохранения механической энергии позволит легко получить ответ.

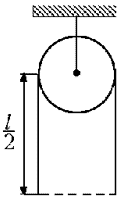
Примем за уровень отсчета потенциальной энергии каната центр блока, обозначим через m массу каната. В начальном состоянии (канат изображен на рисунке штриховой линией) по обе стороны от блока свешиваются одинаковые части каната, длиной l/2 каждая (по условию задачи, длиной отрезка каната, лежащего на блоке, можно пренебречь). Центры тяжести каждой из половин каната (обозначены на рисунке жирными точками) находятся на расстоянии l/4 от уровня отсчета потенциальной энергии, масса каждой из половин равна m/2. Следовательно, начальная потенциальная энергия каната равна

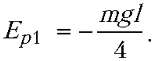
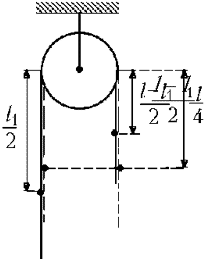
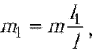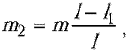В конечном состоянии (канат изображен на рисунке сплошными линиями) слева от блока свешивается отрезок каната длиной l₁ и массой центр тяжести которого находится на расстоянии от уровня отсчета потенциальной энергии; справа от блока свешивается отрезок каната длиной (l – l₁) и массой центр тяжести которого находится на расстоянии (l – l₁)/2 от уровня отсчета потенциальной энергии. В соответствии с этим конечная потенциальная энергия каната равна:

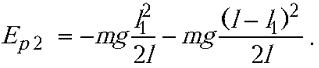
По закону сохранения механической энергии:

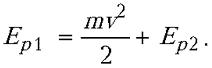
Объединяя записанные выражения, после несложных преобразований получаем ответ:

• На шероховатом столе лежит доска массой М = 1 кг и длиной L = 0,5 м так, что за край стола выступает ее часть длиной aL, где a = 1/4. Какую минимальную скорость v₀ нужно сообщить маленькому бруску массой m=1кг, находящемуся на левом конце доски, чтобы в результате его перемещения левый конец доски приподнялся бы над столом? Коэффициент трения между бруском и доской m=0,1. Доска при движении бруска не скользит по столу. Толщиной доски пренебречь, ускорение свободного падения g=10 м/c².

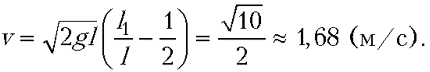
Решение

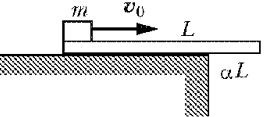
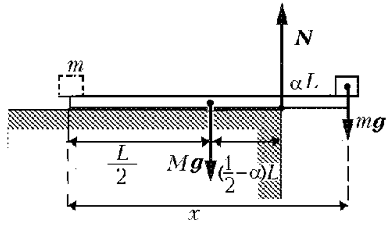
Доска, лежащая на столе, взаимодействует с ним во всех точках соприкосновения. Элементарные силы упругости, действующие со стороны стола на каждый элемент нижней поверхности доски, имеют равнодействующую, величина которой равна суммарному весу доски и кубика, а точка приложения определяется из уравнения моментов. Эту равнодействующую часто называют силой реакции стола. При движении кубика по доске точка приложения силы реакции стола перемещается вправо до тех пор, пока не достигнет его края. В этот момент левый конец доски перестает давить на стол. Дальнейшее перемещение кубика приведет к тому, что доска опрокинется через край стола.

Силы, действующие на доску в момент, когда ее левый конец перестает давить на стол, изображены на рисунке. Из уравнения моментов, записанного относительно оси, проходящей по краю стола, получаем

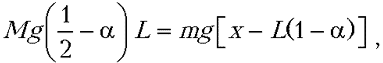
где x – смещение кубика от начального положения. Для того чтобы связать смещение x с начальной скоростью кубика v₀, воспользуемся законом изменения кинетической энергии тела, согласно которому .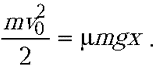

Отсюда 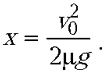. Объединяя это выражение с предыдущим, находим ответ:

• На внутренней поверхности гладкой сферы лежит невесомый стержень с маленькими шариками массами m₁ и m₂ на концах. Длина стержня L равна радиусу сферы. Пренебрегая трением, найдите угол a между стержнем и горизонталью.

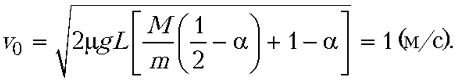
Решение

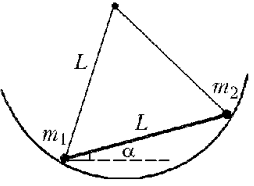
Шарики, насаженные на стержень, находятся в равновесии под действием сил, изображенных на рисунке, где N₁, N₂ – силы реакции сферической поверхности, F₁, F₂ – силы реакции стержня, причем F₁ = –F₂, т.к. стержень невесом и также находится в покое.

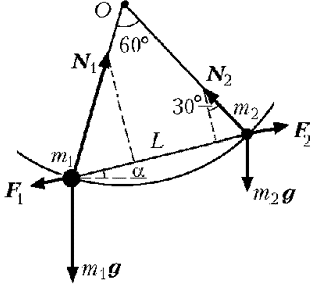
В проекции на направление стержня условие равновесия шариков имеет вид:

Записывая правило моментов относительно осей, проходящих через точки m₁ и m₂, получаем

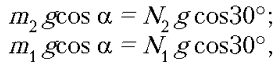
откуда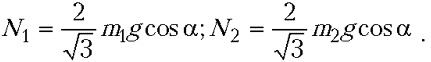 

Подставляя найденные N₁, N₂ в первое соотношение, после несложных преобразований получаем ответ:

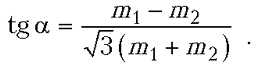
Более простое решение

По условию:

(пусть для определенности m₁>m₂).

По определению центра масс (точка Ц): m₁x = m₂(L – x).

Задача эквивалентна задаче о равновесном положении невесомого треугольника OMK, закрепленного в точке O, тогда OЦ – линия отвеса, а при m₁=m₂ угол a=0.

Г.А. Вомпе

Продолжение в № 18/02

.