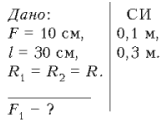
Задача 64. В круглое отверстие в непрозрачном экране вставлена рассеивающая линза фокусным расстоянием F = 10 см, на которую падает пучок световых лучей, параллельных главной оптической оси. На расстоянии l = 30 см от линзы параллельно плоскости линзы расположен экран. Какое фокусное расстояние должна иметь собирающая линза, чтобы при замене ею рассеивающей линзы радиус светлого круга на экране не изменился?
Решение
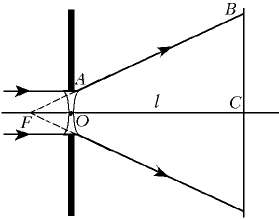
Лучи, проходящие параллельно главной оптической оси рассеивающей линзы, после линзы идут так, что их продолжения пересекаются в фокусе линзы. Границы светлого пятна будут определять лучи, проходящие через края линзы. Построим ход этих лучей и рассмотрим образовавшиеся треугольники AOF и BCF.
Из подобия этих треугольников следует:
где a – радиус линзы, равный радиусу отверстия.
Лучи, параллельные главной оптической оси собирающей линзы, пересекаются в фокусе. Построим ход таких лучей, проходящих по краям собирающей линзы и рассмотрим треугольники A1OF1 и B1C1F1.
Из подобия этих треугольников следует:
Поскольку левые части выражений (1) и (2) одинаковы, то
Отсюда:
Проверка решения по размерности
С этой точки зрения задача решена верно; тогда
Задача 65. Однородный шарик массой m = 60 г лежит на дне пустого стакана. В стакан наливают жидкость так, что объем погруженной в жидкость части шарика в k = 6 раз меньше его общего объема. Плотность материала жидкости в n = 3 раза больше плотности материала шарика. Найдите силу давления шарика на дно стакана. Ускорение свободного падения g = 10 м/с2.
Шарик взаимодействует с Землей, жидкостью и со стаканом, поэтому на него действуют три силы: сила тяжести mg, приложенная к центру шарика, т.к. он однородный, сила Архимеда FА и сила реакции опоры Q. Под действием этих сил шарик находится в равновесии.
Шарик действует на дно стакана силой давления F, которая, по 3-му закону Ньютона, равна по величине силе реакции опоры Q.
Решение
Выберем систему отсчета, связанную с Землей, и будем считать ее инерциальной. Запишем условие равновесия шарика:
mg + FА + Q = 0, или для проекций на ось Oy:
mg – FА – Q = 0.
Используя 3-й закон Ньютона, найдем:
mg – FА – F = 0 Ю F = mg – FА. (1)
По закону Архимеда, FА = rжVп
g, где Vп – объем погруженной в жидкость
части шарика, равный объему вытесненной им
жидкости. Из определения плотности однородного
тела следует, что m = rV, отсюда объем шарика
равен V = m/r. По условию задачи, ![]() тогда:
тогда: ![]()
и выражение (1) принимает вид: ![]()
Проверка решения по
размерности 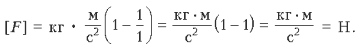
С этой точки зрения задача
решена верно, тогда: ![]()
Задача 66. На круглом плоском зеркале лежит шар радиусом R от глобуса, касаясь центра зеркала Северным полюсом. Каков должен быть минимальный радиус зеркала r, чтобы в нем можно было видеть отражение любой точки Северного полушария и части Южного полушария до широты j = 30°?
Лучи исходят от точки А, лежащей на j градусах южной широты по всем направлениям и формируют изображение А' точки А. Оно мнимое, т.к. в точке А' пересекаются не сами лучи, а их продолжения, и лежит на таком же расстоянии от плоскости зеркала, что и точка А. Другая часть лучей падает на зеркало под разными углами. Для того чтобы изображение существовало, достаточно отражения от зеркала двух лучей, исходящих от точки А. В геометрической оптике толщина лучей равна нулю, поэтому два луча могут проходить по касательной к шару в точке А. Угол падения этих лучей будет минимальным, и если обрезать плоское зеркало по периметру, образованному точками падения таких лучей, исходящих от точек, лежащих на параллели данной широты, то получим зеркало минимального радиуса, когда можно еще увидеть эти точки.
Решение
Из рисунка видно, что:
r = NO + OB;
NO = O1A cos j;
OB = AO • tg j,
т.к. углы ASO1 и j равны как углы с взаимно перпендикулярными сторонами, а углы BAO и ASO1 равны как соответственные. Тогда: r = O1A cos j + AO tg j.
Но AO = R + Rsin j, поэтому
Продолжение читаайте в № 42/01