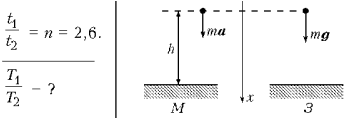
Задача 57. На Марсе время падения тела t1, отпущенного без начальной скорости, с некоторой высоты на поверхность планеты в n = 2,6 раза больше времени падения t2 с той же высоты на Землю. Во сколько раз период малых колебаний математического маятника на Марсе отличается от периода колебаний на Земле? Сопротивление атмосферы не учитывать.
Дано:
Решение
Выберем инерциальную систему отсчета, связанную с неподвижными звездами. Будем считать, что тело падает с небольшой, по сравнению с радиусом Марса, высоты. Вследствие этого движение тела происходит в однородных гравитационных полях Марса и Земли в течение малого промежутка времени. Движения тела являются равноускоренными, а их законы выглядят следующим образом:
где r – радиус-вектор, соединяющий начало координат и положения тела, g – ускорение свободного падения на Земле, a – ускорение свободного падения на Марсе.
Для проекций на ось Ox:
В моменты падения тела на поверхности Земли и Марса имеем:
Отсюда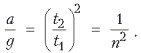 
Период
малых колебаний математического маятника длиной
l определяется формулой 
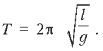Тогда в условиях
Земли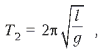 
а в условиях Марса 
.
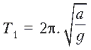Следовательно:
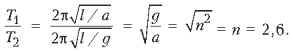
Задача 58. Желоб состоит из двух досок, образующих двугранный угол, у которого ребро горизонтально, а плоскости составляют равные углы a = 30° c горизонтом. В желобе лежит цилиндр массой m = 4 кг, образующая которого параллельна ребру желоба. Какую силу надо приложить в горизонтальном направлении к основанию цилиндра, чтобы он двигался вдоль желоба равномерно? Коэффициент трения между поверхностями желоба и цилиндра m = 0,1.
Анализ условия
Цилиндр взаимодействует с Землей и гранями двугранного угла, поэтому на него действуют три силы: сила тяжести mg и силы реакций Q1 и Q2 со стороны граней желоба. Когда на цилиндр не действует внешняя горизонтальная сила, реакции опор направлены перпендикулярно плоскостям желоба и ребру двугранного угла. При приложении силы F линии действий сил реакции опор наклоняются к ребру желоба: чем больше сила, тем больше наклон, пока цилиндр не сдвинется. Это объясняется тем, что составляющие реакций опор на направление движения цилиндра – силы трения – увеличиваются и достигают своей максимальной величины, называемой максимальной силой трения покоя, после чего они остаются постоянными.
Решение
Выберем систему отсчета, связанную с Землей, и будем считать ее инерциальной. Под действием сил цилиндр совершает равномерное движение, уравнение которого имеет вид
mg + Q3 + Q4 + F = 0.
Для проекции на ось Ox: –fтр1 – fтр2 + F = 0.
Из симметрии задачи следует, что Q3 = Q4, тогда fтр1 = fтр2 и F = 2fтр. Если цилиндр скользит по плоскости желоба, то fтр = fmax = mN, где N – сила нормального давления.
Нормальная реакция опоры равна силе реакции Q1, которая действует на цилиндр, когда на него не действует сила F. Тогда, по 3-му закону Ньютона, Q1 = R1 = N, где R1 – сила давления цилиндра на плоскость (в данном случае R1 = N). Следовательно, fтр = mQ1.
Запишем условие равновесия цилиндра, когда на него не действует сила F: Q1 + Q2 + mg = 0,
и рассмотрим проекции на вертикальное направление. Угол между вертикалью и линией действия реакции опоры равен a (углы с взаимно перпендикулярными сторонами). Тогда
Проверка решения по размерности
С этой точки зрения задача решена верно, тогда
Задача 59. Куб из пенопласта с ребром a = 0,5 м, плывший по водоему, оказался зажатым под досками низкого горизонтального мостка. Какую горизонтальную силу необходимо приложить к кубу, чтобы сдвинуть его поступательно вдоль мостка? Плотность пенопласта rп = 60 кг/м3, плотность воды rв = = 103 кг/м3, высота мостка над уровнем воды h = 20 см, коэффициент трения между поверхностью куба и досками мостка m = 0,3.
Анализ условия
Куб взаимодействует со следующими телами: Землей, водой и мостком, а также с тем, кто проталкивает. Поэтому на него действуют четыре силы: сила тяжести mg, сила Архимеда FА, реакция мостка Q и сила F. На мосток действует сила R.
Так как между мостком и кубом существует трение, то при приложении силы F линия действия реакции Q отклоняется от вертикали таким образом, что ее горизонтальная составляющая уравновешивает силу F. Эта составляющая называется силой трения fтр. По мере увеличения силы F возрастает и сила трения, достигая при этом своего максимального значения – максимальной силы трения покоя fmax. В этом случае куб начинает двигаться.
Решение
Выберем систему отсчета, связанную с Землей, и будем считать ее инерциальной.
Когда куб начинает двигаться, то скорость его движения очень мала, и сопротивлением воды можно пренебречь, а само его движение считать равномерным. В этом случае приложенная сила F будет минимальной. Тогда уравнение движения куба выглядит следующим образом: mg + FA + Q + F = 0.
Спроектируем записанное векторное равенство на оси координат:
Ox: fmax – F = 0; (1)
Oy: –mg + FА – Qп = 0. (2)
По закону Кулона, максимальная сила трения покоя равна fmax = mN, где N – сила нормального давления, составляющая силы давления R по направлению, перпендикулярному поверхности соприкосновения тел.
По третьему закону Ньютона, Q = – R, или, для проекций на ось Oy, Qп = –(–N) = N.
Тогда, учитывая уравнение (2), получим fmax = mN = mQп = m(FА – mg).
Уравнение (1) примет вид: m(FА – mg) – F = 0.
Согласно закону Архимеда FА = rвVg, где V = a2(a – h) – объем вытесненной кубом воды.
Тогда F = m[rвa2(a – h)g – mg] = m[rвa2(a – h) – m]g.
Из определения плотности однородного тела m = rпVк = rпa3.
Окончательно получаем: F = m[rвa2(a – h) – rпa3]g = ma2[rв(a – h) – rпa]g; F = ma2[rв(a – h) – rпa]g.
Проверка решения по размерности
С этой точки зрения задача решена верно, тогда F = 0,3 • (0,5)2 [103(0,5 – 0,2) – 60 • 0,5] • 9,8 » 198 (Н).
Продолжение читаайте в № 34/01
