В УНИВЕРСИТЕТ!

Задачи, предлагавшиеся в разные годы при поступлении на естественные факультеты МГУ

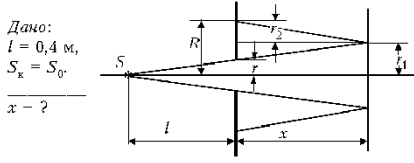
Задача 55. В непрозрачном экране вырезано небольшое круглое отверстие. Напротив центра отверстия, на расстоянии l = 0,4 м от него, помещен точечный источник света S. По другую сторону экрана находится плоское зеркало, причем плоскости зеркала и экрана параллельны. На каком расстоянии x от экрана расположено зеркало, если лучи, отраженные от зеркала, освещают на экране вокруг отверстия кольцо, площадь которого равна площади отверстия?

Анализ условия

Лучи света от точечного источника через небольшое отверстие прямолинейно распространяются до зеркала, где освещают круг радиусом r1. После отражения от зеркала они попадают на экран, высвечивая на нем кольцо радиусами R и r. [Для ясности можно продолжить крайние лучи за зеркало на расстояние x. – Ред.]

Решение

Из подобия получившихся треугольников найдем r1. Пусть радиус отверстия равен r, тогда:

Внешний радиус кольца R = r₁ + r₂. Из подобия треугольников найдем r₂:

Тогда:

Площадь кольца S_к = pR² – p r² = p (R² – r²), а площадь отверстия S₀ = p r². По условию задачи, они равны:

С учетом (2) получим:

.

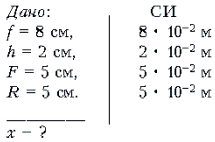
Задача 56. Действительное изображение светящейся точки получается на расстоянии f = 8 см от линзы и на расстоянии h = 2 см ниже ее главной оптической оси. На каком наименьшем расстоянии от линзы нужно поставить экран, имеющий форму верхней половины линзы, чтобы изображение точки исчезло? Фокусное расстояние линзы F = 5 см, ее радиус R = 5 см.

Анализ условия

В формировании изображения точки участвуют все лучи, проходящие через линзу. Если луч от точки не проходит через линзу, то она его не преломляет, и он не принимает участия в формировании изображения. Поэтому, чтобы изображение исчезло, нужно поставить экран таким образом, чтобы лучи не попадали на линзу. Расстояние между экраном и линзой будет наименьшим тогда, когда крайний луч проходит через нижнюю точку линзы.

Решение

Найдем расстояние d от линзы до светящейся точки, используя формулу линзы:

Все члены этой формулы входят в нее со знаком «плюс», т.к. фокус, изображение и предмет действительные. Отсюда:

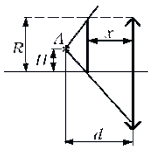Найдем расстояние H от светящейся точки до главной оптической оси линзы. Увеличение, даваемое линзой, равно:

Отсюда:

Рассматривая второй рисунок, из подобия треугольников получаем:

Тогда:

Подставляя (1) и (2) в (4), получим:

Продолжение читаайте в № 30/01