··· Решение задач: примеры, методы, приёмы ···

В.Г.ЭПШТЕЙН,
лицей «Профессионал», г. Харьков, Украина

itl967@online.kharkov.ua

Принцип развивающего обучения при изложении магнитных явлений

Известный принцип развивающего обучения предполагает такую организацию обучения, когда обучающийся не получает готовое знание, а «открывает» его в процессе собственной деятельности*. Разумеется, тем самым утверждается лишь направление совершенствования содержания. На пути реализации этого принципа в курсах естественнонаучных дисциплин и, в частности, в содержании курса физики, встречаются естественные трудности. Реальные научные открытия происходят в результате напряжённой (и длительной) деятельности выдающихся представителей рода человеческого. Поставить учащегося в такие условия, чтобы он мог самостоятельно пройти даже малую часть логического лабиринта научной картины мироздания, отнюдь не просто. Но там, где это удаётся, эффективность обучения значительно повышается. Ниже предложен именно такой способ изложения элементов разделов «Магнитное поле» и «Электромагнитная индукция», который позволяет реализовать идею развивающего обучения при максимально полном охвате основных идей электродинамики. Поводом для настоящей разработки явилось решение одной задачи из учебного пособия «Электродинамика-10–11» Г.Я.Мякишева и др. (М.: Дрофа, 1998).

Упражнение № 7, задача 11.

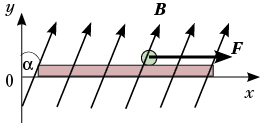
Прямоугольный контур ABCD, стороны которого имеют длины а и b, находится в однородном магнитном поле индукцией В и может вращаться вокруг оси ОО' (рис. 4.67). По контуру течёт ток I. Определите работу, совершённую магнитным полем при повороте контура на 180°, если вначале плоскость контура была перпендикулярна вектору индукции магнитного поля.

«Фокус» в том, что эта задача рассматривается в разделе «Магнитное поле»: мы «не имеем права» пользоваться формулой = –'. Разумеется, задачу можно решить и непосредственно – с использованием силы Лоренца, т.е. не выходя за рамки раздела. Это наводит на мысль о том, что оптимальный сценарий для представления «Магнетизма» в рамках школьной программы должен объединить раздел «Магнитное поле» с разделом «Электромагнитная индукция». Изложение можно построить в духе идей «развивающего обучения» – учащихся подводят к «открытию» закона электромагнитной индукции решением ряда задач.

Задача 1. Электромеханический преобразователь (идея электродвигателя)

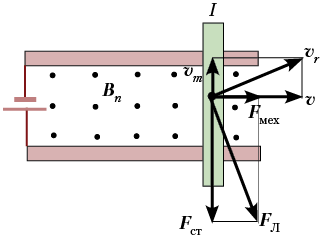
По горизонтальным рельсам может перемещаться металлический стержень длиной l, расположенный перпендикулярно рельсам. По стержню идёт ток I. Система находится в однородном магнитном поле В, составляющем угол с вертикалью. эдс источника . Сопротивлением источника и рельсов можно пренебречь. Сопротивление стержня R. Определите работу, совершаемую источником постоянного тока, и механическую работу при перемещении стержня на заданное расстояние a.

Качественный анализ

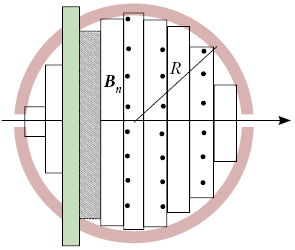
Заряд в движущемся проводнике с током перемещается вдоль проводника (со скоростью _m) и вместе с проводником (со скоростью проводника ). Это значит, что сила Лоренца F_Л, действующая на движущийся заряд в магнитном поле, имеет отличную от нуля составляющую вдоль стержня (F_ст – сторонняя сила) и поперёк него (F_мех). Составляющая F_мех совершает механическую работу. Составляющая F_ст препятствует движению заряда. Источник постоянного тока, таким образом, вынужден «продавливать» заряд через стержень, преодолевая действие указанной силы. При наличии электрического сопротивления стержня источник совершает также работу, преодолевая «трение». Работу, совершаемую источником по преодолению возникающего «сопротивления», и предлагается вычислить.

Вектор магнитной индукции направлен произвольно. Ясно, однако, что лишь компонента B_y определяет значение существенных параметров электромеханического преобразователя. Другие компоненты влияют на величины «поперечных» параметров (т.е. распределение заряда по сечению стержня) или не влияют вовсе. Условие задачи, таким образом, можно упростить, считая вектор B_n = B_y индукции параллельным оси Y. При этом B_n = B cos.

Количественный анализ

Механическая работа, совершаемая за промежуток времени t при перемещении заряда, есть A_мех = F_мех t, а поскольку компонента силы Лоренца F_мех = B_nq_m, то A_мех = B_nq_m t.

Работа другой составляющей за тот же промежуток времени есть A_ст = –F_{ст m} t (знак «–» появляется вследствие того, что сила направлена противоположно перемещению заряда), а поскольку компонента силы Лоренца F_ст = B_nq, то A_ст = –B_nq_mt.

Работа, совершаемая магнитным полем (работа cилы F_Л ), таким образом: А_Л = A_мех + A_ст= 0.

Итак, магнитное поле работу при перемещении заряда по проводнику не совершает (сила F_Л перпендикулярна скорости заряда _r).

Электрическое поле, создаваемое источником постоянного тока, «проталкивает» заряд по проводнику, преодолевая стороннюю силу. Сам движущийся проводник можно рассматривать при этом как источник постоянного тока, включённый навстречу «настоящему». Эдс этого источника легко вычислить: Эдс, как известно, совпадает с напряжением на концах разомкнутого источника (необходимо, таким образом, заменить неподвижный источник вольтметром, показания которого совпадают с Эдс). Работа сторонних сил, совершаемая этими силами при перемещении заряда по движущемуся проводнику, A_ст = –B_nql(_mt = l), а _инд = A_ст /q = – B_nl. Вольтметр (включённый вместо источника) и укажет расчётную величину Эдс, а замыкание цепи приведёт к возникновению электрического тока.

Итак, электромеханический преобразователь (двигатель) – устройство обратимое: электрический двигатель преобразуется в генератор электрического тока.

Какова же роль магнитного поля в работе преобразователя? Проведённый анализ демонстрирует: магнитное поле позволяет преобразовать энергию источника постоянного тока в механическую работу (и наоборот). Роль магнитного поля подобна роли шестерёнок в часовом механизме (источником энергии в котором является, например, сжатая пружина).

Энергетический анализ

Источник постоянного тока тратит энергию на преодоление сторонних сил и «сил трения». Математическая запись этого утверждения: U = = IR + B_nl, – представляет собой закон сохранения энергии для единичного положительного заряда, перемещаемого по цепи.

«Попутно» выясняется, что закон Ома для электромеханического преобразователя не выполняется. Связь тока и напряжения, даваемая законом Ома, – всего лишь частный случай вольт-амперной характеристики (проводника при постоянной температуре). Причём реализуется эта зависимость лишь в том случае, если иные каналы преобразования энергии электрического поля, кроме теплового, отсутствуют. Проясняется также различие между понятием «работа тока» (A = IUt) и законом Джоуля–Ленца (Q = I²Rt): IUt = I²Rt + B_nlIt.

Решение задачи

Поскольку, по условию, t = a, то работа, совершаемая источником при перемещении проводника:

A = I²Rt + B_nIla.

Очевидно, ответ при заданных условиях может быть получен лишь при значении R = 0:

A = B_nIla = A_мех.

Задача 2 (обобщение 1)

По горизонтальным рельсам, представляющим собой разрезанное кольцо радиусом R, может поступательно перемещаться металлический стержень. По стержню идёт ток I. Система находится в однородном магнитном поле B, составляющем угол с вертикалью. Определите механическую работу, которую совершает стержень при перемещении вдоль диаметра кольца, соединяющего точки разреза. Сопротивлением проводников пренебречь.

Решение.

Применим стандартный приём – сведём новую задачу к уже решённой (сведение сложного к простому). Задача легко сводится к предыдущей, если заменить окружность ломаной линией и рассмотреть движение проводника как последовательное перемещение по параллельным рельсам. Результат предыдущей задачи удобно представить в виде A = B_nIS, где A – работа на участке, а S – площадь участка.

Увеличение числа звеньев ломаной не меняет результат. В пределе (при увеличении количества звеньев до бесконечности) мы получаем:

A = A = B_nIS = B_nIR².

Решение задачи распространяется естественным образом на произвольный контур (форму рельсов) и произвольное (неоднородное) поле. Для такого обобщения удобно ввести новую величину – поток магнитного поля через поверхность, опирающуюся на замкнутый контур:

= _i = B_niS_i = Bcos_iS_i.

Тогда решение задачи записывается таким образом (назовём эту формулу правилом потока для вычисления работы): A = I , где – изменение потока через контур.

Как уже отмечалось, механическая работа, совершаемая при перемещении стержня, равна работе проекции силы Лоренца на направление тока в стержне (т.е. работе сторонних сил). Движущийся стержень превращается в источник постоянного тока («батарейку»), эдс которого можно вычислить:

(правило потока).

Задача 3 (обобщение 2)

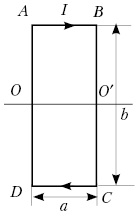
Прямоугольный контур, стороны которого имеют длины a и b, находится в однородном магнитном поле индукцией В и может вращаться вокруг оси ОО'. По контуру течёт ток I. Определите механическую работу, совершённую при повороте контура на 180°, если вначале плоскость контура была перпендикулярна вектору индукции магнитного поля.

Решение

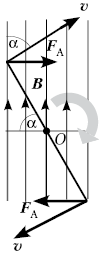
На стороны рамки AB и CD действуют силы Ампера, которые приводят рамку в движение. Вычислим работу этих сил: F_A = BIa.

Рассчитаем вначале работу сил Ампера A при малом повороте рамки на угол = ₂ – ₁:

A = 2 F_Asin · s

(учтена работа сил, действующих как на сторону AB, так и на сторону CD);

значит, A = BIa · b · sina · .

Согласно тригонометрическому соотношению с учётом малости поворота получим:

sin · = –(cos ₂ – cos ₁), откуда A = –BI · ab · (cos ₂ – cos ₁), а полная работа при повороте от ₀ до :

A = A = –BI · ab · (cos – cos ₀).

Учитывая определение потока, получаем:

A = – I · .

Сравнение полученной формулы с результатами уже решённых задач ставит проблему знака (в предыдущих результатах знака «–» не было). Этот вопрос решается знаком тока, который определяется совпадением или несовпадением с так называемым положительным направлением обхода контура – направлением вращения ручки буравчика, который вкручивают по вектору B. В данном случае I < 0,
< 0, значит, A > 0 (запись формул с использованием векторного произведения автоматически учитывает знаки всех величин).

Итак, с учётом знака тока, получаем A = I · . При этом, как и в ранее расмотренных ситуациях, работа сторонних сил A_ст = –I · . А это означает, что вращение контура в магнитном поле превращает его в «батарейку» с ЭДС и внешний источник «продавливает» ток, преодолевая сторонние силы.

Решение указанных задач позволяет сделать вывод, что генерируемая эдс зависит от изменения двух величин из трёх, входящих в определение потока (площади контура и угла между нормалью и направлением вектора магнитной индукции).

Возникает естественный вопрос: а не будет ли происходить генерация эдс при изменении третьей величины – индукции магнитного поля? Учащиеся вполне могут предложить опыты, направленные на проверку указанного предположения. Учитель, разумеется, должен приготовить «рояль в кустах» – необходимые приборы и материалы. Реализация этих опытов (опыты Фарадея) приводит к формулированию закона электромагнитной индукции.

Хотелось бы обратить внимание на реализацию в процессе изложения ещё одного принципа развивающего обучения – формирования целостного представления о предмете, что достигается:

– выяснением сущности закона Ома и закона Джоуля–Ленца (традиционное изложение создаёт, на мой взгляд, ложное представление об этих важных соотношениях);

– выяснением принципа действия электродвигателя и генератора как электромеханических преобразователей;

– выяснением роли магнитного поля в электромеханическом преобразователе;

– демонстрацией эффективного приёма решения задач – сведения общего к частному (сложного к простому);

– прояснением смысла понятия «работа» (разные силы выполняют «свою» работу);

– демонстрацией энергетического подхода к решению задач;

– прояснением смысла понятия ЭДС.

Предложенный «ход» позволяет логически объединить разделы магнетизма. Таким образом, решается задача построения более компактного, связного, ясного, эффективного изложения учебного материала.

____________________________________

*Петерсон Л.Г. Технология деятельностного метода как средство реализации современных целей образования. – М.: УМЦ «Школа 2000 …», 2004.

Вячеслав Григорьевич Эпштейн – учитель физики высшей квалификационной категории, методист, отличник образования Украины, Соросовский учитель (два гранта международного фонда «Возрождение»), преподаватель курсов повышения квалификации Института усовершенствования учителей, руководитель учебно-тренировочных сборов победителей областных олимпиад по физике, руководитель команды Харьковской области на Всеукраинской олимпиаде по физике. Автор большого количества публикаций на профессиональные темы в журналах Украины, СМИ, журнале «Квант» (2007, № 3), а вот теперь – и в газете «Физика (ПС)».