··· Приёмы и находки ···
1. Метод концептуальных схем
В настоящее время все педагоги отмечают повышенную невротизацию детей, а медицинские работники – ухудшение их физического здоровья. В чём причина этого? Можно ли поправить ситуацию? С одной стороны, статистики отмечают, что у родителей на первом месте по значимости стоит задача повышения социального статуса своего ребёнка, а здоровьесбережение – на шестом. С другой, школьная программа дошла до «невероятных высот»: выпускник должен овладеть 15 000 понятий, не считая терминов и иностранных слов. Не пора ли приостановить этот процесс бездумного расширения школьного материала?
Метод концептуальных схем, который применяю я, имеет давние корни, – ещё Л.А.Каменский в своей работе «Великая дидактика…» выводит правилом V, п. 19: «Всё, что подлежит изучению, пусть сперва предлагается в общем виде, а затем по частям». На собственном опыте я убедилась, что учебный материал надо подавать в концептуальной целостности, памятуя, что «целое больше суммы его частей». Законы психологии познания констатируют, что ребёнку необходимо создать общий образ изучаемого явления, а потом детализировать и углублять его*. Суть метода концептуальных схем, разработанного Ю.А.Самоненко, профессором МГУ им. М.В.Ломоносова, состоит в следующем:
– каждая концептуальная схема охватывает значительный раздел физики, представляющий достаточно цельную и законченную систему знаний, например: «Классическая механика», «Классическая термодинамика», «Классическая электродинамика» и пр.;
– концептуальная схема выявляет и предъявляет учащимся внутреннюю упорядоченную структуру рассматриваемой области, более или менее сложную, как правило, многоуровневую. Пример: три состояния вещества в термодинамике, три варианта движения зарядов (ускоренно, с постоянной и нулевой скоростью) в электродинамике;
– в основу концептуальной схемы положены системообразующие связи, например, третий закон Ньютона или закон сохранения энергии для механики, система уравнений Максвелла для электродинамики.
Таким образом, с введением концептуальной схемы мы в определённой степени по-новому начинаем применять хорошо известные принципы дидактики. Например, следуя принципу «от простого к сложному» мы всегда сначала изучали отдельные явления, а потом уже более сложные связи между ними. Применение концептуальной схемы предполагает вначале знакомство с предметом «в целом» (хотя и на элементарном уровне), а затем (и только при необходимости) углубление в тонкости отдельных явлений. Целостный взгляд на предмет и есть, по сути, то самое «простое», которое становится «сложным» в процессе углублённого, детального изучения.
Отметим ещё одну особенность. Сам принцип построения схемы и её использование при решении конкретных задач становится для учащегося самостоятельным предметом изучения и освоения. По сути, учащиеся овладевают системным анализом, не фиксируя его как специальный предмет изучения.
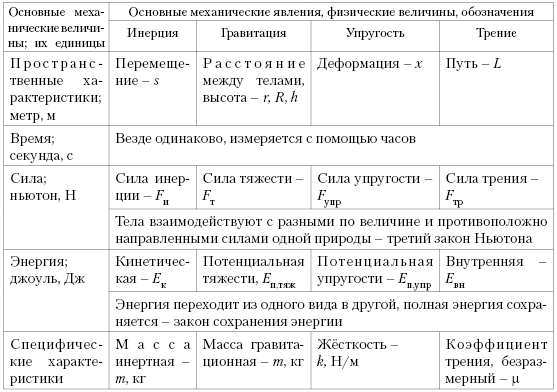
Итак, на первом этапе рассматриваются явления на качественном уровне. Каждому выдаётся табл. 1 (пустографка), наглядно показывающая не только предмет изучения выбранного раздела, например, классической механики, но и его внутреннюю структуру и связи. Учащиеся, опираясь только на эмпирические знания, заполняют левую колонку, создавая как бы «словесный портрет» изучаемого раздела. Завершением этапа является «физика без формул» – ученики решают разнообразные качественные задачи.
Таблица 1. Предмет изучения классической механики (качественный уровень)

Следующий этап включает работу с формулами, позволяющими проводить расчёты и получать количественные результаты (формулы здесь не показаны. – Ред.)
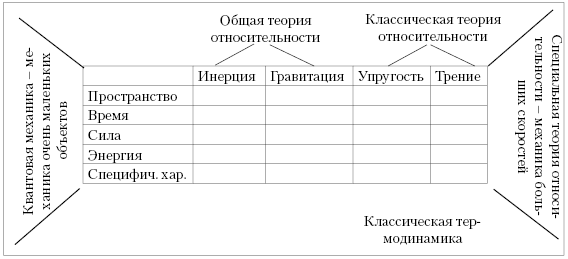
На третьем этапе концептуальная схема уточняется и дополняется, раскрываются метасистемные связи изучаемой области, табл. 2.
Таблица 2. Метасистемные связи раздела «Классическая механика»
Учащиеся с удовольствием переходят на новую систему отношений с предметом (и с учителем). Им интересно изучать материал самим (конечно, под руководством учителя), а не пассивно слушать (каким бы талантливым и живым ни было объяснение).
Описание каждого явления задаётся стандартно: вначале представляется качественная картина изменений характеристик явления, далее – их взаимосвязи и отношения в количественной форме. Качественное и количественное описания – два структурных уровня – обязательно присутствуют в схеме.
Оговариваются имеющие место идеализации и допущения. Концептуальная схема ориентирует учащихся в статусе изучаемых законов. Наглядный образ позволяет разъяснить, что экспериментальной основой механики являются силовые законы: второй закон Ньютона, закон всемирного тяготения, законы упругости и трения. Иной статус у третьего закона Ньютона и закона сохранения энергии – они не были открыты в конкретном эксперименте. Эти законы подтверждались во всех известных явлениях природы и в сфере деятельности человека, поэтому и были признаны всеобщими. Законы эти, связывая все явления между собой, являются, по сути, системообразующими связями, соединяющими отдельные элементы в цельную систему. Некоторые законы выводятся на основе других, более общих. Например, закон Архимеда можно получить из закона тяготения и закона Паскаля.
Концептуальная схема является основой для разработки учебных карт, определяющих содержание и способ овладения очередной порцией учебного материала. Обычно учебная карта составляется методистом или учителем. Задача учащегося – ориентироваться на её указания. В предлагаемой технологии обучения концептуальная схема позволяет самому учащемуся проявить интеллектуальную инициативу: составлять учебную карту, планировать собственную перспективу познавательных действий.
Ориентировка в предмете изучения отрабатывается с помощью специальных задач первоначально на качественном уровне. Эта часть программы, которую можно назвать «физикой без формул», очень важная для уяснения учеником «физического смысла» происходящих в механической системе изменений.
Обучение, изначально конструируемое на деятельностно-смысловой основе, может, с одной стороны, конкретно решать задачи образования, сформулированные ЮНЕСКО для XXI в. С другой, такого типа образование, над созданием которого мы работаем, способно служить экологии духовного, защите и сохранению творческого потенциала и тех, кто учится, и тех, кто учит.
Побуждение живого интереса к физике, уход от узкой специализации в процессе преподавания – всегда важнейшая задача для преподавателя в средней общеобразовательной школе. Диалогический метод позволяет показать физику в неповторимой красоте и доступности, т.к. отказ от монологической речи разнообразит методы познавательной деятельности учащихся. В процессе диалога учащиеся выступают на равных с преподавателем, и традиционно-дидактическое раскрытие материала переходит в новодидактическое, социально-психологическое общение. Во время диалога создаётся особая, комфортная атмосфера занятия, а постоянная обратная связь позволяет педагогу своевременно корректировать содержание исследуемого учебного материала. Несмотря на противоречие между управлением учебным процессом учителем и саморегулированием научения самим школьником, активизируется смысловая динамика и рождается потребность у ученика к самопониманию.
Учебный диалог позволяет получать развитие школьника как некоторый опыт пережитого знания. Чудо понимания окружающего мира даёт именно язык как механизм формирования опыта. В процессе диалога формируется умение обосновывать свои действия, навык задавать вопросы, т.е. дети осваивают и интериоризируют способы ведения дискуссии. Обращение заново к уже изученным явлениям с помощью обыденного языка и в ракурсе житейских представлений даёт возможность спровоцировать экстериоризацию спонтанных понятий учащихся и образовать разной степени сложности психологически связанных образов в сознании ребенка.
Сократический диалог даёт ещё одну интересную возможность: определённую незавершённость дискуссии, а значит, дополнительный стимул для самостоятельного осмысления проблемы учащимся.
Почему нужны специальные слова – термины
Преподаватель. Однажды я познакомился с мальчиком лет одиннадцати. Он очень плохо учился по математике, даже не мог поделить 90 на 2. Каково было моё удивление, когда я увидел его торгующим на базаре арбузами. Он работал быстро и чётко. Пришлось купить у него арбуз массой 3,5 кг по цене 17 рублей за килограмм. На мои 100 рублей этот мальчик мгновенно сдал 40 с половиной рублей. Почему 90 разделить на 2 трудно, а этот сложный расчёт был выполнен почти мгновенно?
Ученик. Цифры – это сложно, скучно, непонятно. А на деньгах понятнее.
Преподаватель. То есть в абстрактном виде делить и умножать трудно, а в обыденной жизни – легко. Наша задача – перестать бояться формул и научных слов. Постараться их понять и правильно применять. В каждой науке есть специальные слова – термины. Как вы думаете, зачем?
Ученик. Чтобы быстрее и точнее определять, о чём идёт речь.
Преподаватель. Например, я рассказываю о пружинном пистолете, говорю, как сильно сжата пружина. Какой физический термин подходит для описания состояния пружины?
Ученик. Явление упругости.
Преподаватель. А какую характеристику надо знать, чтобы понять, как сильно сжата пружина?
Ученик. Расстояние. То есть пространственную.
Преподаватель. Пришло время подробнее поговорить о пространстве. Как это понимать – пространство?
Ученик. Это место, где происходит явление, это размеры тела.
Преподаватель. На самом деле понятие пространства в физике углублялось и развивалось по мере проникновения в суть природных явлений. Под пространством мы понимаем прежде всего совокупность отношений и координацию объектов, т.е. их расположение относительно друг друга. Давайте придумаем задачу. Я начну, а вы продолжите: пришла информация, что вблизи станции Лианозово зарыт клад. Чтобы его найти, надо…
Ученик. Отсчитать от левого края платформы 148 шагов…
Преподаватель. Одну минутку, платформы две, определение «левая» тоже непонятно. Да и длина шагов может быть разная.
Ученик. Хорошо. От внешнего угла платформы в сторону Москвы пройти на восток 70 м.
Преподаватель. Пусть теперь продолжит кто-нибудь другой.
Ученик. Повернуть на юг и пройти 100 м...
Преподаватель. Хорошо. Следующий автор.
Ученик. Затем свернуть на запад и пройти 250 м.
Преподаватель. Достаточно. Какое расстояние в общей сложности будет пройдено?
Ученики. 70 + 100 + 250 = 420 м.
Преподаватель. За какое время можно пройти этот путь?
Ученик. Минут за 20–25.
Преподаватель. А нет ли у этой задачи другого решения?
Ученик. Можно сначала нарисовать, а потом выбрать маршрут, – он может оказаться короче.
Преподаватель. Что для этого понадобится?
Ученик. Надо учесть стороны света и масштаб – и можно существенно сократить путь.

Преподаватель. Конечно. Вот какие результаты даёт грамотное умение складывать векторы. Подытожим, что даёт научный подход в решении самых неожиданных задач?
Ученик. Возможность действовать в разных ситуациях быстрее и результативнее.

Людмила Николаевна Рагулина – учитель физики высшей квалификационной категории, окончила физико-математический факультет ЛГПИ им. А.И.Герцена в 1976 г. Людмила Николаевна – отличник народного образования, победитель всероссийского конкурса «Лучшие учителя России». Имеет публикации в сборнике «Ломоносовские чтения», «Практическом журнале для администрации и учителя» и др.
_________________________________
*Есть и другие подходы: детям, обладающим дифференциальным когнитивным стилем мышления, рекомендуется сначала давать частности, а уже потом объединять их, интегрировать. Таких детей примерно четверть. См., например, дистанционный курс 16-007 О.В.Коршуновой «Учёт особенностей мышления учащихся при обучении физике (интегративно-дифференцированный подход). – Ред.