Количественный анализ простейших сплавов

Урок закрепления знаний, 7-й класс

Тела более тяжёлые, чем жидкость, опущенные в эту жидкость,
будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче
на величину веса жидкости в объёме, равном объёму погружённого тела.

Архимед. Сочинения (М., 1962)

Цель урока: вторичное закрепление усвоенных знаний, выработка умений по их применению.

Дидактическая задача: установление правильности и осознанности усвоения нового учебного материала.

Рефлексивная деятельность ученика: самоосмысление, самовыражение и самоутверждение.

Деятельность учителя по обеспечению рефлексии: определение зоны ближайшего и актуального развития.

Показатели реального результата решения задачи: усвоение сущности новых знаний и способов действий на репродуктивном уровне.

Логика построения урока: актуализация ведущих способов и действий – восприятие образца применения знаний – самостоятельное применение знаний в сходной ситуации.

Теоретическое обоснование

Рассматривая экспериментальные задания различного типа, в которых ученики определяют какие-либо неизвестные физические параметры тела или системы (объём, массу, плотность и т.д.), небезынтересно остановиться на тех задачах, решение которых связано с использованием понятий «концентрация» и «процентное содержание» (обычно в условиях речь идёт о составлении сплавов, растворов или смесей двух или нескольких веществ). Основные допущения, как правило, принимаемые в задачах подобного рода, состоят в следующем [1]:

– все получающиеся сплавы или смеси однородны;

– при слиянии двух растворов, имеющих объёмы V₁ и V₂, получается смесь, объём которой равен сумме объёмов компонент: V₀ = V₁ + V₂ (последнее соотношение не всегда выполняется в действительности – при слиянии двух растворов сохраняется не объём, а масса смеси).

Рассмотрим для определённости смесь двух компонент А и В. Объём смеси V₀ = V_A + V_B, а два отношения – – показывают, какую долю полного объёма смеси составляют объёмы отдельных компонент: V_A = C_AV₀, V_B = C_BV₀.

Отношение объёма чистой компоненты в растворе ко всему объёму смеси называется объёмной концентрацией этой компоненты.

Концентрация – это безразмерная величина; сумма концентраций всех компонент, составляющих смесь, очевидно, равна единице: С_А + С_В = 1. Поэтому для того, чтобы структура раствора, состоящего из n компонент, была определена, достаточно знать концентрацию (n – 1) компонент.

Очевидно, что V₀ = C_AV₀ + C_BV₀ + ... + C_nV₀.

Объёмным процентным содержанием компоненты А называется величина р_A = С_А · 100%, т.е. концентрация этого вещества, выраженная в процентах. По известной С_А находится концентрация компоненты А: Например, если процентное содержание составляет 70%, то соответствующая концентрация равна 0,7. Процентному содержанию 10% соответствует концентрация 0,1 и т.д.

Таким же способом определяются массовая концентрация и массовое процентное содержание, а именно как отношение массы чистого вещества А в смеси к массе всей смеси. О какой концентрации, объёмной или массовой, идёт речь в конкретной задаче, всегда ясно из её условия.

Встречается ряд задач, в которых приходится пересчитывать объёмную концентрацию в массовую и наоборот. Чтобы это сделать, необходимо знать плотности компонент, составляющих смесь, раствор или сплав. Рассмотрим для примера двухкомпонентную смесь с объёмными концентрациями компонент C₁ и C₂ (C₁ + C₂ = 1) и плотностями компонент соответственно ₁ и ₂. Массу смеси можно найти по формуле m = V₁₁ + V₂₂, в которой V₁ и V₂ – объёмы составляющих смесь компонент. Массовые концентрации компонент находят из равенств:

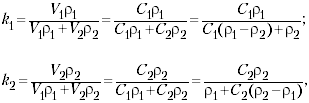
которые определяют связь этих величин с объёмными концентрациями.

Приборы и материалы: динамометр, штатив с муфтой и лапкой, стакан с водой, весы с разновесами, измерительный цилиндр (мензурка), нитки, латунный цилиндр из набора тел для калориметра.

Ход урока

Вариант I. Урок проводится после выполнения учащимися фронтальной лабораторной работы № 7 «Определение выталкивающей силы, действующей на погружённое в жидкость тело» [2, с. 167].

1. Решение вместе с учителем основополагающей установочной задачи [3, № 8.12, с. 81]* (10 мин)

Сплав из золота и серебра массой 13 кг 410 г при полном погружении в воду стал весить 125,10 Н. Определите количество золота и серебра в сплаве, если известно, что плотность золота 19,3 г/см³, а серебра 10,5 г/см³.

Решение [3, № 8.12, с. 86]. Сплав в воздухе весил 134,1 Н, следовательно, при погружении в воду он потерял в весе 9Н, т.е., по закону Архимеда, столько же весит вытесненная им вода. Следовательно, объём сплава равен 900 см³, а плотность 134,1/900 = 14,9 г/см³. Пользуясь старинным способом (см. ниже), получаем схему

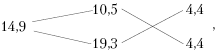
из которой следует, что объёмы золота и серебра в сплаве находятся в отношении 4,4 : 4,4, значит, просто равны друг другу.

Замечание. Суть старинного способа заключается в следующем [3, № 8.3, с. 83]. Пусть требуется смешать растворы a-процентной и b-процентной кислоты, чтобы получить c-процентный раствор. Без ограничения общности можно считать, что a < b, причём a c b: если c < a или c > b, то c-процентный раствор, конечно, получить нельзя. Пусть мы смешиваем x граммов раствора a-процентной и y граммов раствора b-процентной кислот. Тогда в первом растворе содержится ax/100 г чистой кислоты, а во втором by/100  г.

В полученной смеси массой (x + y) г будет содержаться чистой кислоты, что должно составлять Таким образом, должно быть выполнено равенство откуда вытекает соотношение (b – c)y = (c – a)x, т.е.

Такой же вывод даёт схема

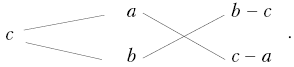
Изложение старинного способа целесообразно провести ранее, при изучении явления диффузии, закрепив теоретический материал решением соответствующих задач [3, с. 78–89].

Заметим также, что при решении установочной задачи старинный способ применялся в несколько необычной ситуации: количества смешиваемых веществ измерялись их объёмами, а роль концентрации играла плотность (полезно убедиться, что схема по-прежнему применима).

2. Самостоятельные измерения и расчёты учащихся применительно к латуни при координирующей и контролирующей роли учителя (25 мин)

Используя выводы, полученные при решении установочной задачи и упрощённо считая латунь сплавом меди и цинка [4, с. 1488], имеем:

– F₁ = 1,7 Н – показания динамометра с подвешенным к нему латунным цилиндром в воздухе;

– F₂ = 1,5 Н – то же, при полном погружении цилиндра в воду;

– F = 1,7 Н – 1,5 Н = 0,2 Н – разность показаний динамометра;

– – масса вытесненной цилиндром воды;

– – объём вытесненной цилиндром воды, равный объёму сплава;

– – масса латунного цилиндра;

– – плотность сплава.

Согласно таблице № 2 [2, с. 50, 51], плотности меди и цинка равны соответственно 8,9 г/см³ и 7,1 г/см³.

Используя старинный способ, получаем схему:

из которой следует, что объёмы меди V₁ и цинка V₂ находятся в сплаве в отношении 7 : 2, т.е. справедливо приближённое равенство V₁ = 3,5V₂.

Далее: V = V₁ + V₂ = 3,5V₂ + V₂ = 4,5V₂.

Отсюда:

–

– V₁ = V – V₂ = 20 см³ – 4,4 см³ = 15,6 см³;

– – объёмная концентрация меди;

– C₂ = 1 – C₁ = 1 – 0,78 = 0,22 – объёмная концентрация цинка;

– p₁ = C₁ · 100% = 0,78 · 100% = 78% – объёмное процентное содержание меди;

– p₂ = C₂ · 100% = 0,722 · 100% = 22% – объёмное процентное содержание цинка;

– m₁ = ₁ · V₁ = 8,9 г/см³ · 15,6 см³ = 138,84 г – масса меди в латунном цилиндре;

– m₂ = m – m₁ = 170 г – 138,84 г = 31,16 г – масса цинка в в латунном цилиндре;

– – массовая концентрация меди;

– k₂ = 1 – k₁ = 1 – 0,82 = 0,18 – массовая концентрация цинка.

В качестве абсолютной погрешности измерения, согласно [5], следует принять погрешность отсчёта, которая не превосходит половины цены деления динамометра, т.е.

Относительная погрешность измерений равна

т.е. _F = 6%.

3. Заполнение итоговой таблицы результатов измерений и вычислений. Замечания и выводы по уроку (5 мин)

Содержание таблицы очевидно, т.к. должно включать в себя все измеренные, рассчитанные и справочные величины, а также погрешности измерений. Форму таблицы учащиеся выбирают самостоятельно.

Вариант II. Урок проводится после выполнения учащимися фронтальной лабораторной работы № 5 «Определение плотности вещества твёрдого тела» [2, с. 164, 165]. Рассчитывается плотность латуни, строится схема старинного способа. Дальнейшие действия полностью повторяют вариант I. (При отсутствии необходимого оборудования схема старинного способа строится на основе данных таблицы № 2 [2, с. 50, 51]. Измерения не проводятся. Заметим также, что содержание установочной задачи должно быть изменено, т.к. учащиеся ещё не ознакомлены с понятием выталкивающей силы. Необходимые поправки несложно сделать самостоятельно.)

Вариант III. Сводится к измерению согласно инструкциям к фронтальным лабораторным работам № 3 «Измерение массы тела на рычажных весах» [2, с. 161–163] и № 4 «Измерение объёма тела» [2, с. 163, 164], измерениям массы и объёма латунного цилиндра и последующему решению системы двух линейных уравнений:

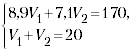
(смысл обозначений и численных коэффициентов см. выше).

Необходимость в схеме старинного способа и решении установочной задачи при этом отпадает. Основная трудность заключается в том, что на момент изучения понятий массы, объёма, плотности школьники не владеют понятием линейного уравнения, не умеют решать их системы. Учителю физики приходится либо вводить эти понятия самому, бегло и нестрого, либо проводить работу в конце учебного года на уроках обобщения и повторения или за счёт резерва учебного времени. Излишне говорить, что после решения указанной выше системы дальнейший расчёт проводится в полном соответствии с вариантом I.

Литература

1. Лурье М.В., Александров Б.И. Задачи на составление уравнений: Учеб. руководство. – М.: Наука, 1990, с. 5–7.

2. Пёрышкин А.В. Физика-7: Учеб. для общеобразоват. учеб. заведений. – М.: Дрофа, 2002.

3. Сергеев И.К., Олехник С.Н., Гашков С.Б. Примени математику. – М.: Наука, 1990.

4. Учебный справочник школьника. – М.: Дрофа, 1999.

5. Физический практикум для классов с углублённым изучением физики: Дидакт. материал: 9–11 кл.: Под ред. Ю.И.Дика, О.Ф.Кабардина. – М.: Просвещение, 1993, с. 10.

__________________________

*Мы сделали поправки в текстах условий и решений в соответствии с принятыми в СИ единицами массы и веса, приняв ускорение свободного падения g = 10 м/с². – Ред.