Продолжение. См. № 8/07
I. МЕХАНИКА (продолжение)
6
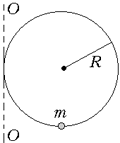На жёсткое кольцо радиусом R из тонкой
проволоки, плоскость которого вертикальна,
надета маленькая бусинка m так, что она
располагается в нижней точке кольца. Кольцо
начинают медленно раскручивать вокруг
вертикальной оси ОО, показанной на рисунке.
Найти коэффициент трения 
бусинки о проволоку, если при угловой
скорости вращения кольца 
бусинка поднялась на высоту h = 0,5 R.
Решение
Будем считать, что ось ОО
неподвижна относительно лабораторной системы
отсчета и эта система является инерциальной.
Кроме того, будем считать, что на бусинку
действуют только сила тяжести mg,
направленная вертикально вниз, и сила реакции
кольца. Эту силу, как обычно, представим в виде
суммы нормальной составляющей N,
направленной по радиусу кольца к его центру, и
направленной по касательной к кольцу силы сухого
трения Fтр. Согласно закону
Кулона–Амонтона, максимальное значение силы
сухого трения покоя по модулю равно N. Будем считать, что
модуль силы сухого трения скольжения равен
модулю максимальной силы сухого трения покоя.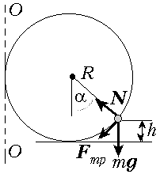
Как видно из рисунка, поднявшаяся на
высоту h бусинка движется по окружности
радиусом R(1 + sin
), где cos = 1 – h/R. По условию задачи при этом
угловая скорость бусинки равна . Учитывая, что кольцо
раскручивают медленно, можно пренебречь
тангенциальной составляющей ускорения бусинки и
на основании второго закона Ньютона утверждать,
что
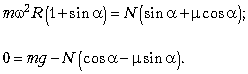
Учитывая, что по условию задачи, cos = 0,5, а потому 
из предыдущих
уравнений получаем, что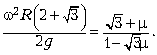 
Решая это уравнение, находим искомое значение коэффициента трения
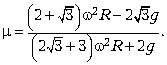
Следует отметить, что полученное
решение верно (т.е.
> 0), если 
Если
же это условие не выполняется, то задача не имеет
решения.