В.С.СТЕПАНОВА,
Н.И.ЧИСТЯКОВА, А.А.ЯКУТА В.С.СТЕПАНОВА,
Н.И.ЧИСТЯКОВА, А.А.ЯКУТА Продолжение. См. № 11/06
I. МЕХАНИКА (окончание)
4 В системе,
показанной на рисунке, трения между бруском
массой m = 1 кг и наклонной поверхностью клина
нет.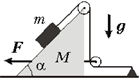 
Коэффициент трения клина о
горизонтальную плоскость равен 
= 0,1. Масса клина с блоками М
= 10 кг. Угол при основании клина 
= 45°. Нить гладкая, невесомая,
нерастяжимая, а её участок, прикреплённый к
бруску, параллелен поверхности клина. Другой
конец нити закреплён так, что нижний отрезок нити
горизонтален. К клину прикладывают
горизонтальную силу F,
направленную так, как показано на рисунке. При
этом клин движется поступательно с постоянной
скоростью в направлении силы F.
Найти модуль силы F.
Решение
Будем считать, что горизонтальная плоскость, по которой скользит клин, неподвижна относительно лабораторной системы отсчёта XOY, и эта система является инерциальной.
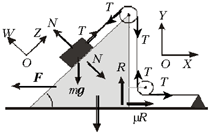
По условию задачи, нить является гладкой. Поэтому со стороны блоков на нить могут действовать только силы, направленные по нормалям к границам соприкосновения нити с блоками. Из сказанного, с учётом невесомости нити, следует, что модуль Т силы натяжения во всех точках нити одинаков. Поэтому можно утверждать, что на блоки со стороны нити действуюдействуют силы, сумму которых можно представить в виде двух составляющих, показанных на рисунке стрелками, рядом с которыми указаны их модули, равные Т.
На этом же рисунке изображены силы тяжести mg и Mg, действующие на брусок и на клин. Здесь же с учётом третьего закона Ньютона показаны и силы реакции клина на брусок и бруска на клин. Поскольку между бруском и клином нет трения, эти силы реакции направлены по нормали к границе соприкосновения бруска и клина. Модули этих сил на рисунке обозначены символом N.
Сила реакции плоскости на клин
показана, как обычно, в виде двух составляющих:
нормальной, модуль которой равен R, и
тангенциальной, часто называемой силой сухого
трения. По условию задачи, клин движется
поступательно в направлении приложенной к нему
горизонтальной силы F. Поэтому сила
трения направлена противоположно силе F.
Считая силу сухого трения скольжения равной
максимальному значению силы сухого трения покоя,
эту составляющую силы реакции плоскости на клин
мы изобразили на рисунке стрелкой, под которой
указан её модуль R.
По условию задачи, клин движется поступательно и равномерно. Поэтому уравнение движения клина в проекциях на оси XOY можно представить в виде:
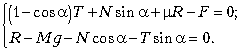(1)
Система отсчёта ZOW, неподвижная относительно клина, будет инерциальной.
По условию задачи, отрезок нити между бруском и точкой касания верхнего блока параллелен наклонной плоскости клина. Нижний отрезок нити горизонтален. Длина всей нити постоянна. Поэтому брусок будет двигаться по клину равномерно, т.к. клин, по условию задачи, движется поступательно с постоянной скоростью в направлении силы F. Следовательно, уравнения движения бруска в проекциях на оси системы ZOW будут иметь вид:
(2)
Решая совместно cистему уравнений (1) и (2), находим модуль силы F:
5 По
плоскости, образующей с горизонтом угол , без
проскальзывания катится цилиндрическая
тонкостенная бочка массой m, заполненная
жидкостью массой М. При этом направление оси
бочки остаётся неизменным и горизонтальным.
Пренебрегая массой днищ и трением между стенками
бочки и жидкостью, найти модуль а ускорения
оси бочки.
Решение
Будем решать задачу, считая, что выполнены следующие стандартные предположения: лабораторная система отсчёта, относительно которой покоится наклонная плоскость, является инерциальной; воздух не оказывает никакого влияния на скатывающуюся бочку; силами трения качения, действующими на бочку, можно пренебречь. Кроме того, будем считать бочку твёрдым телом, цилиндрическая часть которого изготовлена из однородного материала, а жидкость несжимаемой.
По условию задачи, силами трения жидкости о бочку следует пренебречь. Поэтому при скатывании бочки жидкость будет оставаться неподвижной относительно её оси. Поскольку жидкость мы считаем несжимаемой и, по условию задачи, ось бочки при её скатывании не изменяет своего направления в пространстве, то скорости и ускорения всех частиц жидкости нужно считать равными соответствующим величинам для оси бочки.
Решить задачу, составив уравнения движения бочки и жидкости, не представляется возможным, т.к. программа вступительных испытаний по физике в МГУ не предусматривает знания абитуриентами уравнения вращательного движения тел. Вместе с тем, решение задачи можно получить, используя закон сохранения механической энергии. Действительно, при выполнении сделанных предположений механическую систему, состоящую из жидкости, бочки и Земли с закреплённой на ней наклонной плоскостью, по которой скатывается бочка, можно считать изолированной консервативной системой. Утверждая это, мы учли, что между бочкой и плоскостью действуют силы трения покоя, т.к., по условию задачи, бочка скатывается без проскальзывания. Хотя именно эти силы обеспечивают ускоренное вращение бочки вокруг своей оси, их суммарная работа над бочкой и плоскостью равна нулю. Поэтому указанную механическую систему при выполнении ранее сделанных предположений о влиянии воздуха и силах трения качения можно считать консервативной.
Пусть к некоторому моменту времени t
после начала скатывания скорость оси бочки в
выбранной системе отсчёта стала равной 
. Следовательно,
кинетическая энергия жидкости к этому моменту
времени стала равной Wкж = 0,5M
2.
Чтобы вычислить кинетическую энергию
бочки, когда её ось движется со скоростью , учтём, что
массой днищ, по условию задачи, можно пренебречь,
а все точки её цилиндрической части в системе
отсчёта, движущейся поступательно вместе с осью
бочки, имеют одинаковые по модулю скорости, т.к.
эта часть является тонкостенной. Поскольку бочка
скатывается без проскальзывания, её угловая
скорость вращения 
= /R, где R
– радиус цилиндрической части бочки, а = ||. Отсюда следует, что скорость любой i-й
точки этой части в выбранной лабораторной
системе отсчёта равна i = + iвр,
где вектор iвр
– скорость i-й точки относительно оси бочки.
Поскольку кинетическая энергия совокупности
точек равна сумме их кинетических энергий, то
кинетическая энергия рассматриваемой бочки,
катящейся со скоростью , равна
При вычислении кинетической энергии
бочки было учтено, что |iвр| = R = , массы
диаметрально противоположных точек
цилиндрической поверх-ности бочки равны, т.к., по
предположению, эта часть изготовлена из
однородного материала, а скорости этих точек
относительно оси бочки равны по величине, но
противоположны по направлению.
Таким образом, к тому моменту, когда
скорость оси бочки стала равной , кинетическая энергия бочки
с жидкостью стала равной Wк = (m + 0,5M)2. Поскольку
масса Земли на много порядков превышает массу
бочки с жидкостью, изменением кинетической
энергии Земли при скатывании бочки следует
пренебречь. Именно поэтому лабораторную систему
отсчёта следует считать инерциальной, а
кинетическую энергию рассматриваемой
механической системы – равной Wк.
Через столь малый промежуток времени 
t, в течение
которого ускорение оси бочки можно считать
неизменным и равным a, модуль её
скорости увеличится на = at. При этом
кинетическая энергия системы увеличится на
Это приближённое равенство при t 
0 становится точным, т.к. при
этом / = at/ 0. За время t ось бочки переместится
вдоль наклонной плоскости на расстояние L = ( + 0,5at)t 
t, опустившись по вертикали
вниз на h = Lsin. Следовательно, за это время
потенциальная энергия рассматриваемой
механической системы уменьшится на величину Wп = (m
+ M)gLsin, где g – модуль
ускорения свободного падения.
Поскольку наша механическая система,
как было показано выше, может считаться
изолированной консервативной, то должно
выполняться условие: Wп = Wк, т.е. (m + M)gtsin = (2m + M). Из этого равенства
следует, что модуль ускорения а, равный при
прямолинейном движении /t при t 0, при выполнении сделанных
предположений должен оставаться неизменным при
скатывании бочки и быть равным:
