Окончание. См. № 11/07
В задачах третьего типа составляем импульсно-энергетическую систему уравнений. Одно уравнение – на закон сохранения импульса, другое – на закон сохранения энергии. Как правило, сюжетом таких задач является удар тел.
Задача 5. Тело массой m,
движущееся со скоростью ![]() ,
налетает на покоящееся второе тело и после
упругого столкновения отскакивает от него под
углом 90° к первоначальному направлению движения
со скоростью
,
налетает на покоящееся второе тело и после
упругого столкновения отскакивает от него под
углом 90° к первоначальному направлению движения
со скоростью ![]() Определите массу M второго тела.
Определите массу M второго тела.
Решение.
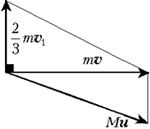
Пусть u – скорость второго тела после удара. Тогда имеем систему уравнений:
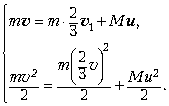
Вектор ![]() а
а ![]() 1 =
1 = ![]() . Первому векторному уравнению
соответствует рисунок. По теореме Пифагора:
. Первому векторному уравнению
соответствует рисунок. По теореме Пифагора:
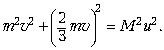
Скалярная система уравнений
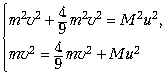
легко упрощается:
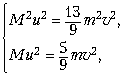
откуда сразу вытекает: M = 2,6m.
В следующей задаче удар будет бесконтактным.
Задача 6. Два электрона
находятся на бесконечно большом расстоянии друг
от друга, причём первый электрон покоится, а
второй летит на него со скоростью ![]() 0. Определите наименьшее расстояние,
на которое они сблизятся.
0. Определите наименьшее расстояние,
на которое они сблизятся.
Решение.
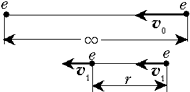
Физически ясно, что второй электрон будет тормозиться кулоновской силой, а первый – ею же разгоняться. При сближении электронов на наименьшее расстояние r их скорости сравняются, т.е. относительная скорость электронов обратится в нуль. В дальнейшем первый электрон начнёт удаляться от второго. По законам сохранения энергии и импульса, имеем систему уравнений:
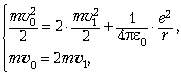
где m и e – масса и заряд
электрона соответственно. Из второго уравнения
сразу получается: ![]() тогда первое уравнение даёт:
тогда первое уравнение даёт: ![]()
Рассмотрим, наконец, отдельные физически интересные задачи, не укладывающиеся в таблицу. Так, для решения следующей задачи необходимо и достаточно применить только один закон сохранения импульса.
Задача 7. (МФТИ, 1991.) После
разрыва неподвижного снаряда образовалось
четыре осколка. Осколок массой m1 = 4 кг
полетел вертикально вниз со скоростью ![]() 1 = 150 м/с, осколок
массой m2 = 3 кг – горизонтально
на юг со скоростью
1 = 150 м/с, осколок
массой m2 = 3 кг – горизонтально
на юг со скоростью ![]() 2 = 100 м/с,
осколок массой m3 = 1 кг –
горизонтально на восток, осколок массой m4 =
4 кг – со скоростью
2 = 100 м/с,
осколок массой m3 = 1 кг –
горизонтально на восток, осколок массой m4 =
4 кг – со скоростью ![]() 4 = 200 м/с.
Найдите скорость третьего осколка.
4 = 200 м/с.
Найдите скорость третьего осколка.
Решение.
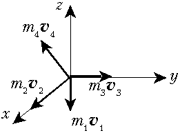
Так как снаряд был первоначально
неподвижным, то, по закону сохранения импульса,
верно равенство
m1![]() 1 +
m2
1 +
m2![]() 2 + m3
2 + m3![]() 3 + m4
3 + m4![]() 4 = 0. Заметим, что
векторы m1
4 = 0. Заметим, что
векторы m1![]() 1,
m2
1,
m2![]() 2, m3
2, m3![]() 3 взаимно
перпендикулярны. Поэтому преобразуем наше
равенство и возведём его в квадрат, учитывая, что
скалярный квадрат вектора равен квадрату его
модуля:
3 взаимно
перпендикулярны. Поэтому преобразуем наше
равенство и возведём его в квадрат, учитывая, что
скалярный квадрат вектора равен квадрату его
модуля:
![]()
откуда находим:
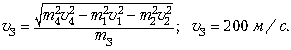
Когда движется не материальная точка, а протяжённое тело, то в зависимости от того, какая величина является неизвестной, часто бывает достаточно одного энергетического уравнения.
Задача 8.
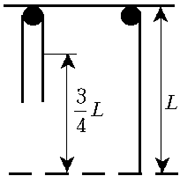
Канат длиной L переброшен через
штырь. В начальный момент концы каната
находились на одном уровне. После слабого толчка
канат пришёл в движение. Определите скорость ![]() каната к моменту, когда он
соскользнёт со штыря. Трением пренебречь.
каната к моменту, когда он
соскользнёт со штыря. Трением пренебречь.
Решение. Пусть масса каната m.
Потенциальную энергию отсчитываем от нулевого
уровня, обозначенного пунктиром. Учитываем, что в
формуле потенциальной энергии mgh под
высотой h надо понимать высоту центра
тяжести тела. Поскольку все точки каната
движутся с одной и той же скоростью, его
кинетическую энергию определяем как ![]() Из закона сохранения
энергии приходим к уравнению
Из закона сохранения
энергии приходим к уравнению
![]()
откуда искомая скорость ![]()
В заключение приведём ряд конкурсных задач для самостоятельного решения с ответами.
Задача 1. (Физфак МГУ им.
М.В.Ломоносова, 1974.) Космический корабль
находится на расстоянии h = 20 000 км
от поверхности Земли и в системе координат,
связанной с Землёй, имеет скорость ![]() 1 = 6 км/с, направленную
по радиусу от центра Земли. Двигатели не
работают. Упадёт ли корабль на Землю или улетит в
космическое пространство? Что произойдёт при тех
же условиях, если скорость корабля 5 км/с?
4 км/с?
1 = 6 км/с, направленную
по радиусу от центра Земли. Двигатели не
работают. Упадёт ли корабль на Землю или улетит в
космическое пространство? Что произойдёт при тех
же условиях, если скорость корабля 5 км/с?
4 км/с?
Ответ. Улетит; упадёт; упадёт.
Задача 2. (Физфак МГУ им.
М.В.Ломоносова, 1979.) С каким ускорением будут
двигаться по наклонной плоскости два жёстко
скреплённых между собой тела, имеющие массы m1
и m2? Коэффициенты трения между телами
и наклонной плоскостью равны соответственно k1
и k2. Угол наклонной плоскости равен ![]() .
.
Ответ. 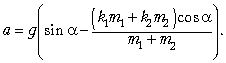
Задача 3. (Физфак МГУ им. М.В.Ломоносова, 1981.) Невесомая платформа укреплена, как на ножках, на четырёх одинаковых невесомых пружинах. С высоты H падает тело массой m и, попав точно в середину платформы, прилипает к ней. Чему равна амплитуда возникших при этом колебаний, если жёсткость каждой пружины k?
Ответ. 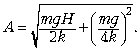
Задача 4. (Физфак МГУ им.
М.В.Ломоносова, 1989.) Двигатель запускаемого с
Земли реактивного снаряда массой m работает
время ![]() , создавая
постоянную по величине и направлению силу тяги F
и обеспечивая прямолинейное движение снаряда
под углом
, создавая
постоянную по величине и направлению силу тяги F
и обеспечивая прямолинейное движение снаряда
под углом ![]() к
горизонту. Определите высоту, на которой
прекращается работа двигателя. Изменением массы
снаряда и сопротивлением воздуха пренебречь.
к
горизонту. Определите высоту, на которой
прекращается работа двигателя. Изменением массы
снаряда и сопротивлением воздуха пренебречь.
Ответ. 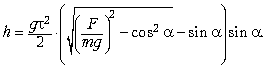
Задача 5. (Физфак МГУ им. М.В.Ломоносова,
1994.) На наклонную плоскость положили шайбу и
сообщили ей скорость, направленную вдоль
плоскости вверх. Коэффициент трения шайбы о
плоскость равен ![]() .
Найдите угол наклона плоскости к горизонту, при
котором шайба пройдёт минимальное расстояние до
остановки.
.
Найдите угол наклона плоскости к горизонту, при
котором шайба пройдёт минимальное расстояние до
остановки.
Ответ. ![]()
Задача 6. За какое время t
тело соскользнёт с наклонной плоскости высотой h,
наклонённой под углом ![]() к горизонту, если по наклонной
плоскости с углом наклона
к горизонту, если по наклонной
плоскости с углом наклона ![]() оно движется равномерно?
оно движется равномерно?
Ответ. 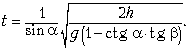
Задача 7. Нить с подвешенным
на ней грузом отклонили на угол ![]() и отпустили. На какой угол
и отпустили. На какой угол ![]() отклонится нить с
грузом, если при своём движении она будет
задержана штифтом, поставленным под точкой
подвеса на середине длины нити?
отклонится нить с
грузом, если при своём движении она будет
задержана штифтом, поставленным под точкой
подвеса на середине длины нити?
Ответ. ![]()
Задача 8. С горы высотой h = 2 м и основанием b = 5 м съезжают санки, которые затем останавливаются, пройдя по горизонтали путь l = 35 м от основания горы. Найдите коэффициент трения, считая, что он одинаков на наклонной плоскости и на горизонтали. Переход с горы на горизонталь санки проходят без трения.
Ответ. ![]() k = 0,05.
k = 0,05.
Задача 9. Груз массой m = 0,2 кг, подвешенный на пружине жёсткостью k = 20 Н/м, лежит на подставке так, что пружина не деформирована. Подставку резко убирают, и груз начинает двигаться. Найдите его максимальную скорость.
Ответ. ![]()
Задача 10. Частица кинетической энергией E0 упруго сталкивается с такой же неподвижной частицей и отклоняется от первоначального направления на угол 60°. Определите кинетические энергии частиц после соударения.
Ответ. ![]()
Задача 11. Лёгкая пружина жёсткостью k и длиной l стоит вертикально на столе. С высоты H над столом на неё падает небольшой шарик массой m. Какую максимальную скорость будет иметь шарик при своём движении вниз, сжимая пружину? Трением пренебречь.
Ответ. ![]()
Задача 12. (МФТИ, 1971.) Самолёт
садится на палубу авианосца, имея скорость ![]() = 108 км/ч. Зацепившись
за канат торможения, он пробегает путь s = 30 м
до полной остановки. Определите максимальный вес
пилота при посадке, считая, что коэффициент
упругости каната не изменяется по мере его
растяжения. Масcа пилота m = 70 кг.
= 108 км/ч. Зацепившись
за канат торможения, он пробегает путь s = 30 м
до полной остановки. Определите максимальный вес
пилота при посадке, считая, что коэффициент
упругости каната не изменяется по мере его
растяжения. Масcа пилота m = 70 кг.
Ответ. 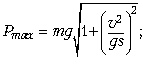 Pmax = 2200 Н.
Pmax = 2200 Н.
Задача 13. (МФТИ, 1974.) Два тела массами m и 3m движутся по взаимно перпендикулярным направлениям. После соударения тело массой m остановилось. Какую часть его энергии составляет выделившееся при ударе тепло?
Ответ. 2/3.