Пусть нам надо решить достаточно сложную задачу по динамике. И, хотя вряд ли можно указать конкретный путь к ответу в виде определённой последовательности шагов, в любом случае имеет смысл классифицировать такие задачи. Опыт показывает, что наиболее удачна классификация на основе характера ускорения тела. Другие классификации, например, по форме траектории, по физическим законам, по фигурирующим в задаче телам (блоки, наклонная плоскость и т.д.) менее эффективны.
Выбранная нами классификация представлена в таблице. Она, конечно, не всеобъемлющая, ведь мир физических задач весьма разнообразен, а исключения немногочисленны. Однако даже трудную задачу после отнесения к определённому типу проще решить.
Начнём с задач первого типа, для решения которых достаточно применения законов Ньютона. Отметим лишь, что совершенно не возбраняется применить вместо них закон сохранения энергии, упрощающий решение и делающий его физически красивым. Но изредка бывает, что закон сохранения энергии вырождается в тождество. Тогда его применить невозможно. Так, кстати, и случилось бы в следующей задаче.
Задача 1 (МФТИ, 1988). Космонавты,
высадившись на поверхности Марса, измерили
период вращения конического маятника, и он
оказался равным T = 3 с. Длина нити l =
1 м. Угол, составленный нитью с вертикалью, 
= 30°. Найдите
ускорение свободного падения на Марсе.
Решение.
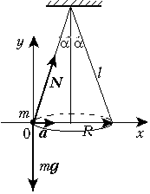
По второму закону Ньютона, ma = mg + N, где N – сила натяжения нити. В проекциях на оси X и Y векторное уравнение преобразуется в систему скалярных:
откуда a = gtg. Так как ускорение маятника 
где 
– радиус траектории
вращения маятника, то из уравнения 
легко находим марсианское
ускорение:
g = 3,8 м/с2.
Задача 2 (физфак МГУ им.
М.В.Ломоносова, 1996). По наклонной плоскости,
образующей угол
с горизонтом, втягивают за верёвку ящик массой M.
Коэффициент трения ящика о плоскость 
. Под каким углом к
плоскости следует тянуть верёвку, чтобы двигать
ящик равномерно с минимальным усилием?
Решение.
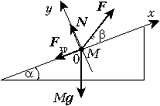
Векторное уравнение второго закона Ньютона:
Mg + F + N + Fтр = 0,
где Fтр – сила
трения скольжения (|Fтр| = |N|), N
– нормальная составляющая силы реакции
плоскости. Проецируем это уравнение на оси
координат X и Y:
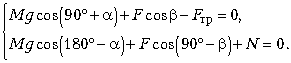
Последняя система уравнений легко приводится к виду:
откуда сразу следует:
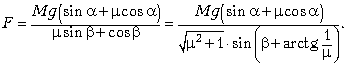
Очевидно, что минимальное значение
силы F будет при максимальном значении
знаменателя (числитель дроби постоянен), т.е. при 
Отсюда 
Переходим к задачам второго типа. Для их решения составляем динамико-энергетическую систему уравнений. Одно уравнение – по второму закону Ньютона, второе – по закону сохранения энергии. Уравнение второго закона Ньютона записываем в проекциях только на нормаль к траектории движения материальной точки. А вместо аналогичного проецирования на касательную, связанного с излишним применением высшей математики, применяем закон сохранения энергии. Это математически рационально.
Задача 3 (физфак МГУ им. М.В.Ломоносова, 1971). Малый тяжёлый шарик на нити вращается в вертикальной плоскости. Покажите, что шарик не сможет вращаться, если нить не в состоянии выдержать натяжение T, превышающее силу тяжести, действующую на шарик, в 6 раз.
Решение.
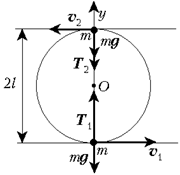
Рассмотрим два положения шарика – в самом низу и в самом верху. Составим для них уравнения по второму закону Ньютона:
ma1 = mg + T1; ma2 = mg + T2,
где T1 и T2 – соответствующие силы натяжения нити. Спроецируем эти уравнения на вертикальную ось Y:
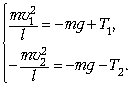
По закону сохранения энергии:
Окончательно получаем систему уравнений:
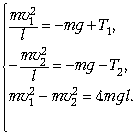
Теперь сложим первые два уравнения и сравним получившееся уравнение с третьим:
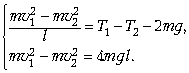
Сразу видим, что 
Поскольку 
что и требовалось доказать.
Заметим, что при неравномерном
движении по окружности вектор ускорения тела a
не направлен к её центру. Но проекция вектора a
на радиус окружности равна 
как и при равномерном движении.
Однако строгое доказательство этого факта
выходит за рамки школьной программы.
Задача 4 (физфак МГУ им. М.В.Ломоносова, 1979).
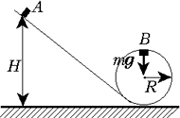
Небольшое тело соскальзывает по наклонной поверхности с высоты H = 1,2 м. Наклонная поверхность переходит в петлю. Найдите величину работы силы трения, если известно, что сила давления тела на петлю в верхней точке равна нулю, масса тела m = 10 г, радиус петли R = 0,4 м.
Решение. Работа A силы трения на
пути AB отрицательна и равна изменению
механической энергии тела: 
В точке B тело движется только под
действием силы тяжести, как это следует из
условия задачи. Поэтому 
откуда 
2 = Rg.
Следовательно:
A = mg(2,5 R – H); A = –2 • 10–2 Дж.
Окончание в № 12/07