В.Б.ДРОЗДОВ, г. Рязань

Движение заряда в магнитном поле

Задача 1. В однородное магнитное поле индукцией B влетает со скоростью частица массой m и зарядом q. Угол между вектором скорости и вектором магнитной индукции B равен . Определите, как будет двигаться частица в магнитном поле.

Решение.

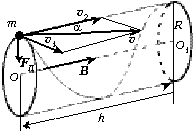
Рассмотрим случай  = 0. При этом сила Лоренца равна нулю и на заряд не действует. Следовательно, он будет двигаться прямолинейно с постоянной скоростью , т.е. по инерции. Легко видеть, что вариант произвольного угла представляет собой комбинацию двух частных случаев: ₁ = 90° и ₂ = 0.

Разложим вектор на две составляющие и . Интуитивно ясно, что частица будет совершать вращательное движение по поверхности цилиндра, равномерно перемещаясь со скоростью ₂ вдоль его образующей.

Радиус цилиндра R определяется из уравнения (сила Лоренца действует на тело только благодаря составляющей скорости ₁):

Период обращения частицы . Он не зависит ни от модуля скорости , ни от её направления, определяемого углом .

Траектория заряда – винтовая линия, «навитая» на цилиндр. Её шаг – расстояние, проходимое вдоль образующей за один оборот:

Приведённое решение не вполне строгое, но вполне приемлемое, ибо большего сделать сейчас нельзя. А строгое решение основывается на интегрировании дифференциального уравнения Его проведёт абитуриент, когда станет студентом.

Задача 2 (МФТИ, 1978; физфак МГУ им. М.В.Ломоносова, 1981).

Электрон влетает в однородное магнитное поле индукцией B. В точке A он имеет скорость , которая составляет с направлением поля угол . При каких значениях индукции магнитного поля электрон окажется в точке D? Расстояние АD = L.

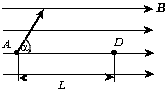
Решение. Очевидно, что на расстоянии L должно уложиться целое число шагов винтовой линии, т.е.

Отсюда получаем неоднозначный ответ:

где n = 1, 2, 3, ...

Решение краткое, однако на экзамене придётся вывести формулу шага винта (см. задачу 1).

Задача 3. Однородные магнитное и электрическое поля перпендикулярны друг другу. Напряжённость электрического поля E, индукция магнитного поля B. С какой скоростью и в каком направлении должен лететь протон, чтобы двигаться прямолинейно?

Решение. Интуитивно подобранная векторная конфигурация полей и сил изображена на рисунке.

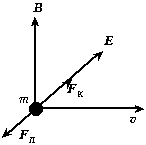
Скорость протона перпендикулярна обоим векторам – E и B. Очевидно, что движение частицы может быть прямолинейным в том и только в том случае, когда сила Лоренца F_Л и кулоновская сила F_К компенсируются: F_Л + F_К = 0. Отсюда следует равенство модулей: F_Л = F_К, значит, qB = qE и При этом прямолинейное движение протона будет ещё и равномерным. Легко видеть, что при любой другой скорости (как по модулю, так и по направлению) движение частицы будет криволинейным и неравномерным.

Задача 5 (физфак МГУ им. М.В.Ломоносова, 1990). Электрон движется в однородных и постоянных электрическом и магнитном полях, направленных по оси Z. В начальный момент электрон пересекает начало координат, двигаясь в направлении оси X. В каких точках электрон вновь пересечёт ось Z? Напряжённость электрического поля E, индукция магнитного поля B, заряд электрона e, масса электрона m.

Решение. На рисунке изображены направления полей и сил, действующих на электрон. Он будет двигаться как бы по винтовой линии со всё увеличивающимся шагом (конечно, строго это не винтовая линия).

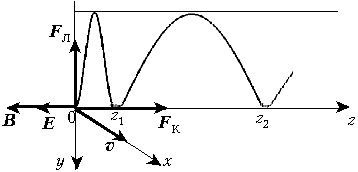
Ведь по оси Z на электрон действует кулоновская сила. Координата точки пересечения частицы с осью Z после n витков , где – проекция ускорения электрона на ось Z, – его период обращения в плоскости XOY. Отсюда: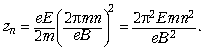

Задача 5. Протон движется в однородном магнитном поле по винтовой линии радиусом R и шагом h. Индукция магнитного поля B. Найдите скорость частицы.

Решение. Из результата задачи 2 вытекает система уравнений:

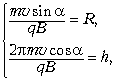
где m и q – масса и заряд протона соответственно.

Запишем равносильную систему:

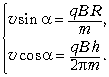
Возведём обе части уравнений в квадрат и скложим, учитывая, что:

Легко определим и угол (скорость ведь вектор!):

Задача 6 (мехмат МГУ им. М.В.Ломоносова, 1983). Электрон движется в однородном магнитном поле индукцией B. В начальный момент времени он находился в точке O, и его скорость была перпендикулярна вектору магнитной индукции. Найдите расстояние l от электрона до точки O в момент времени t. Массу электрона m и его заряд q считать известными.

Решение.

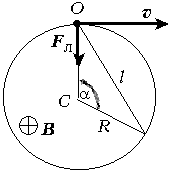
Из рисунка геометрически ясно, что где – угол поворота радиус-вектора электрона, – его угловая скорость. Поскольку и

Задача 7. -частица влетает по нормали в область поперечного однородного магнитного поля индукцией B = 0,1 Тл. Область магнитного поля заключена между параллельными плоскостями, расстояние между которыми равно h = 0,1 м. Найдите скорость частицы, если после прохождения магнитного поля она отклонится на угол  = 30° от первоначального направления. Для -частицы отношение заряда к массе (удельный заряд)

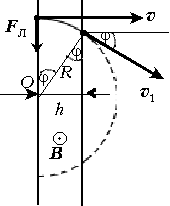
Решение. Здесь мы имеем дело с локализованным в пространстве магнитным полем. Поэтому траекторией -частицы будет не вся окружность, а её дуга. Из уравнения находим где R – радиус дуги. Поскольку

Числовой расчёт даёт:  = 106 м/с.

Продолжение в № 10