Продолжение. См. № 17, 19/06 Варианты вступительных экзаменов по физике-2005 7–11-й классы (Печатается по сб.: В.П.Демков, В.В.Озолин, Е.Л.Студников. Варианты вступительных экзаменов в МАИ в 2005 г. по физике: Учебное пособие. – М.: ООО «Эрфольг-А», 2005.) Вариант № 4 1. Две детали скрепляют болтом и гайкой. При закручивании гайки болт не удерживают, в результате чего он прокручивается, причём за один оборот гайки болт поворачивается на четверть оборота. Сколько оборотов нужно сделать гайкой, чтобы скрепить детали, если для этого гайка должна пройти N = 15 витков резьбы болта? Дано: N = 15. ______________ N' – ? Решение Угловые скорости гайки и болта равны: 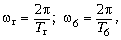где Tг – время одного оборота гайки; Tб = 4Tг – время одного оборота болта. 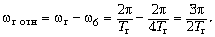В системе отсчёта, связанной с болтом, угловая скорость гайки В системе отсчёта, связанной с болтом, совершив N витков, гайка пройдёт угол 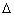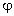= 2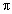N и будет полностью завёрнута. Запишем уравнение движения гайки по окружности в виде 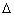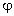= 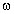г отн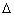t, где 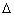t – время закручивания гайки. 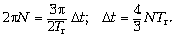Следовательно, Поскольку время закручивания гайки во всех системах отсчёта одинаково, то 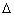t = N ' Tг, где N' – число оборотов гайки в системе «земля». Следовательно, 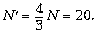2. Для садовых дорожек завезли полную машину гравия. Масса гравия m = 5 т, объём кузова машины V = 3,3 м3. Определите среднюю плотность гравия. Дано: m = 5 т, V = 3,3 м3. ________________ 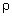– ? 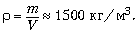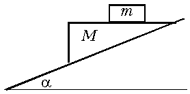Решение Плотность вещества связана с его массой и объёмом соотношением 3. С наклонной плоскости с углом при основании 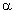 = 30° соскальзывает без трения клин массой M = 1 кг, верхняя грань которого горизонтальна. На клине находится брусок массой m = 2 кг. Коэффициент трения между бруском и клином 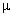 = 0,6. Найдите силу трения, действующую на брусок. Дано: 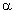 = 30°, M = 1 кг, m = 2 кг, 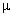= 0,6. _____________ Fтр – ? Решение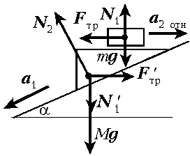 На брусок действуют сила тяжести mg, сила реакции N1 со стороны клина и сила трения Fтр. На клин действуют сила тяжести Mg, сила давления N'1 cо стороны бруска, сила реакции N2 наклонной плоскости и сила трения Fтр' между поверхностями бруска и клина, причём N1' = – N1, Fтр' = – Fтр. Под действием этих сил клин будет двигаться вниз вдоль наклонной плоскости с ускорением a1, а брусок будет либо двигаться вместе с клином с ускорением a1 (т.е. покоиться на поверхности клина), либо двигаться с ускорением a2. Рассмотрим случай, когда брусок движется относительно клина. При этом ускорение a2 бруска можно представить в виде a2 = a1 + a2 отн, где a2 отн – ускорение бруска относительно клина, направленное горизонтально и вправо. Запишем уравнения движения клина и бруска: m(a1cos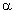 – a2 отн) = Fтр; –ma1sin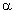 = N1 – mg; Fтр = 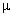N1; Ma1 = Mgsin 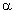+ N1sin 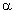– Fтрcos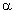. Следовательно: N1 = mg – ma1sin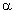; m(a1cos 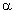– a2 отн) = 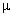(mg – ma1sin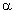); Ma1 = Mgsin 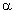+ (mg – ma1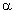sin)(sin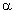 – 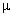cos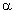). 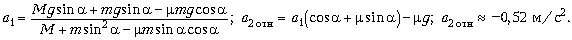Отсюда находим: Этот результат означает, что ускорение бруска относительно клина направлено по горизонтали влево, что исключено условием задачи. Следовательно, a2 отн = 0, т.е. брусок покоится на клине. Запишем уравнение движения клина с бруском в виде (M + m) a1 = (M + m)gsin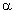. Отсюда находим a1 = gsin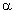. Из уравнения движения бруска ma1cosa = Fтр получаем ответ: Fтр = mgsin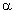•cos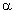 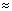 8,5 Н. 4. Груз начинают поднимать из состояния покоя вертикально вверх с постоянным ускорением. Во сколько раз работа, совершённая за вторую секунду движения, меньше работы, совершённой за третью секунду движения? Дано: 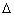t2 = 1 c, 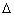t3 = 1 c. ______________ A3/A2 – ? Решение Пусть груз поднимают вертикально вверх с ускорением a под действием постоянной силы F. Работа, совершённая силой F за вторую секунду движения груза, A2 = F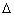s2, где 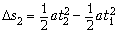– путь, пройденный грузом за вторую секунду (t1 = 1 c, t2 = 2 c). Аналогично: работа, совершённая силой F за третью секунду движения груза, A3 = F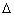s3, где 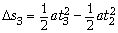– путь, пройденный грузом за третью секунду (t2 = 2 c, t3 = 3 c). Следовательно, 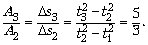5. Найдите скорость распространения звука в материале, в котором колебания периодом T = 0,01 с вызывают звуковую волну, имеющую длину волны 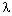 = 10 м. Дано: T = 0,01 с, 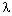 = 10 м. _____________ 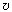– ? Решение Длина волны равна расстоянию вдоль направления её распространения между двумя соседними максимумами (или минимумами) в волне, т.е. расстоянию, которое проходит, например, максимум волны за один период колебаний: 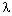 = 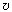T. Следовательно, 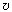= 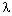/T = 103 м/с. 6. Парциальное давление паров ртути в воздухе при температуре t = 20 °С равно p = 0,133 Па. Сколько атомов ртути содержится в объёме V = 1 м3 воздуха? Дано: t = 20 °С, p = 0,133 Па, V = 1 м3. _______________ N – ? Решение Из уравнения состояния идеального газа p = nkT, найдём концентрацию атомов паров ртути в воздухе: n = p/kT. Следовательно, число атомов ртути в указанном объёме N = nV = 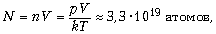где (T = t + 273) К.

.  .