Продолжение. См. № 1/06 К.Ю.БОГДАНОВ, школа № 1326, г. Москва KBogdanov@mtu-net.ru Синтез наук – оружие познания XXI века Элективный курс, 10–11-й классы, естественнонаучный профиль (136 ч, 2 ч/нед.) Уроки 43–44 (11-й класс). Теория плавания с ластами, Рейнольдсом, штопором, кавитацией и без... Если спросить у любого, как он плавает, то следует, по-видимому, ожидать два варианта ответа. В первом случае вам начнут объяснять, каким стилем и как быстро они преодолевают водные преграды. Во втором – скажут, что садятся в лодку, катер или на корабль. Вряд ли найдётся человек, который станет объяснять физические основы нашей способности держаться на воде или вычислять коэффициент полезного действия гребцов в лодке. Попробуем сыграть роль такого человека – теоретика плавания – и ответить на несколько вопросов, касающихся физической теории плавания. Почему мы сразу не тонем? Хорошо умеющих плавать обидит такая форма вопроса. Однако твёрдо установлено, что человек, оставшийся один на один с водной стихией далеко от берега, рано или поздно всё равно утонет. Объясняют это тем, что у несчастного кончаются силы, и он перестаёт совершать плавательные движения, за счёт которых он держится на поверхности воды. Как это ни обидно, но даже самые умные из нас примерно на 70% состоят из обычной воды. Поэтому бытующее в народе мнение, что если человека сильно ударить, то от него «одно мокрое место» останется, имеет под собой вполне научную основу. Таблица показывает, из чего мы состоим на самом деле и какова плотность этих компонент. 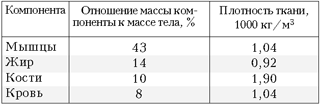Большую часть нашего тела составляют мышцы. Так как их плотность больше, чем у воды, то при плавании они должны тянуть нас на дно. Ещё больше, как следует из таблицы, нас тянут на дно наши кости. Кажется, что только жировая прослойка может спасти нас от быстрой гибели. Однако это не совсем верно. Внутри каждого человека есть воздушный мешок – лёгкие. Объём воздуха в лёгких человека может изменяться от 1 л (при глубоком выдохе) до 6 л (при глубоком вдохе). Так как плотность воздуха приблизительно в 800 раз меньше, чем у воды, то каждый литр воздуха в наших лёгких по закону Архимеда создаёт подъёмную силу около 9,8 Н. Соответственно, плотность тела человека 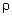ч изменяется от 940–990 кг/м3 при полном вдохе до 1010–1070 кг/м3 при полном выдохе. Голова – всему помеха! Оценивая плавучесть человека, необходимо учитывать, что голова, объём которой составляет около 7% объёма его тела, всегда должна находиться над поверхностью воды. Пусть человек в воде занимает вертикальное положение. Легко показать, что в таком случае справедлива следующая формула для отношения абсолютных величин архимедовой силы FA и силы тяжести Fg, действующих на человека в воде: 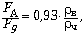             (1) где 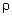в – плотность воды. Из (1) следует, что даже при самом глубоком вдохе архимедовой силы не хватит для полной компенсации силы тяжести плывущего человека. Но даже если архимедова сила была бы равна силе тяжести, человек не смог бы неподвижно лежать в воде, находясь в горизонтальном положении. Это вызвано тем, что архимедова сила и сила тяжести приложены к разным точкам тела. FA приложена в центре масс вытесненной телом жидкости (т. А на рисунке), а Fg – в центре масс тела, чуть ниже пупка (т. G), в точке, которая из-за наличия воздуха в лёгких находится всегда дальше от головы, чем т. А. В результате FA и Fg образуют пару сил, которая вращает тело в вертикальной плоскости, пока оно не примет вертикальное положение. 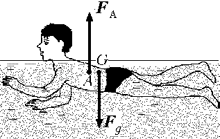Поворот тела из горизонтального положения в вертикальное под действием пары сил: силы тяжести Fg и выталкивающей FA Легко ли плыть в вертикальном положении? Итак, если считать, что в вас достаточно жира и воздуха, чтобы сразу не утонуть, то можно утверждать, что вскоре после того, как вас бросят в воду, вы примете вертикальное положение. Однако каждому ясно, что плыть вперёд, находясь в вертикальном положении, очень трудно – мешает огромное сопротивление жидкости, которое, как известно, пропорционально площади поперечного сечения двигающегося тела. Интересно, что одним из требований, предъявлявшихся к пловцам первого разряда на флоте царской России, было умение проплыть стоя, без помощи рук, 20 саженей (1 морская сажень = 1,83 м). Оценка показывает, что площадь поперечного сечения тела человека на уровне пояса почти в 10 раз меньше, чем аналогичная вдоль позвоночника. Поэтому перед тем, как плыть, лучше всё-таки принять горизонтальное положение. Обычно это делают просто – болтая ногами. Что мешает болтать ногами? Найдём силу сопротивления F, действующую на тело при его движении в воде со скоростью 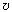. Силы сопротивления жидкости или газа зависят от скорости движения тел. При малых 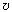почти все частицы перед движущимся на них телом имеют достаточно времени, чтобы отойти в сторону, не приобретая при этом импульса в направлении скорости, и только те частицы, которые коснулись тела, обретают его скорость. Эти сдвинутые с места частицы, двигаясь вместе с телом, будут в свою очередь увлекать очень тонкий слой жидкости, с которым они тесно связаны. Чем крепче связаны между собой частицы жидкости или, что то же самое, чем больше её вязкость, тем больше сила сопротивления, действующая на тело. В этом случае сила сопротивления прямо пропорциональна величине скорости |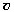|, среднему размеру тела в плоскости, перпендикулярной 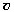, и вязкости жидкости. Точную формулу для силы сопротивления при малых 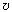можно получить, например, для тела, имеющего форму шара. Эта формула, получившая название формулы Стокса, имеет вид: 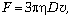             (2) где 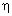– коэффициент вязкости, равный для воды 0,001 Па . с, D – диаметр шара. Таким образом, если скорость движения тела невелика, то на него будет действовать сила, прямо пропорциональная величине скорости и обратная ей по направлению. Пусть теперь скорость тела возросла, и все частицы жидкости, находящиеся на его пути, уже не успевают отходить в сторону и увлекаются вперёд. В этом случае за t секунд тело успеет натолкнуться на массу жидкости, равную 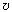tS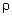в, где S – площадь поперечного сечения тела в направлении, перпендикулярном 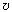. Всей этой массе жидкости тело сообщит скорость 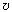и импульс 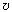2tS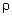в. 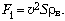Поэтому силу сопротивления F1, действующую на тело со стороны жидкости при больших скоростях (её часто называют силой лобового сопротивления), можно вычислить по следующей формуле:              (3) Конечно, и при больших скоростях некоторая часть силы сопротивления зависит от вязкости и может быть оценена по выражению (2). Чтобы оценить, как изменяется вклад «вязких» сил сопротивления с увеличением скорости тела, найдём отношение F1 к F для шара диаметром D, используя формулы (2) и (3): 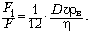             (4) Выражение 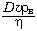, являющееся безразмерной величиной, называется числом Рейнольдса Re. Из (4) следует, что при Re > 100 вязкостью среды можно пренебречь, а силу её сопротивления вычислять по формуле (3). Наоборот, при малых числах Рейнольдса (Re < 1) следует учитывать вязкость жидкости и пользоваться формулой (2). Русалка с ластом и число Рейнольдса. После такого отступления в область гидродинамики вернёмся к задаче о том, как нужно болтать ногами, чтобы перевести наше тело из вертикального положения в горизонтальное. Чтобы упростить задачу, будем считать, что мы используем для этого один ласт, надетый на обе ноги (превратимся в русалку). Тело русалки заменим полузатопленным поленом, к нижнему концу его прикрепим подвижный ласт, имеющий поверхность площадью S, который может двигаться в горизонтальном направлении. Будем также считать, что ласт не деформируется при движении, а его масса пренебрежимо мала по сравнению с массой полена, чтобы не учитывать перемещений суммарного центра масс при изменении положения ласта относительно полена. 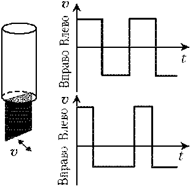Модель русалки, пытающейся перейти из вертикального положения в горизонтальное, двигая ластом. На графиках показаны изменения скорости ласта v от времени при симметричном (вверху) и несимметричном (внизу) движениях Пусть частота болтания ластом составляет 1 Гц, а амплитуда движений 0,25 м. Тогда средняя скорость его движения 0,5 м/с. Считая, что «размер» ласта около 0,2 м2, а вязкость воды 0,001 Па . с, получаем Re = 100 000. Таким образом, при болтании ногами «вязкими» силами можно пренебречь и силу сопротивления вычислять по формуле (3). Симметрично или нет? Пусть сначала график изменения скорости ласта от времени выглядит симметрично, т.е. скорость и интервалы движения им влево и вправо одинаковы. Очевидно, что в этом случае и сила сопротивления воды, а также её средний импульс при движении влево и вправо тоже будут одинаковы, а значит, тело русалки так и останется вертикальным. Попробуем теперь двигать ласт влево с большей скоростью (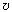1), чем вправо (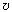2). Так как расстояния, проходимые ластом при его движениях влево и вправо, должны быть равны, то 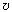1t1 = 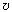2t2, где t1 и t2 – соответствующие длительности движения. Легко показать, что при таких «несимметричных» движениях средняя сила Fср, действующая на русалку и направленная вправо, равна 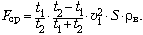             (5) Таким образом, любые повторяющиеся несимметричные движения ластами приведут к тому, что мы примем горизонтальное положение и поплывём. А если бы мы оказались в бочке с мёдом? Вязкость мёда в 10 000 раз больше, чем у воды. Поэтому двигать ластами, находясь в бочке с мёдом, очень трудно. Даже если предположить, что скорость наших движений в таких условиях уменьшится только в 10 раз (с 0,5 м/с до 0,05 м/с), то отношение силы лобового сопротивления к вязкой силе, вычисленное по формуле (4), составит менее 1/10. Это значит, что основными силами, действующими при движении ласта в мёде, являются силы вязкости. Попробуем теперь получить выражение для Fср, аналогичное (5), используя формулу (2) для несимметричных движений. Как легко показать, при любых 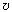1 , t1 и 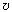2 , t2 , для которых справедливо равенство 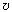1t1 = 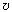2t2, средняя за цикл сила, действующая на ласт, будет равна нулю. А это значит, что в очень вязкой жидкости, где число Re 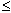1, плавать надо не так, как в воде, а по-другому. Большие трудности малых существ. Как следует из формулы (4), очень малые существа, даже плавая в воде, могут сталкиваться с такими же трудностями, что и мы в воображаемом медовом озере. Известно, что бактерии, размер которых около 1 мкм, плавают в воде со скоростью 0,1 мм/с. Легко посчитать число Рейнольдса для таких движений – оно близко к 10–4, что заставляет эти существа использовать при плавании только силы вязкого трения. Как же двигают бактерии своими жгутиками, чтобы продвинуться? Диаметр жгутика чуть больше 100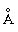 (1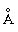 = 10–10 м) и, конечно, лишён мускулатуры. Поэтому бактерия не может по своему желанию согнуть жгутик или пустить вдоль него волну деформации, как делают змеи или некоторые рыбы для своего движения. Единственное, что может делать бактерия, – закручивать жгутик вдоль оси, как штопор. Для этого в месте соединения жгутика с телом бактерии есть специальный молекулярный моторчик – предмет исследований учёных, которые до сих пор до конца не знают, как он работает. Бактерии вращают жгутиком с частотой несколько герц, часто меняя направление движения. 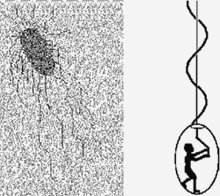Фото бактерии кишечной палочки (слева, стрелкой указан один из жгутиков) и схематическое изображение (справа) принципа её движения – вращение жгутиком как штопором Все знают, что круговые движения штопора продвигают его либо вперёд, либо назад, в зависимости от того, против или по часовой стрелке мы его крутим. То же самое происходит и с бактерией: жгутик «вкручивается» или «выкручивается» из жидкости, которая для него является очень вязкой (Re < 10–5), продвигая бактерию вперёд или назад. Как плыть быстрее? Для этого необходимо не только изо всех сил двигать руками и ногами в определённой последовательности, но и ориентировать своё тело так, чтобы испытывать минимальное сопротивление воды. Согласно формуле (3), сила сопротивления воды пропорциональна площади поперечного сечения S, однако это выражение даёт завышенное значение для F1, т.к. не все частицы воды при столкновении с телом приобретают его скорость. Однако формулой (3) можно пользоваться, если выражение в её правой части умножить на безразмерный коэффициент CD – коэффициент лобового сопротивления: 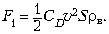(6) Как показывают эксперименты, CD сильно зависит от формы тела, как это показано на рисунке. 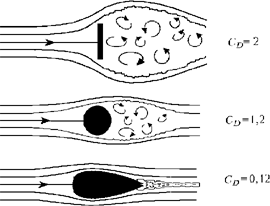Линии тока жидкости при обтекании диска (вверху), шара (в середине) и каплевидного тела (внизу) одной и той же площади поперечного сечения. Справа приведены соответствующие значения для CD при Re = 100 000 Большие различия в CD возникают из-за того, что вода по-разному обтекает эти тела. За диском и шаром, например, образуется зона вихрей. А это значит, что, двигая их вперёд, мы должны тратить энергию не только на преодоление вязкого трения, но и на образование вихрей. В отличие от шара и диска, за каплевидным обтекаемым телом вихри почти не образуются, и поэтому сила сопротивления воды движению такого тела меньше, хотя площадь его поперечного сечения такая же. Как плавают рыбы? Число Рейнольдса для небольших рыб более 100, поэтому вращать «штопор», как это делают бактерии, им невыгодно. Рыбы используют, по крайней мере, два способа плавания – волнообразно извиваясь всем телом или двигая только хвостом. Рыбы, имеющие змееобразную форму (например, угорь), плавают первым способом, так что изгиб тела движется от головы к хвосту, отталкивая назад воду, в результате чего рыба движется вперёд. При втором способе воду отталкивает назад только быстро распрямляющийся хвост рыбы. 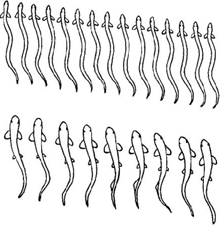Два способа плавания рыб – с помощью волнообразного движения всего туловища (вверху) и только хвоста (внизу) Неразгаданные загадки плавания меч-рыбы и дельфина. Учёные до сих пор не могут ответить на вопрос, как многие рыбы и дельфины умудряются двигаться в воде со скоростями, недоступными иногда даже для птиц в воздухе. Меч-рыба, например, плывет со скоростью до 130 км/ч; тунец – 90 км/ч. Если изготовить муляж меч-рыбы и подсчитать коэффициент лобового сопротивления CD, то окажется, что рыбе необходимо развить мощность автомобильного мотора – около 100 л.с. Энергия живых существ – это энергия окислительных процессов. Но рыбы – существа холоднокровные, их температура ненамного выше температуры воды, в которой кислород, кстати, растворён в очень небольшом количестве. Поэтому такие мощности для них просто недостижимы! Остаётся предположить, что рыбы каким-то образом «умеют» очень сильно снижать сопротивление воды. Меч-рыба При быстром движении обычного предмета через воду вихри образуются только позади тела. Согласно закону Бернулли, давление в них падает, что оказывает на тело тормозящее действие. Одна из гипотез, объясняющих резкое снижение сопротивления воды движению меч-рыбы, состоит в том, что меч, находящийся впереди, служит генератором вихрей, которые переходят на тело рыбы. В результате рыба движется, будучи со всех сторон окружена вихрями – областями низкого давления, что соответствует чрезвычайно низкому сопротивлению движению. Такого же эффекта можно достичь, если поверхность тела сделать шероховатой, возмущая пограничный слой между телом и жидкостью и превращая её течение в вихревое (турбулентное) по всей поверхности контакта. Какой из этих механизмов уменьшения СD реализуется у меч-рыбы учёные до сих пор не знают. Почему щука всегда догонит карася? Общеизвестна поговорка «На то и щука в море, чтобы карась не дремал». Каждому ясно, что щука всегда догонит карася, если он, конечно, не успеет где-нибудь спрятаться. Да и не только карася, а любую мелкую рыбёшку. Но почему максимальная скорость у крупной рыбы больше, чем у мелкой? Согласно (6), сила сопротивления, которую преодолевает рыба, двигаясь в воде, при одинаковой форме тела пропорциональна площади его поперечного cечения и квадрату скорости. Поэтому выражение для мощности, которую затрачивает рыба при движении, имеет вид: N = k1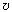3,                  (7) где k1 = 0,5CDS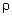в. Оценим, как связана максимальная мощность, развиваемая мышцей животного, с её размерами. Известно, что максимальная сила каждой мышцы пропорциональна площади её поперечного сечения, а именно, каждый квадратный сантиметр мышцы способен развить силу около 50 Н. Мышца, развивая силу, укорачивается пропорционально исходной длине, максимально – на 50%. Значит, максимальная работа, производимая каждой мышцей и равная произведению максимальной силы на максимальное укорочение, должна быть пропорциональна её объёму. Так как механизм сокращения всех мышц одинаков, то и максимальная мощность также должна быть пропорциональная объёму мышцы. Если считать, что большие и маленькие рыбы подобны, используют один и тот же стиль плавания и аналогичные мышцы, то их максимальная мощность должна быть прямо пропорциональна объёму мышц, занятых в движении. А так как рыб мы считаем подобными, то максимальная мощность рыбы должна быть прямо пропорциональна её объёму: N = k2V,              (8) где V – объём рыбы, а k2 – постоянный коэффициент, зависящий от её типа и стиля плавания. Приравнивая (7) и (8), получаем 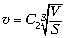,                          (9) где C2 – коэффициент, не зависящий от размеров рыбы. Пусть 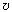1, 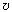2, V1, V2, S1, S2 – скорости, объёмы и площади поперечного сечения большой и маленькой рыб соответственно. Тогда из (9) получаем: 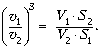             (10) Считая формы большой и маленькой рыб подобными, а их длины равными L1 и L2 , можно утверждать, что V1/V2 = (L1/L2)3 , а S1/S2 = (L1/L2)2. 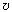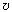Поэтому выражение (10) можно переписать в виде (1/2)3 = L1/L2. Если учесть, что длина тела щуки около 1 м, а карася 0,1 м, то перспектива карасю попасть в пасть щуки вырисовывается вполне чётко. Рост известных пловцов тоже выше среднего, как и у баскетболистов. Например, рост многократного олимпийского чемпиона по плаванию Александра Попова 197 см. Очевидно, успехи «гулливеров» в плавании можно объяснить так же, как и историю со щукой и карасём. Почему мелкая рыба ходит косяками? В косяке все рыбы движутся в одном направлении друг за другом. При этом количество рыб в косяке может быть от нескольких штук до миллионов. Плыть в косяке не только безопаснее, но и энергетически выгоднее, если держаться точно за виляющим впереди хвостом, который оставляет после себя завихрения, подталкивающие вперёд тех, кто плывёт сзади. Двигаться так, чтобы оказаться точно между двумя завихрениями, оставленными впереди плывущей рыбой, помогают специальные рецепторы боковой линии – высокочувствительные датчики давления. Косяк мелкой рыбы и кольца завихрений в нём, облегчающие рыбам движение вперёд Что мешает двигаться в воде со скоростью звука? Вся энергия при движении в воде уходит на преодоление силы её сопротивления. Вязкость воды в 50 раз, а плотность в 800 раз больше, чем у воздуха. Это и является основной причиной того, что самолёты летают в десятки, а иногда и сотни раз быстрее, чем плывут обычные подводные лодки и торпеды (не более 130 км/ч). Тормозят движение в воде не только большие вязкость и плотность, но и зоны низкого давления (турбулентности и вихри), возникающие на хвосте подлодок и торпед. В тех местах вокруг, где давление падает ниже давления насыщенных паров воды (0,023 атм при нормальных условиях), образуются пузырьки пара. Такой пузырёк пара называют кавитационным пузырьком, а процесс – кавитацией. Последующее схлопывание кавитационных пузырьков порождает ударные волны, которые являются причиной акустического шума подводных лодок и вызывают эрозию их гребных винтов. Поэтому раньше, когда конструировали обычные торпеды и подводные лодки, всегда боролись с возникновением кавитационных пузырьков пара. Что нам мешает, то и поможет! Ещё в начале 1960-х гг. перед советскими учёными была поставлена задача – разработать принцип движения под водой со скоростями, близкими к скорости звука. И тогда возникла идея превратить заклятого врага, кавитацию, в помощника. Если не бороться с кавитацией, а, наоборот, создать все условия для неё, то движущееся под водой тело будет со всех сторон окружено облаком кавитационных пузырьков. Такие условия, названные суперкавитацией, приводят к тому, что тело перестаёт соприкасаться с водой и как будто летит в окружающем её газовом пузыре, а значит, резко уменьшается сила сопротивления и соответственно увеличивается скорость движения под водой. Очевидно, что сила тяги гребного винта в условиях суперкавитации падает, т.к. со всех сторон он окружён газовыми пузырьками. Поэтому в качестве источника тяги в таких условиях больше подходит ракетный двигатель. В 1977 г. противолодочная торпеда «Шквал», движущаяся в условиях суперкавитации со скоростью более 100 м/с, была принята на вооружение ВМФ СССР. Секрет технологии таких подводных средств не могли раскрыть в течение 30 лет, и только в середине 2005 г. Германия заявила, что разработала аналогичную высокоскоростную торпеду «Барракуда». В настоящее время учёные и конструкторы пытаются использовать суперкавитацию для создания пассажирских подводных судов. Торпеда «Шквал», летящая в суперкавитационном пузыре ОТ РЕДАКЦИИ. См. также статью Ашли С. «Необычное движение под водой» в «Физике № 29/02, а также сайт http://shipandship.chat.ru/neptun – картинка модели дельфиньей кожи. Продолжение в № 11

.  .