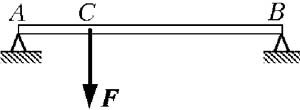
5 Невесомый стержень лежит горизонтально на двух опорах A и B. В точке C к стержню приложена сила F, направленная вертикально вниз. Определите величину этой силы, если известно, что расстояние CB в k = 2,5 раза превышает расстояние AC, а нагрузка на опору A превышает нагрузку на опору B на величину f = 30 Н.
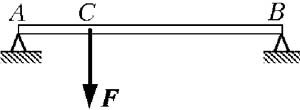
Решение
Пусть l – длина стержня. Обозначим через x расстояние AC, а через FA и FB – силы реакции опор, действующие на стержень в точках A и B. Условия равновесия стержня имеют вид:
FA + FB = F; FAx = FB(l – x).
Кроме того, по условию задачи,
FA – FB = f, 
Решая эту систему уравнений, получаем ответ:
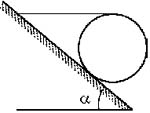
6 Сплошной
однородный цилиндр массой m располагается на
шероховатой наклонной плоскости, образующей с
горизонталью угол 
. На цилиндр намотана нить, которая
закреплена на наклонной плоскости так, что её
отрезок между цилиндром и точкой закрепления
горизонтален. Найдите силу F, с которой цилиндр
действует на плоскость, если известно, что он
находится в равновесии. Ускорение свободного
падения g.
Решение
Цилиндр находится в равновесии под
действием сил, изображённых на рисунке, где mg –
сила тяжести, T – сила натяжения нити, F' – сила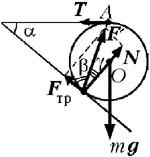
реакции наклонной плоскости. Последнюю удобно
разложить на две составляющие: силу нормального
давления N и силу трения Fтр. Поскольку линии
действия сил mg и T пересекаются в точке A, линия
действия силы F' при равновесии цилиндра также
должна проходить через эту точку. Следовательно,
Записывая уравнение моментов относительно оси, проходящей через точку O, находим, что N = mg.
Из рисунка видно, что 
Отсюда 
По третьему закону Ньютона, величина
искомой силы F = F'. Объединяя записанные
равенства, находим, что
7 Тонкую
деревянную палочку подвесили за один из концов
на нити, а другой конец опустили в воду. При этом
палочка оказалась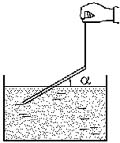 
наклонённой к горизонтали
под углом = 30°,
а длина её части, погружённой в воду, составила
половину длины палочки. Какую работу A нужно
совершить, чтобы вытащить за нить палочку из
воды? Длина палочки L, площадь сечения S, плотность
воды 
в, ускорение
свободного падения g.
Решение
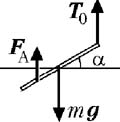Плавающая палочка находится в
равновесии под действием сил, изображённых на
рисунке, где mg – сила тяжести, FA –
архимедова сила, T0 – сила натяжения нити.
Из уравнения моментов, записанного относительно
оси, проходящей через точку подвеса палочки,
получаем
откуда плотность материала палочки 
а её масса 
Следовательно,
сила натяжения нити в исходном положении палочки
равна
Поскольку в уравнении моментов
зависимость от угла наклона палочки сохраняется,
глубина погружения палочки в воду при любом угле
наклона одна и
та же. Поэтому при перемещении нити вверх сила
натяжения будет оставаться постоянной до тех
пор, пока палочка не займёт вертикальное
положение, оставаясь погружённой в воду
наполовину. Совершённая при этом работа
При дальнейшем подъёме нити сила натяжения будет возрастать в зависимости от перемещения по линейному закону. Обозначив через x длину выступающей из воды части палочки, имеем
причём 
Среднее значение этой силы при удалении палочки из воды
Совершённая при этом работа
Полная работа A = A1 + A2. Тогда
8 Математический маятник длиной l = 0,5 м
подвешен на штативе, закреплённом на тележке,
которая скатывается с наклонной плоскости.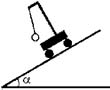
Найдите период T малых колебаний маятника
относительно тележки. Считать, что масса тележки
значительно больше массы маятника, а силы трения
пренебрежимо малы. Ускорение свободного падения
g = 9,8 м/с2. Угол наклона плоскости к
горизонту = 30°.
Решение
Рассмотрим колебания маятника в
поступательно движущейся системе отсчёта,
связанной с тележкой. Обозначив через g' величину
ускорения свободного падения в этой системе, по
формуле Гюйгенса находим, что период малых
колебаний математического маятника равен
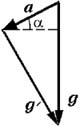
Согласно закону сложения векторов ускорений, ускорение точки в неподвижной системе равно векторной сумме ускорения точки в поступательно движущейся системе и ускорения движущейся системы. Обозначив через a ускорение тележки, получаем
g = g' + a.
Вектор a направлен вдоль наклонной
плоскости и равен по модулю a = gsin. Как видно из рисунка, g'2 =
(acos)2 + (g –
asin)2.
Отсюда g' = gcos.
Тогда
