1 Беговые
дорожки легкоатлетического стадиона состоят из
двух прямолинейных участков, соединённых двумя
полуокружностями. Ширина дорожки d = 1 м. Линия
старта проведена перпендикулярно
прямолинейному участку дорожек и совпадает с
линией финиша. Два бегуна, находящиеся на первой
(внутренней) и второй дорожках, одновременно
принимают старт и пробегают до финиша один круг.
Они разгоняются равноускоренно, пока не наберут
максимальную скорость ![]() 0 = 8 м/с, одинаковую для обоих
бегунов, с которой и пробегают оставшуюся часть
дистанции. На сколько отличаются времена разгона
бегунов, если, двигаясь каждый по середине своей
дорожки, они финишируют одновременно?
0 = 8 м/с, одинаковую для обоих
бегунов, с которой и пробегают оставшуюся часть
дистанции. На сколько отличаются времена разгона
бегунов, если, двигаясь каждый по середине своей
дорожки, они финишируют одновременно?
Решение
Время, за которое бегун пробегает
дистанцию, равно ![]() где
где ![]() – время разгона, a – ускорение бегуна, t0
– время движения с постоянной скоростью. За
время разгона бегун пробегает расстояние
– время разгона, a – ускорение бегуна, t0
– время движения с постоянной скоростью. За
время разгона бегун пробегает расстояние
![]()
Поэтому
![]()
где s – длина дистанции. Таким образом,
![]()
По условию задачи, ![]() 1 =
1 = ![]() 2, откуда следует, что
2, откуда следует, что
![]() или
или ![]()
(индексы относятся к обоим бегунам). Отсюда
![]()
Разность длин дистанции s2 – s1
равна разности длин окружностей радиусами R + d и R,
т.е. s2 – s1 = 2![]() d.
d.
Окончательно: ![]()
2 Беговые
дорожки легкоатлетического стадиона состоят из
двух прямолинейных участков, соединённых двумя
полуокружностями. Ширина дорожки d = 1 м. Линия
старта проведена перпендикулярно
прямолинейному участку дорожек и совпадает с
линией финиша. Два бегуна, находящиеся на первой
(внутренней) и второй дорожках, одновременно
принимают старт и пробегают до финиша один круг.
Они разгоняются равноускоренно, пока не наберут
максимальную скорость ![]() 0 = 8 м/с, одинаковую для обоих
бегунов, с которой и пробегают, каждый по
середине своей дорожки, оставшуюся часть
дистанции, финишируя одновременно. Чему равно
отношение n времени разгона второго бегуна ко
времени разгона первого, если полная длина
первой дорожки s1 = 400 м, а время, за которое
спортсмены пробегают всю дистанцию,
0 = 8 м/с, одинаковую для обоих
бегунов, с которой и пробегают, каждый по
середине своей дорожки, оставшуюся часть
дистанции, финишируя одновременно. Чему равно
отношение n времени разгона второго бегуна ко
времени разгона первого, если полная длина
первой дорожки s1 = 400 м, а время, за которое
спортсмены пробегают всю дистанцию, ![]() = 52 с?
= 52 с?
Решение
Используя решение задачи 1, находим,
что время ![]() , за
которое бегун пробегает дистанцию длиной s, равно
, за
которое бегун пробегает дистанцию длиной s, равно
![]()
где a – ускорение бегуна. Отсюда ![]()
Поскольку скорость равномерного
движения обоих бегунов одинакова, времена
разгона бегунов обратно пропорциональны их
ускорениям. Следовательно, искомая величина
равна ![]() (индексы
относятся к обоим бегунам). Имеем
(индексы
относятся к обоим бегунам). Имеем
![]()
Разность длин дистанции бегунов равна
s2 – s1 = 2![]() d (см. решение задачи 1).
d (см. решение задачи 1).
Тогда ![]()
3 Две пружины, соединённые, как показано на рисунке, имеют жёсткости k1 = 15 Н/м и k2 = 10 Н/м. Пружины растянули за свободные концы в разные стороны, совершив работу A = 1 Дж. Каковы потенциальные энергии E1 и E2 деформации каждой из пружин по отдельности?
![]()
Решение
При растяжении пружин, соединённых последовательно, возникающие в них силы упругости одинаковы. Следовательно,
![]()
где ![]() l1
и
l1
и ![]() l2 –
абсолютные удлинения пружин. Их сумма равна
общему удлинению системы:
l2 –
абсолютные удлинения пружин. Их сумма равна
общему удлинению системы: ![]() l1 +
l1 + ![]() l2 =
l2 = ![]() l. Отсюда
l. Отсюда
![]()
С другой стороны, жёсткость двух
пружин, соединённых последовательно, равна ![]() Поэтому работа
по их растяжению есть
Поэтому работа
по их растяжению есть 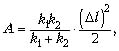 откуда
откуда 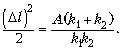
Потенциальные энергии деформации пружин
![]()
Объединяя записанные выражения, получаем ответ:
![]()
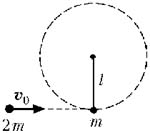
4 Шарик массой m
подвешен на невесомой нерастяжимой нити длиной l
= 1 м. В него ударяется шарик массой 2m, летящий в
плоскости рисунка со скоростью v0 так, что
вектор скорости направлен горизонтально вдоль
линии, соединяющей центры шаров. Какой должна
быть минимальная скорость ![]() 0, чтобы после удара шарик массой
m совершил полный оборот по окружности в
вертикальной плоскости? Удар считать абсолютно
упругим, силы трения не учитывать. Ускорение
свободного падения g = 9,8 м/с2.
0, чтобы после удара шарик массой
m совершил полный оборот по окружности в
вертикальной плоскости? Удар считать абсолютно
упругим, силы трения не учитывать. Ускорение
свободного падения g = 9,8 м/с2.
Решение
Из условия задачи следует, что при
соударении шариков сохраняется проекция
импульса на горизонтальное направление и
кинетическая энергия системы. Обозначив через ![]() 1 и
1 и ![]() 2 скорости шариков m
и 2m после удара, имеем:
2 скорости шариков m
и 2m после удара, имеем:
![]()
Так как сила натяжения нити T работу не совершает, при движении шарика m после удара сохраняется его полная механическая энергия. Для нижней и верхней точек окружности, по которой движется этот шарик, получаем
![]()
где u – скорость шарика в верхней точке. Уравнение движения шарика в верхней точке окружности имеет вид
![]()
Отсюда следует, что скорость u минимальна, если натяжение нити в верхней точке обращается в нуль, т.е.
![]()
Объединяя записанные выражения, получаем ответ:
![]()