S (площадь сечения) 
(скорость
фононов). Заметим, что скорость фононов – это
скорость звука, которая в большинстве твёрдых
тел составляет несколько тысяч метров в секунду. Продолжение. См. № 2/05
Подробнее рассмотрим, каким образом
тепловая энергия переносится фононами вдоль
стержня (рис. 8-4). Пусть тепло переносится слева
направо, т.е. температура уменьшается, если идти
от левого конца стержня к правому. Проведём три
сечения А, В и С одинаковой площади
поперечного сечения, расположенные на
одинаковых расстояниях друг от друга, равных
длине свободного пробега l. Пусть
температуры стержня в этих сечениях
соответственно Т1, Т и Т2.
В соответствии с выбранным направлением
теплового потока Т1 выше Т, а Т
выше Т2. Фононы в сечении А имеют
энергию Е (Т1) на 1 см3,
энергию теплового движения при температуре Т1.
В среднем половина из них перемещается вправо и,
прежде чем столкнуться с другими фононами,
достигает сечения В. Какую энергию
переносят эти фононы каждую секунду в сечение В?
Сначала решим такую задачу: я стою на обочине
шоссе и смотрю на пролетающие мимо автомобили.
Каждый из них движется со скоростью 100 км/ч, на
каждом километре шоссе находится 10 автомобилей.
Сколько автомобилей я насчитаю за час? Ответ: 10
автомобилей в час умножаем на 100 км/ч и получаем
1000 автомобилей. Аналогично тепловая энергия,
переносимая в каждую секунду через сечение В,
равна 0,5Е(Т1) S (площадь сечения) (скорость
фононов). Заметим, что скорость фононов – это
скорость звука, которая в большинстве твёрдых
тел составляет несколько тысяч метров в секунду.
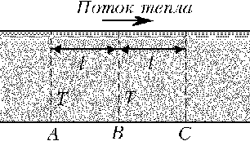
Рис. 8-4. Поперечные сечения стержня А, В и С, по которому распространяется тепловой поток, имеют одну и ту же площадь и расположены на одном и том же расстоянии друг от друга, равном длине свободного пробега l. Их температуры соответственно Т1, Т и Т2, причём Т1 – наивысшая, а Т2 – наинизшая
Через сечение В имеется и поток
фононов влево. Эти фононы следуют из сечения С
и обладают энергией Е (Т2)/см3.
Они несут слева энергию 0,5Е(Т2) S (площадь
сечения) (скорость фононов). Суммарная
энергия Qр, ежесекундно переносимая
через сечение В, равна разности энергий,
поступающих слева и справа:
Qр (суммарная тепловая
энергия за секунду) = 0,5 [Е(Т1) – Е(Т2)]
S.
Немного займёмся арифметикой, чтобы привести формулу для Qр к форме, которая покажет, как можно связать Qр с удельной теплоёмкостью и средней длиной свободного пробега, характеризующими свойства фононов в веществе. Умножим Qр на два числа, равные единице, так что в результате получим то же Qp:
Заметим, что Qp содержит множитель [Е(Т1) – Е(Т2)], представляющий просто разность тепловых энергий в 1 см3 в единицу времени при температурах Т1 и Т2. Эта разность, делённая на разность самих температур, равна удельной теплоёмкости вещества, иначе – той энергии, которую нужно затратить, чтобы повысить температуру 1 см3 вещества на один градус. Как и ранее, обозначим эту величину сp:
Температура стержня уменьшается вдоль длины 2l от значения Т1 до значения Т2. Величина (Т1 – Т2)/2l (которую мы обозначим R) равна скорости изменения или градиенту температуры вдоль стержня. Теперь можно записать количество тепловой энергии, проходящей вдоль стержня за 1 с:
До сих пор мы предполагали, что все фононы распространяются либо влево, либо вправо вдоль стержня. На самом деле, конечно, они распространяются во всех направлениях. Если принять это во внимание, то формула для Qp изменится:
что можно записать в виде
Qp = KрSR.
Здесь Kр обозначает
величину cрl/3, которая зависит
исключительно от свойств вещества: от удельной
теплоёмкости cр фононов, от их
скорости и длины свободного пробега l. Индекс
«р» напоминает, что теплота переносится за
счет колебаний решётки, т.е. за счёт фононов.
Величина Kр называется решёточной
теплопроводностью вещества. Чем эта величина
больше, тем лучше распространяется тепло в
веществе.
Представленная картина распространения тепла вдоль стержня позволяет понять упомянутые ранее в разделе 1 свойства теплопроводности: чтобы возник поток тепла вдоль стержня, необходима разность температур его концов; тепло вдоль стержня распространяется довольно медленно. Приведённая выше формула для Qp показывает, что, когда R равно нулю, т.е. нет разности температур, поток тепла тоже равен нулю. Довольно медленное распространение тепла вдоль серебряной ложки, опущенной в стакан с горячим кофе, объясняется соударениями фононов, которые они испытывают при распространении вдоль ложки, т.к. длина их свободного пробега много меньше длины ложки. Если стержень представляет собой цельный кристалл и охлаждён до температуры, близкой к абсолютному нулю, то средняя длина свободного пробега фононов становится очень большой. Тепловой импульс, подведённый к одному концу такого стержня, будет распространяться в нём со скоростью, сравнимой со скоростью звука в веществе. Тогда говорят, что тепловая энергия переносится вторым звуком.
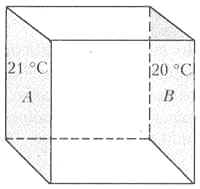
Рис. 8-5. Куб из вещества, используемый для определения теплопроводности. Длина сторон куба равна 1 см, а температура противоположных граней А и В равна 21 °С и 20 °С соответственно
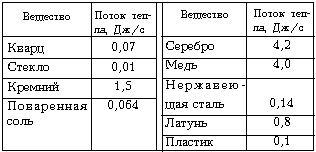
Рассмотрим теперь стержень, имеющий форму куба, длина ребёр которого равна 1 см3 (рис. 8-5). Обкладывая куб соответствующим образом нагретыми пластинами, можно добиться того, что грани А и В будут удерживаться при температурах 21 °С и 20 °С соответственно. Сечение стержня 1 см2, а градиент температуры 1 °С/см. Из приведённой выше формулы для Qpр видно, что количество тепла, перетекающего за 1 с от грани А к грани В, равно как раз Kр. Таким образом, теплопроводность, как мы её определили выше, равна тепловой энергии, перетекающей за 1 с между двумя противоположными гранями куба со стороной 1 см, когда разность температур между гранями равна 1 °С. В табл. 8-3 приведена эта величина в Дж/с для различных веществ в форме такого куба. Джоуль – единица количества тепловой энергии. Если сообщить 1 см3 воды тепловую энергию 1 Дж, его температура повысится почти на четверть градуса Цельсия.
Числа в табл. 8-3 указывают на интересные закономерности. Металлы типа меди и латуни проводят тепло лучше, чем диэлектрики типа стекла и пластика, а чистые металлы, например медь, проводят тепло лучше, чем сплавы, как, например, латунь, сплав меди и цинка. Главная причина, почему металлы проводят тепло лучше, чем кристаллические диэлектрики при тех же условиях, состоит в том, что в дополнение к фононам, имеющимся в обоих случаях, у металлов есть ещё свободные электроны, покинувшие внешние оболочки атомов. Эти электроны могут двигаться внутри вещества и давать дополнительный вклад в поток тепловой энергии. Электронную часть теплопроводности металлов мы рассмотрим в следующем разделе и тогда поймём, почему сплавы проводят тепло хуже, чем чистые металлы.
Таблица 8-3. Поток тепла в секунду через куб, показанный на рис. 8-5
Почти вся тепловая энергия в диэлектриках и полупроводниках сосредоточена в фононах. В металлах же тепловая энергия содержится не только в фононах, но и в парах электрон–дырка, возникающих вблизи ферми-поверхности за счёт температуры (см. гл. 6). Таким образом, поток тепла в металле обусловлен не только фононами, но также электронами и дырками.
Тепловая энергия переносится
электронами и дырками, совершенно так же, как и
фононами. Можно использовать формулу для
теплопроводности фононов, подставив
соответствующие величины для электронов и дырок:
удельную теплоёмкость се, скорость Ферми F и
среднюю длину свободного пробега для электронов le.
Обозначая электронную теплопроводность Ke,
получим:
Таким образом, электроны и дырки за 1 с переносят тепловую энергию Qe = KeSR, а полная тепловая энергия Q = Qe + Qр. Заметим, что в каждом случае тепловая энергия определяется произведением удельной теплоёмкости, скорости и средней длины свободного пробега.
Оценим теперь относительную величину вклада электронов и фононов в теплопроводность. Сначала рассмотрим средние длины свободного пробега. Элекрон или дырка сталкиваются с фононом намного раньше того, как они столкнутся с другим электроном или дыркой. Для фононов тоже наиболее вероятны столкновения с другими фононами. Поэтому средние длины свободного пробега во всех случаях примерно одинаковы, что можно видеть из табл. 8-2. Хотя электронная удельная теплоёмкость меньше, чем фононная, скорость Ферми много больше скорости звука в веществе. В результате теплопроводность за счёт электронов и дырок сравнима или даже больше теплопроводности за счёт фононов.
В решётке сплава более одного типа атомов, например, атомы меди и цинка в латуни. Это означает, что теряется трансляционная симметрия чистого металла, в котором каждый узел решётки занят атомом одного сорта. Такое отклонение от идеальности проявляется как возмущение, действующее на частицы (электроны, дырки или фононы) в их квантовых состояниях. Откликом на это возмущение является переход в другое квантовое состояние, что является просто иной формой утверждения, что частица испытала столкновение. Это дополнительное рассеяние частиц означает, что в сплавах теплопроводность уменьшается.
Из табл. 8-3 следует, что кварц намного лучше проводит тепло, чем стекло, несмотря на то, что оба вещества состоят из диоксида кремния. Таким образом, средняя длина свободного пробега для фононов в стекле должна быть меньше, чем в кварце. Разница между двумя веществами состоит в том, что кварц – кристалл, его молекулы упорядочены и обладают трансляционной симметрией. В стекле этой симметрии нет. Таким образом, мы приходим к общему выводу, что потеря трансляционной симметрии, происходит ли она из-за образования сплава или из-за превращения кварца в стекло, приводит к уменьшению средних длин свободного пробега фононов и электронов. В конечном итоге теплопроводность уменьшается.
Когда хозяйка не в силах открутить металлическую крышку стеклянной бутылки, она прибегает к старому способу – нагревает крышку, например, подставляя её под струю горячей воды. В некоторых случаях это помогает, и крышка легко откручивается. Конечно, одной из причин этого явления является то, что горячая вода растворила засохшее вокруг горлышка содержимое бутылки. Но этот метод работает и тогда, когда бутылка чиста. Причина в том, что нагревание расширяет крышку, так что она уже не так плотно прилегает к бутылке. Такое изменение размеров куска вещества при изменении температуры называется тепловым расширением. Практически во всех ситуациях, с которыми мы обычно сталкиваемся, это расширение необычайно мало и не заметно невооружённым глазом. В табл. 8-4 приведены значения величины теплового расширения для ряда обычных веществ.
Таблица 8-4. Удлинение стержня длиной 1 см при повышении температуры от 0 до 100 °С
Как видно, разные металлы расширяются по-разному при одинаковом повышении температуры, а стекло расширяется меньше. Ясно, почему удаётся открутить металлическую крышку после нагревания, несмотря на то, что стекло также нагревается.
Что заставляет твёрдое тело расширяться при нагревании? Рассмотрим простой пример, когда происходит нечто похожее, а именно, воздушный шарик, наполненный газом (рис. 8-6). Давление газа, стремящееся расширить шарик, в точности компенсируется направленным противоположно давлением упругих сил, создаваемых оболочкой шарика и стремящихся его сжать. Баланс сил определяет размер шарика при заданном давлении газа внутри. Если нагреть шарик, давление газа возрастёт, что приведёт к расширению шарика и увеличению противодействующих этому расширению упругих сил, что восстановит баланс. При этом общее количество газа внутри воздушного шарика останется неизменным.
Представим теперь, что мы заменили шарик поверхностью твёрдого тела, а молекулы газа – фононами в этом теле (а также свободными электронами, если речь идёт о металле) (нижняя часть рис. 8-6). Эти фононы и электроны оказывают давление на поверхность, причём давление растёт с повышением температуры. В результате происходит тепловое расширение твёрдого тела.
Всё очень хорошо, но как понять происхождение давления, выразив его через свойства молекул газа или фононов и электронов в твёрдом теле? Рассмотрим сначала газ. На рис. 8-7 показана малая часть поверхности шарика и траектории нескольких молекул, ударяющихся об эту поверхность и отскакивающих от неё. При каждом отскоке молекулы оболочки испытывают определённую отдачу. В данном случае нужно учитывать закон сохранения импульса. Импульс каждой молекулы изменяется в результате соударения со стенкой. Это изменение должно компенсироваться изменением импульса стенки, причём полный импульс остаётся неизменным.
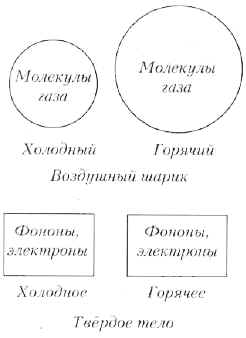
Рис. 8-6. Вверху показано расширение воздушного шарика при нагревании, внизу – расширение твёрдого тела при нагревании. Молекулы газа (фононы, а также электроны, когда речь идёт о металле) внутри шарика (внутри твёрдого тела) оказывают давление на шарик (на поверхность твёрдого тела). Давление растёт с ростом температуры, и шарик (твёрдое тело) немного расширяется
Суммарный эффект таких отдач вследствие соударений молекул с оболочкой состоит в том, что давление газа стремится сдвинуть оболочку вправо. В то же время оболочка испытывает аналогичные соударения с молекулами с другой стороны, и они передают ей импульс, направленный влево. Импульс, и следовательно, давление газа, увеличивается с увеличением скорости молекул, а это происходит при нагревании газа. Итак, мы видим, что при нагревании газа внутри шарика сам шарик расширяется.
Рис. 8-7. Молекулы газа, отскакивая от стенки сосуда (например, оболочки воздушного шарика), передают ему импульс. Величина переданного импульса за 1 с пропорциональна давлению на стенку
Вопрос. В какой же момент начинает играть роль упругость шарика?
Ответ. Дополнительное давление нагретого газа внутри шарика по сравнению с холодным воздухом снаружи уравновешивается эффективным давлением, направленным внутрь и обусловленным тем, что шарик увеличился в размерах и упругие силы стремятся его сжать. Ситуация напоминает растягивание пружины, которая стремится вернуться к исходному размеру.
Свободные электроны в металле, в основном ответственные за его теплопроводность, движутся внутри металла, но не могут выскочить из него через поверхность. Притяжение отрицательно заряженных электронов к положительно заряженным ионам удерживает элеткроны внутри металла. Влияние этого притяжения можно представить, вообразив непроницаемую, но упругую оболочку вокруг куска металла. Электроны заперты в этой оболочке, но непрерывно налетают на неё и отражаются назад, аналогично тому, как это происходит с молекулами газа в шарике. В результате на поверхность металла изнутри действует создаваемое электронами давление. Средняя скорость электронов увеличивается с ростом температуры, давление тоже увеличивается, и металл расширяется. Этот эффект называется электронным вкладом в тепловое расширение.
Что можно сказать о фононах? У электронов есть масса и они движутся с разными скоростями. Нетрудно представить, что при соударении со стенкой они передают ей некоторый импульс. Для фононов картина иная. Они являются квантами энергии колеблющихся атомов, причём нет очевидных способов приписать фононам какую-то массу. У фонона нет импульса в том смысле, как у молекулы. Это становится понятным, если вспомнить, что фонон есть квантовое понятие, связанное с звуковой волной в твёрдом теле. Для каждого атома в звуковой волне с данной скоростью в определённом направлении найдётся другой атом, имеющий ту же скорость, но в противоположном направлении, так что полный импульс звуковой волны равен нулю. Мы не можем говорить о столкновении фонона с поверхностью твёрдого тела с передачей импульса.
Однако есть иной способ взглянуть на происходящее, который придаёт смысл идее давления, обусловленного фононами. Начнём с того, что частота, а следовательно, энергия, фонона уменьшается с увеличением объёма кристалла. Если ничто не удерживает отдельные части кристалла вместе, это означает, что даже при постоянной температуре кристалл будет стремиться расширяться, т.к. тогда его энергия, связанная с фононами, будет уменьшаться. Можно интерпретировать это как наличие давления фононов, расширяющее кристалл. Конечно, реальный кристалл так себя не ведёт, потому что в нём есть внутренние силы, связанные с заряженными ядрами и электронами, которые удерживают его от развала. Но если немного нагреть кристалл, распределение фононов по разным квантовым уровням энергии изменится, следовательно, изменится и давление фононов. Это приведёт к изменению объёма всего кристалла.
Такой способ связи теплового расширения с изменением энергетических уровней за счёт изменения объёма является примером того, как квантовая механика объединяется со статистической физикой.